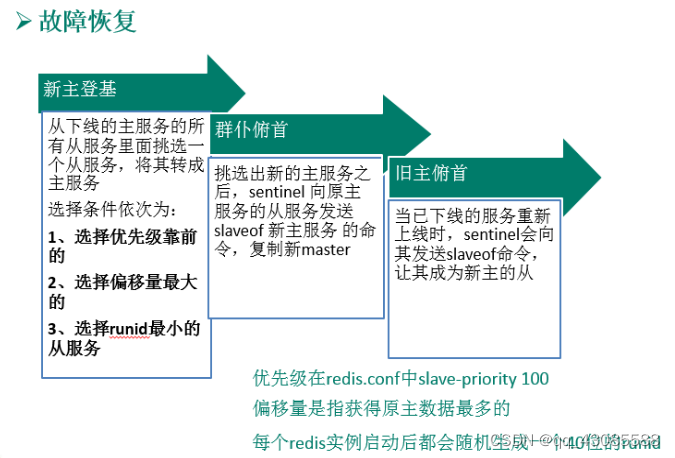
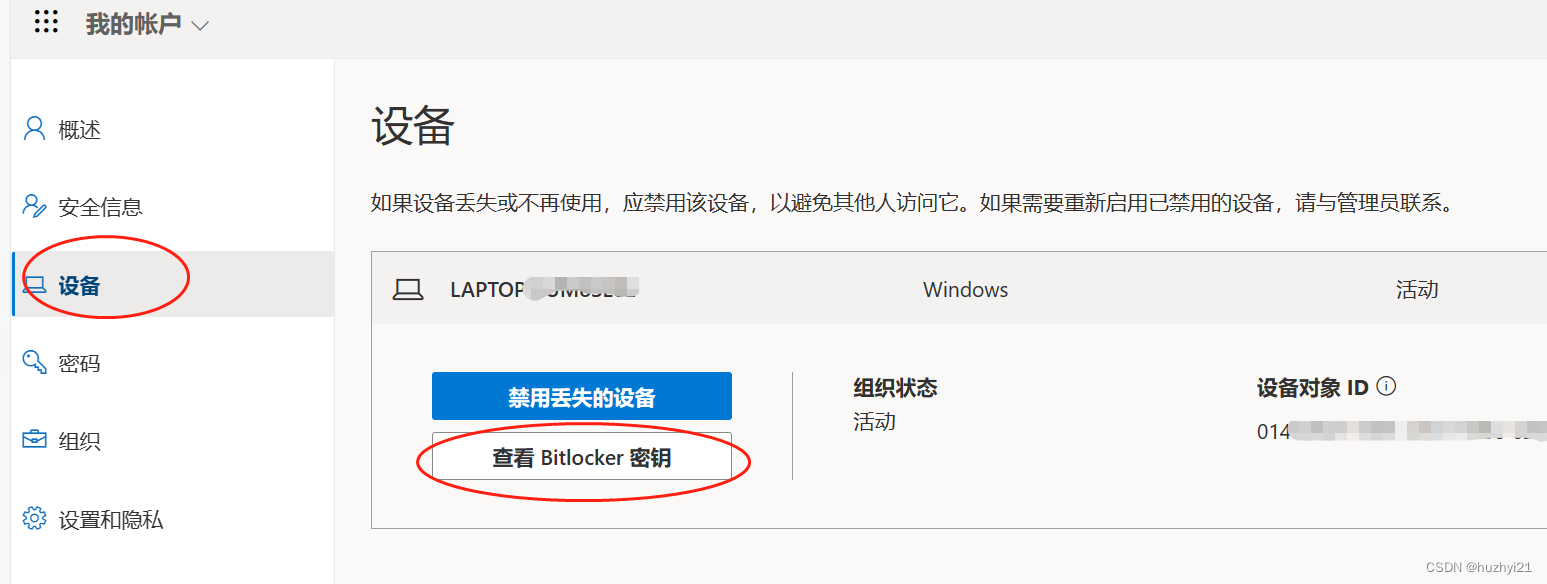
对于像我一样喜欢跳跃着学习的聪明人来说，肯定要学springboot，什么sevlet、maven、java基础，都太老土了，用不到就不学。所以古代的聪明人有句话叫“书到用时方恨少”，测试开源项目时，编译总是报错，不是缺依赖就是少java类，pom中除了会填依赖项，其他全都看不懂，项目跑不起来就得赶紧找老师补习maven。

有一个困扰已久的问题，都快遗忘了，看反编译的java项目时，jar包里的路径是按什么结构生成的？学了maven教程，仔细对比源码路径和jar包里的目录结构，发现我把groupId、package和源码路径混为一谈了。

1、package 包名和groupId可以不一致，groupId是maven引入依赖时检索的名称，package 包名是java程序中import的名称。两者作用域不同，groupId是maven定义的，package 是java定义的。 2、默认情况下源码的路径与包名相同，打包后的路径项目与源码的路径相同 但是如果源码的路径与包名不同，打包后的路径以包名为准，与源码路径不同

p01-maven-java-1.0-SNAPSHOT.jar中的路径：

源码的路径:

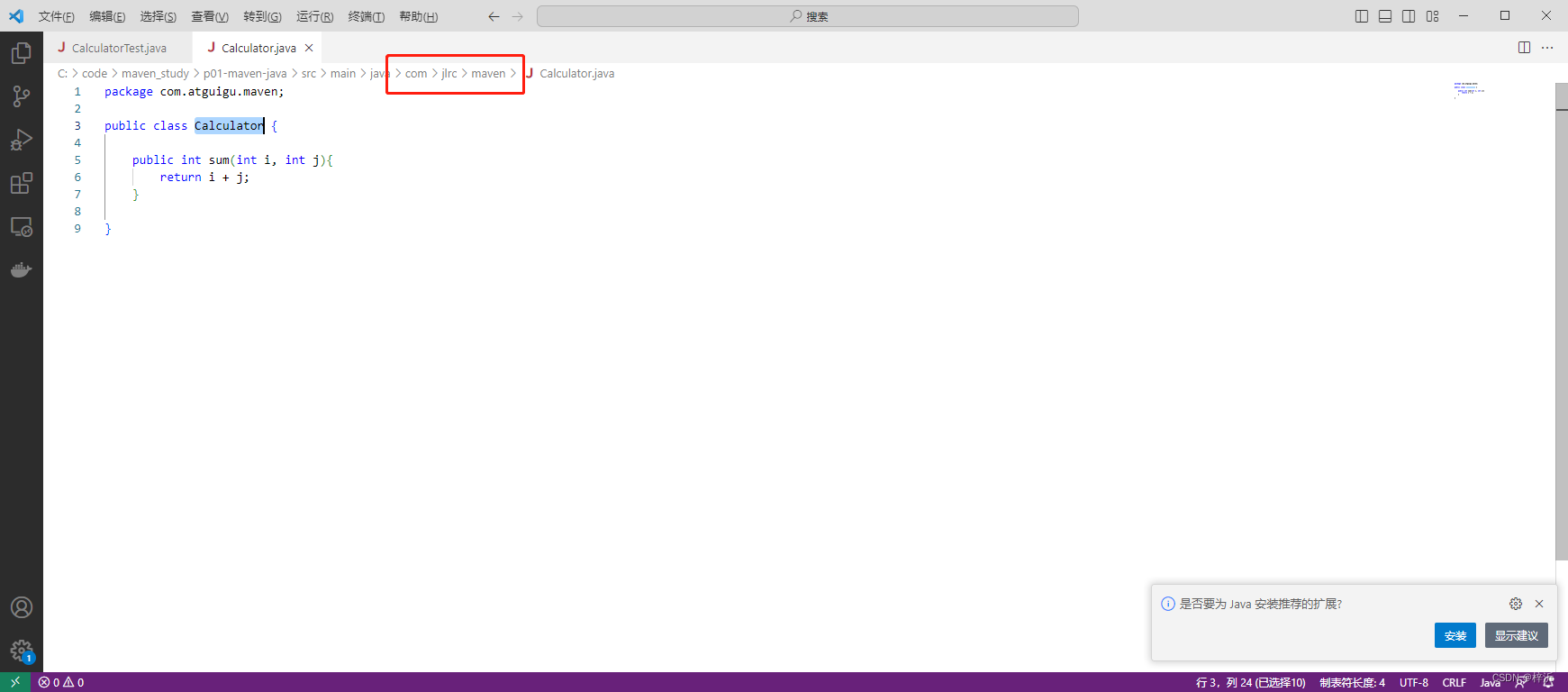
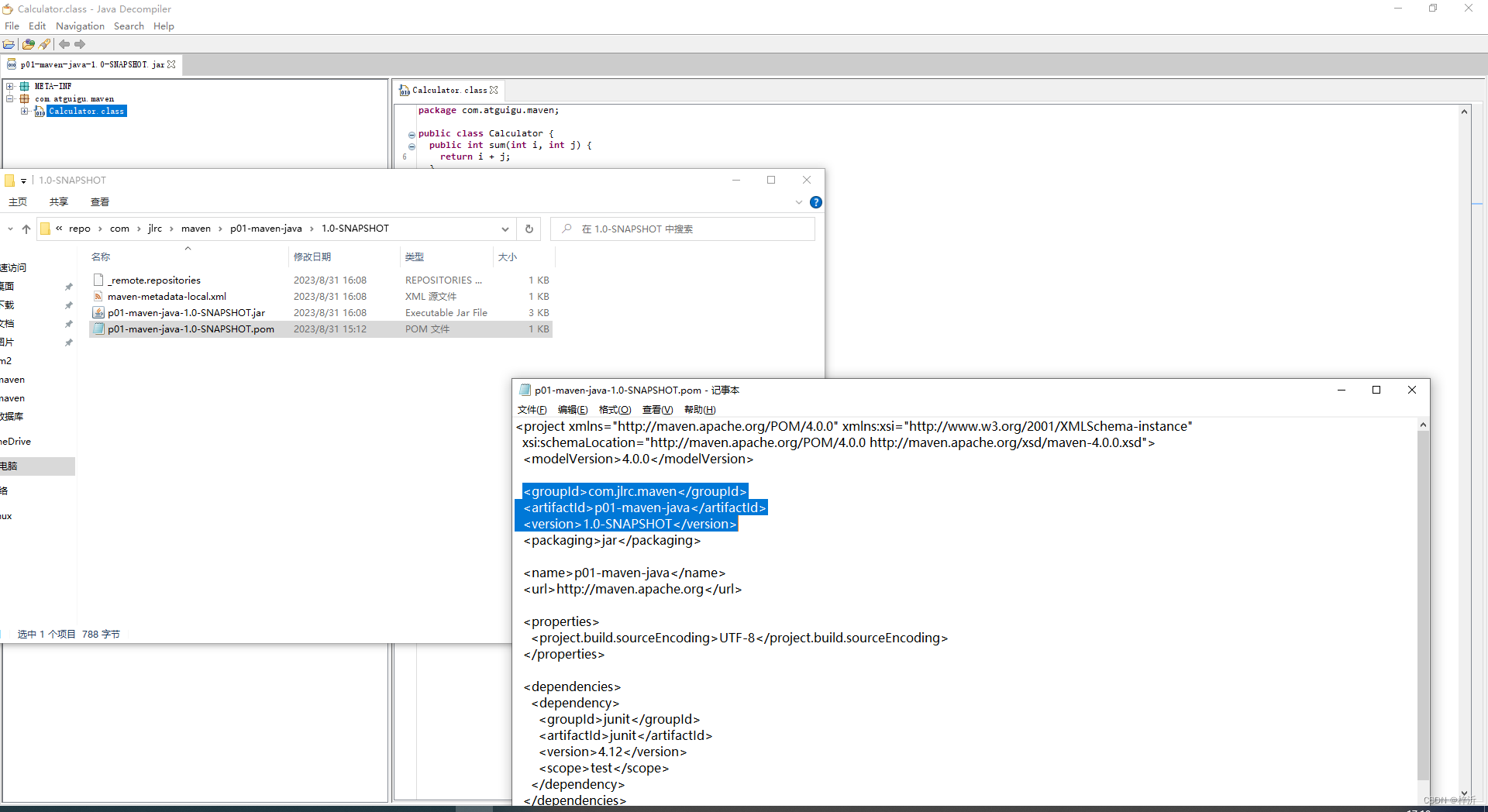
//Calculator.java中的包名是 package com.atguigu.maven;

package com.atguigu.maven;public class Calculator {public int sum(int i, int j){return i + j;}}

//p01-maven-java-1.0-SNAPSHOT.pom中的groupId是com.jlrc.maven

<groupId>com.jlrc.maven</groupId>
<artifactId>p01-maven-java</artifactId>
<version>1.0-SNAPSHOT</version>

编译打包后，Calculator类在jar包中的路径是com.atguigu.maven

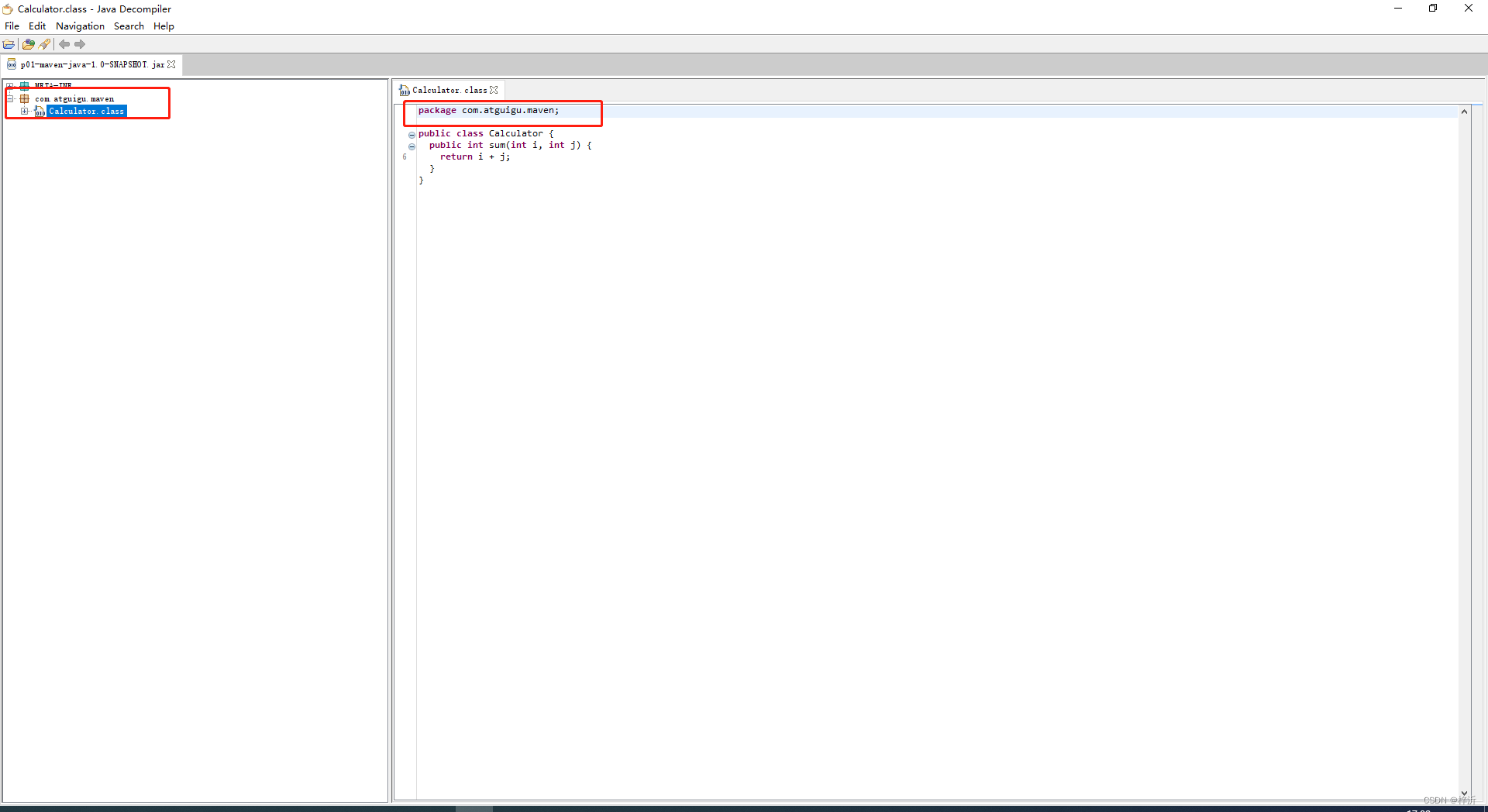
源码文件Calculator.java的路径是p01-maven-java\src\main\java\com\jlrc\maven

可用看出打包后包中类的路径是由package com.atguigu.maven;决定的，

而maven仓库中包存放的路径是由pom文件中的groupId\artifactId\version决定的。

只不过一般情况下，groupId、package和源码路径都设置成一样的，在idea创建maven项目时groupId和package的默认设置就是相同的，而且自动创建的源码路径和package一样，所以平时没发现他们的区别。

尚硅谷Maven教程（maven入门+高深，全网无出其右！）_哔哩哔哩_bilibili