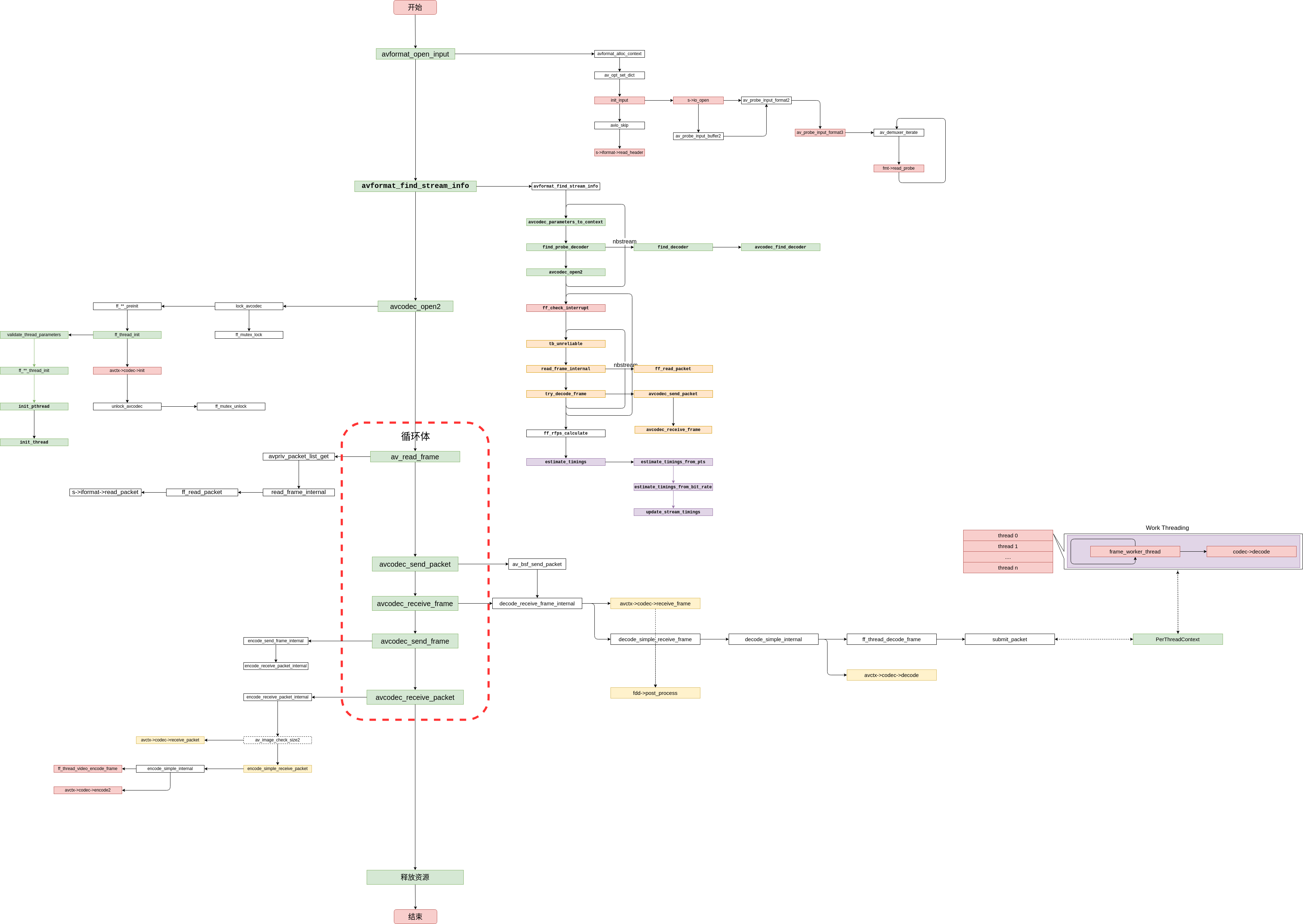
文章目录
- 图的邻接矩阵
- 一.Floyd-Warshall算法思想(基于动态规划)
- 二.Floyd-Warshall算法接口
- 笔记附录:单源最短路径--Bellman-Ford算法
- 1.Bellman-Ford算法接口核心部分
- 2.Bellman-Ford算法接口
图的邻接矩阵
namespace Graph_Structure
{//Vertex是代表顶点的数据类型,Weight是边的权值的数据类型,MAX_W是权值的上限值(表示不相两)//Direction表示图是否为有向图template<class Vertex, class Weight = int, Weight MAX_W = INT_MAX, bool Direction = false>class Graph{typedef Graph<Vertex, Weight, MAX_W, Direction> Self;public://使用编译器的默认构造函数Graph() = default;//给定一个存放顶点的数组用来初始化图Graph(const Vertex* a, size_t n){_vertexs.reserve(n);_indexMap.rehash(n);_matrix.resize(n, std::vector<Weight>(n, MAX_W));for (size_t i = 0; i < n; ++i){_vertexs.push_back(a[i]);//建立顶点和数组下标的映射(目的是为了邻接矩阵的边存储)_indexMap[a[i]] = i;}}//获取顶点在邻接矩阵中对应的下标size_t GetVertexIndex(const Vertex& vertex){if (_indexMap.find(vertex) == _indexMap.end()){throw "invalued_para";return -1;}return _indexMap[vertex];}void _AddEdge(size_t srci, size_t dsti, const Weight& w){//判断是有向图还是无向图if (Direction == false){_matrix[dsti][srci] = w;}_matrix[srci][dsti] = w;}//给定起点和终点,在邻接矩阵中添加一条边void AddEdge(const Vertex& src, const Vertex& dst, const Weight& w){if (_indexMap.find(src) == _indexMap.end() || _indexMap.find(dst) == _indexMap.end()){throw "invalued_para";}size_t srci_index = GetVertexIndex(src);size_t dst_index = GetVertexIndex(dst);_AddEdge(srci_index, dst_index, w);}//将图的邻接矩阵打印出来void Print(){for (auto e : _vertexs){std::cout << e << '[' << _indexMap[e] << ']' << std::endl;}std::cout << " ";for (int i = 0; i < _vertexs.size(); ++i){std::cout << i << " ";}std::cout << std::endl;int i = 0;for (auto arry : _matrix){std::cout << i++ << ' ';for (auto e : arry){if (e == MAX_W){printf("%4c ", '*');}else{printf("%4d ", e);}}std::cout << std::endl;}}//图的广度优先遍历void BFS(const Vertex& src){size_t begin = GetVertexIndex(src);std::queue<int> QNode;std::vector<bool> Label(_vertexs.size(), false);QNode.push(begin);Label[begin] = true;size_t Level = 0;while (!QNode.empty()){size_t LevelSize = QNode.size();for (size_t i = 0; i < LevelSize; ++i){size_t front = QNode.front();QNode.pop();std::cout << _vertexs[front] << '[' << front << ']' << std::endl;for (int j = 0; j < _vertexs.size(); ++j){if (Label[j] == false && _matrix[front][j] != MAX_W){QNode.push(j);Label[j] = true;}}}}}//图的深度优先遍历void DFS(const Vertex& src){std::vector<bool> visited(_vertexs.size(), false);_DFS(GetVertexIndex(src), visited);}private:void _DFS(size_t srci, std::vector<bool>& visited){visited[srci] = true;std::cout << _vertexs[srci] << '[' << srci << ']' << std::endl;for (int i = 0; i < _vertexs.size(); ++i){if (_matrix[srci][i] != MAX_W && visited[i] == false){_DFS(i, visited);}}}private:std::vector<Vertex> _vertexs; // 顶点集合std::unordered_map<Vertex, size_t> _indexMap; // 顶点映射下标std::vector<std::vector<Weight>> _matrix; // 邻接矩阵};
}在有向赋权图中(可以存在带负权值的路径,但不能存在总权值为负数的环路),Floyd-Warshall算法可以求出任意两个顶点间的最短路径
一.Floyd-Warshall算法思想(基于动态规划)
-
假设图中有
N个顶点,顶点按照0~N-1进行编号 -
算法中使用二维数组
Dist来记录点与点之间的最短路径长度,Dist[i][j]表示第i个顶点到第j个顶点的最短路径长度,Dist数组的初始状态为图的邻接矩阵的拷贝 -
任意两个顶点
i和j之间的最短路径上可能存在0 ~ N-2个顶点: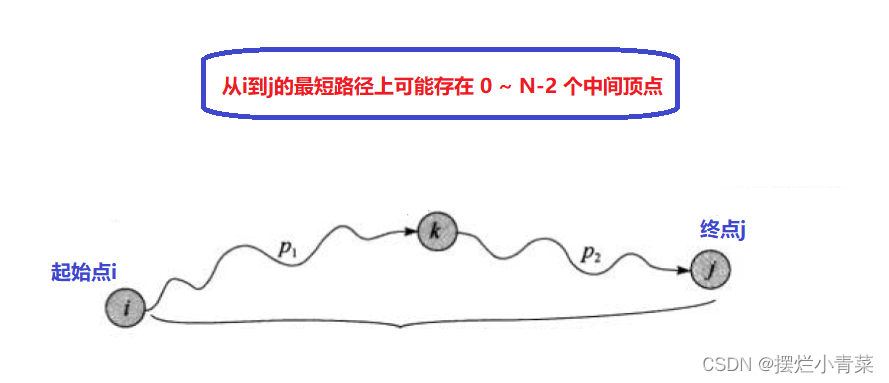
-
假设顶点
i到顶点j的最短路径上编号最大的顶点为k顶点,i到k之间的路径为p1,k到j之间的路径为p2(不难证明,p1同时也是顶点i到顶点k的最短路径,p2同时也是顶点k到顶点j的最短路径) -
从而有状态转移方程:
Dist[i][j] = Dist[i][k] + Dist[k][j]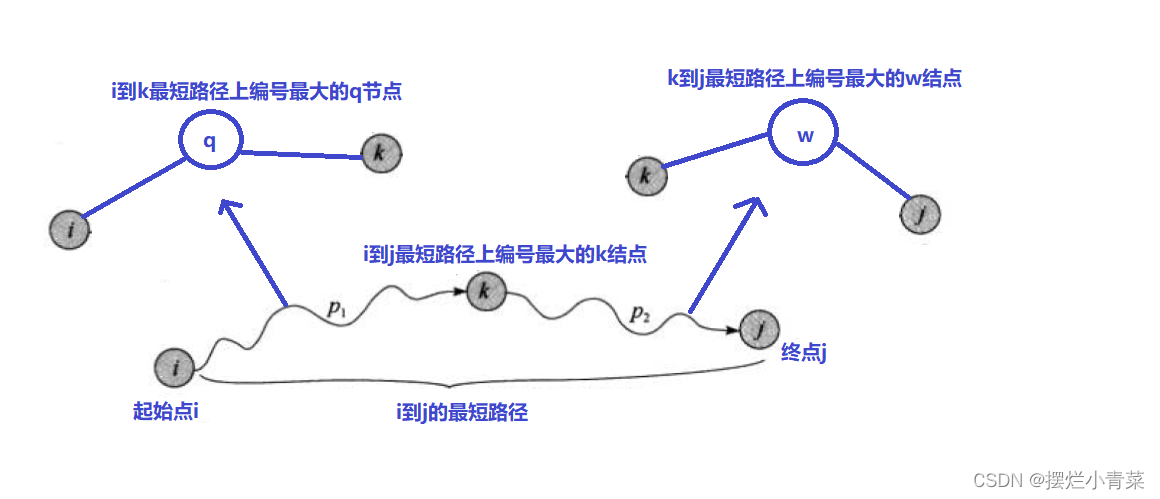
-
最短路径
p1和p2也可以按照相同的方式划分出子路径.重复路径划分,直到将路径划分成不能再被分割的各个最小状态,从各个最小状态开始进行状态转移就可以得到顶点i到顶点j的最短路径. -
状态转移求任意两点的最短路径的过程可以通过如下循环完成:
//动态规划求最优解for (int k = 0; k < _vertexs.size(); ++k){for (int i = 0; i < _vertexs.size(); ++i){for (int j = 0; j < _vertexs.size(); ++j){if (Dist[i][k] != MAX_W && Dist[k][j] != MAX_W &&Dist[i][k] + Dist[k][j] < Dist[i][j]){Dist[i][j] = Dist[i][k] + Dist[k][j];}}}}

- 其他任意两点的最短路径的确定过程也是类似的
二.Floyd-Warshall算法接口
//多源最短路径算法(允许带负权路径存在)//Dist数组用于记录顶点间的最短路径的长度//ParentPath数组用于记录最短路径上某个顶点的前驱结点编号void FloydWarShall(std::vector<std::vector<Weight>>& Dist, std::vector<std::vector<int>>& ParentPath){Dist.resize(_vertexs.size(), std::vector<Weight>(_vertexs.size(), MAX_W));ParentPath.resize(_vertexs.size(), std::vector<int>(_vertexs.size(), -1));//根据图的邻接矩阵初始化Dist数组for (int i = 0; i < _matrix.size(); ++i){for (int j = 0; j < _matrix.size(); ++j){if (i == j){Dist[i][j] = 0;}else if(_matrix[i][j] != MAX_W){Dist[i][j] = _matrix[i][j];ParentPath[i][j] = i;}}}//动态规划求各个最短路径for (int k = 0; k < _vertexs.size(); ++k){for (int i = 0; i < _vertexs.size(); ++i){for (int j = 0; j < _vertexs.size(); ++j){if (Dist[i][k] != MAX_W && Dist[k][j] != MAX_W &&Dist[i][k] + Dist[k][j] < Dist[i][j]){Dist[i][j] = Dist[i][k] + Dist[k][j];//i到j最短路径上,j顶点的前驱为k到j最短路径上j的前驱ParentPath[i][j] = ParentPath[k][j];}}}}}
笔记附录:单源最短路径–Bellman-Ford算法
Bellman-Ford算法可以在带负权路径的图中求解单源最短路径的问题- 一维数组
Dist用于记录源点到其他顶点的最短路径的长度:Dist[i]表示源点到i号结点的最短路径长度 - 一维数组
ParentPath数组用于记录最短路径上某个顶点的前驱结点编号:ParentPath[i]表示在最短路径上,第i号结点的前驱结点的编号
1.Bellman-Ford算法接口核心部分
for (int i = 0; i < _vertexs.size() - 1; ++i){for (int j = 0; j < _vertexs.size(); ++j){for (int k = 0; k < _vertexs.size(); ++k){if (_matrix[j][k] != MAX_W && dist[j] != MAX_W &&_matrix[j][k] + dist[j] < dist[k]){dist[k] = _matrix[j][k] + dist[j];parentPath[k] = j;}}}
- 可以证明:上面的循环可以遍历任何一条可能存在的最短路径.对于任意一条最短路径,内部的双层循环至少可以记录下最短路径上的一条边,因此最外层循环只要进行
N-1次(N为图的顶点数目)就可以遍历完所有的最短路径:
Bellman-Ford算法需要检验图中是否存在总权值为负数的环路,存在总权值为负数的环路的图无法求解最短路径问题
2.Bellman-Ford算法接口
//带负权路径的单源最短路径算法bool BellmanFord(const Vertex& src, std::vector<Weight>& dist, std::vector<int>& parentPath){dist.resize(_vertexs.size(), MAX_W);parentPath.resize(_vertexs.size(), -1);int srci = GetVertexIndex(src);dist[srci] = Weight();bool flag = true;for (int i = 0; i < _vertexs.size() - 1; ++i){for (int j = 0; j < _vertexs.size(); ++j){for (int k = 0; k < _vertexs.size(); ++k){if (_matrix[j][k] != MAX_W && dist[j] != MAX_W &&_matrix[j][k] + dist[j] < dist[k]){//经过j结点,更新源点到k结点的路径长度dist[k] = _matrix[j][k] + dist[j];parentPath[k] = j;flag = false;}}}if (flag){//路径不再发生更新,则说明所有最短路径都已经确定return false;}flag = true;}//检验图中是否存在负权环路//如果存在负权环路,则Dist数组会继续被更新flag = false;for (int j = 0; j < _vertexs.size(); ++j){for (int k = 0; k < _vertexs.size(); ++k){if (_matrix[j][k] != MAX_W && dist[j] != MAX_W &&_matrix[j][k] + dist[j] < dist[k]){dist[k] = _matrix[j][k] + dist[j];flag = true;}}}return flag;}




![微服务通信[HTTP|RPC同步通信、MQ异步通信]](https://img-blog.csdnimg.cn/5aa453d58d564772a67dc82e6425a370.png)