课程链接：

计算机组成_北京大学_中国大学MOOC(慕课)

3 - 2 - 302-门电路的基本原理（11-'39--）_哔哩哔哩_bilibili

现代计算机的CPU和其他很多功能部件都是基于晶体管的集成电路，想要了解计算机组成的基本原理，还是需要有一些集成电路的基本知识。就让我们从最简单的门电路的实现开始吧。

1. 门电路的基本原理

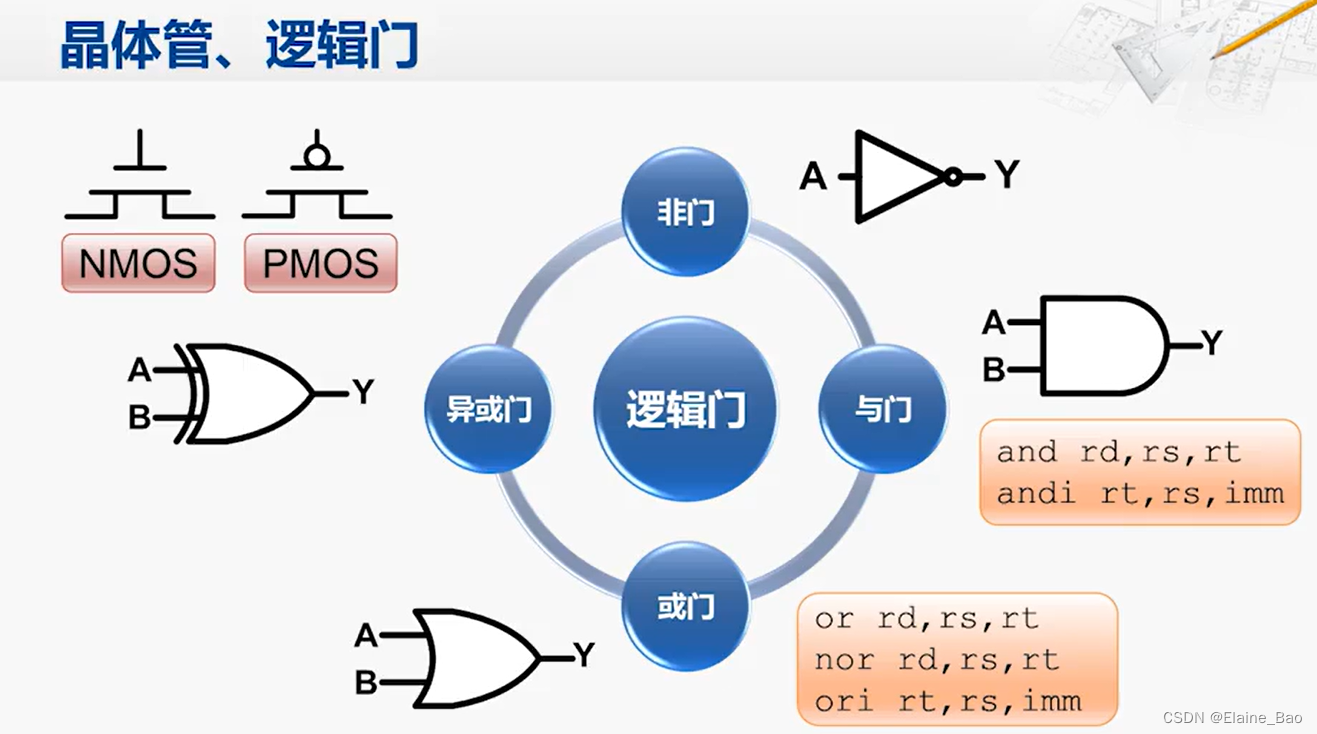
晶体管是构成现代集成电路的基本原件，通常使用的是MOS晶体管，MOS晶体管又主要有2种类型，N型MOS管和P型MOS管。N MOS导通的条件是Gate端连接了高电平，P MOS正好相反，其导通条件是Gate端连接了低电平。这就好比我们有2种类型的水龙头，一种当我们把把手向下压的时候会出水，另一种当我们把把手向上拉的时候会出水。

​

那如何用晶体管构建逻辑门呢？

1. 非门

最简单的一种逻辑是非门，只需要两个晶体管就可以实现。我们来看一下非门是如何工作的，VDD连接的是电源，也就是高电平（1），接地表示低电平（0）。当A为0是，P MOS导通，N MOS不通，此时高电平1传送到Y。当A为1时，P MOS不同，N MOS导通，此时低电平0传送到Y。这样就实现了非门的功能。

​

2. 与门

虽然我们需要的是与门，但实际上与非门比与门的实现更为简单，所以实际用与非门和非门来实现与门。

与非门使用4个晶体管来实现。我们这里来看一下与非门的工作过程。当A=1,B=1时，两个N MOS导通，两个P MOS不通，所以低电平0传送到了Y。当A=1,B=0时或A=0,B=1或A=0,B=0时，两个P MOS中至少有一个导通，所以高电平1传送到了Y。

​

除了非门和与门，其他比较常见的还有或门和异或门。这些逻辑门可以用于实现计算机中所要求的各种逻辑运算，如and, or等。

2. 寄存器的基本原理

在CPU中，用来存储信息的非常重要的部件就是寄存器。比如说0号通用寄存器，在MIPS的体系结构中，是一个32位的寄存器，从电路实现上来说，这32个bit都是一样的，我们来看其中一个，它可以用一个叫做D触发器的部件来实现。

1. D触发器

触发器是一个具有存储信息能力的基本单元，它也是由若干逻辑门构成的，这里我们不深入到它的实现细节，而关注它提供的功能。触发器有很多种类型，D触发器是其中一种。

D触发器有一个数据输入，一个数据输出和一个时钟输入。它的功能表现是这样的：在时钟的上升沿，采样输入D的值，传送到输出Q，其余时间输出Q的值不变。

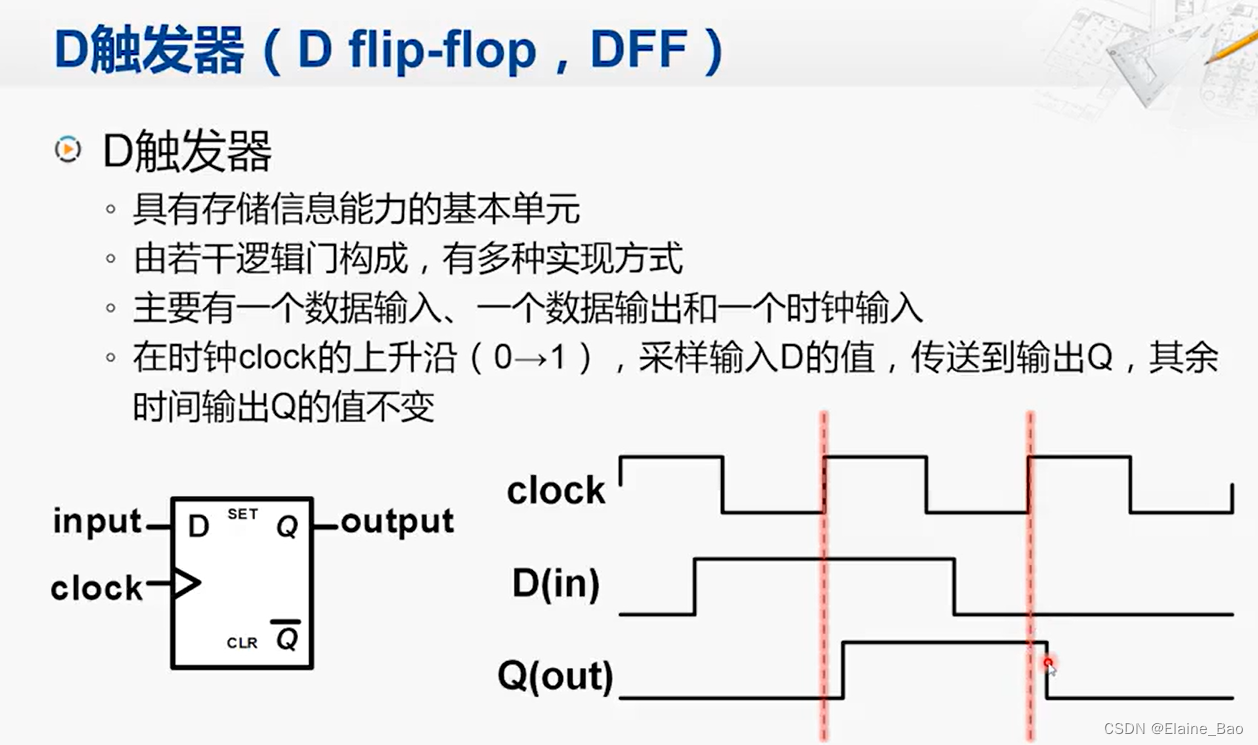
如果我们把32个D触发器组合起来就可以构成一个32位的寄存器，当然这只是一个简单的原理性实现，现实中寄存器的实现要复杂得多。用这样一个32位寄存器，就可以构成CPU中的一个通用寄存器，用同样的方法可以做出其他的通用寄存器以及PC，IR这样的寄存器，再将这样的寄存器与其他由逻辑门构成的电路相连，就构成了我们这个复杂的CPU了。

3. 逻辑运算的实现

现在我们已经掌握了基本的门电路，可以提供简单的逻辑运算，例如与门可以实现2个bit的与操作。但是这和计算机中与运算指令所需要的功能还是有差距的，例如and rd,rs,rt这条指令，它的两个源操作数和目的操作数都是32位的寄存器。那么我们怎么用与门来完成呢？其实也很简单，我们就把32个与门并排连起来，将32位的输入分别连接到这32个与门上，输出再整合到一起变成1个32位的输出。

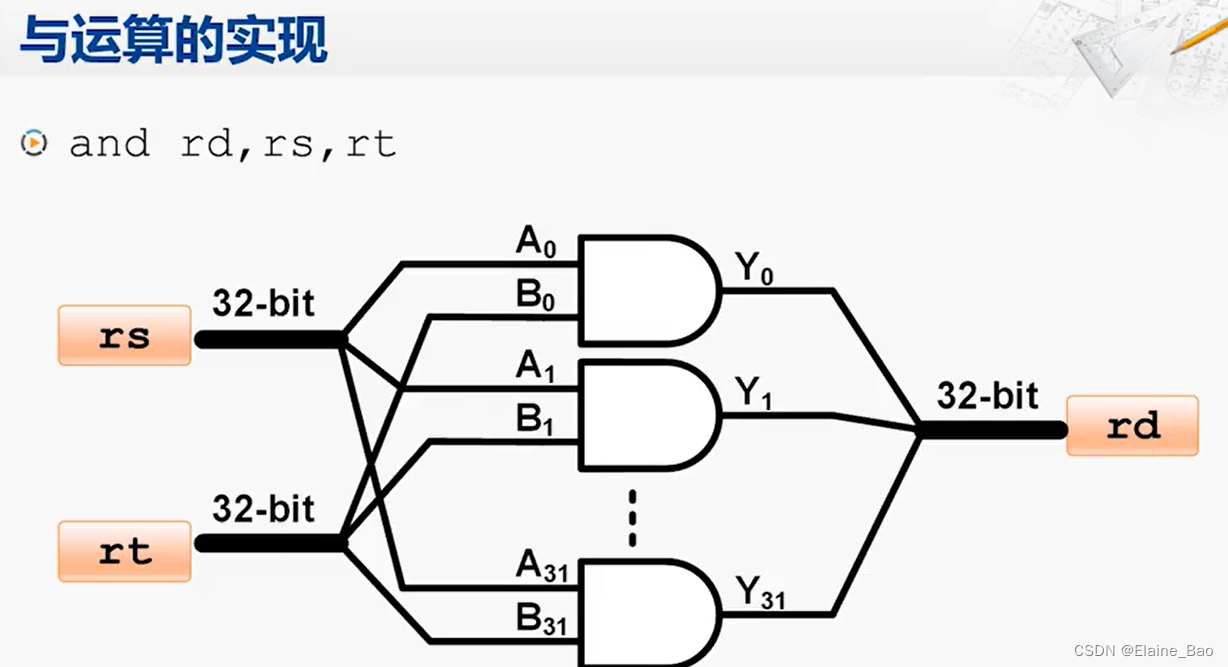
类似地，如果要完成或运算指令，则需要32个或门。

那在ALU当中，实际上是包含了多种不同的功能部件，包括刚才提到的32位的与运算，32位的或运算，以及其他的逻辑运算和算数运算。那它们是怎样合成一个整体的呢？通过一个多选器来实现，这个多选器实际上也是由若干个门组成的。

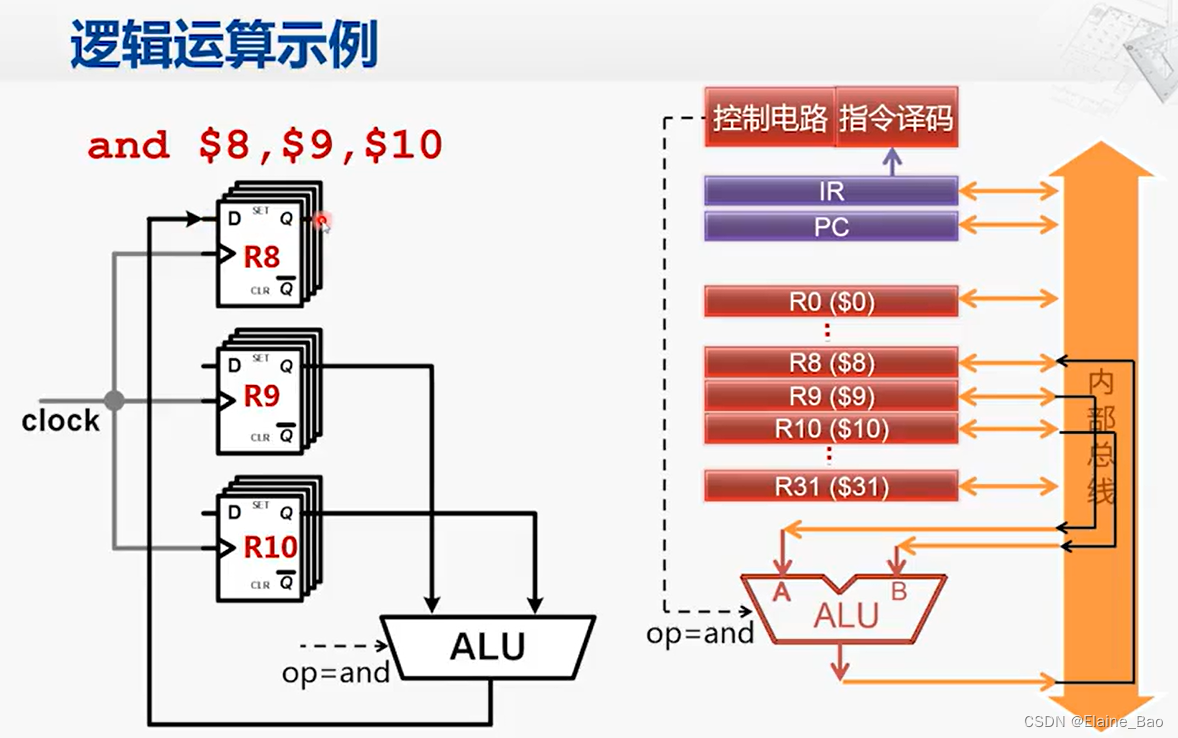
回到之前的逻辑运算的实例。如果要实现and $8,$9,$10的运算，实际上是在控制电路的控制下，将9号，10号寄存器的内容分别传送到ALU的两个输入端，根据控制电路给出的and指令进行操作，最后将结果送回到8号寄存器。

这就相当于左边这张图所显示的电路的连接。最上面是由32个D触发器组成的8号寄存器，中间是9号寄存器，下面是10号寄存器，9号和10号寄存器的Q端的输出会被连接到ALU的输入，同时ALU的功能选择信号输入了与运算所对应的编码，然后ALU的输出会被连接到8号寄存器的输入D端，所以在某一个时钟周期内，ALU会完成相关的计算，等到下一个时钟上升沿来临时，8号寄存器就会将ALU的输出存入到寄存器内部。

4. 算数运算的实现

加法和减法是两种基本的算数运算，它们在硬件上是如何实现的呢？

1. 加法运算

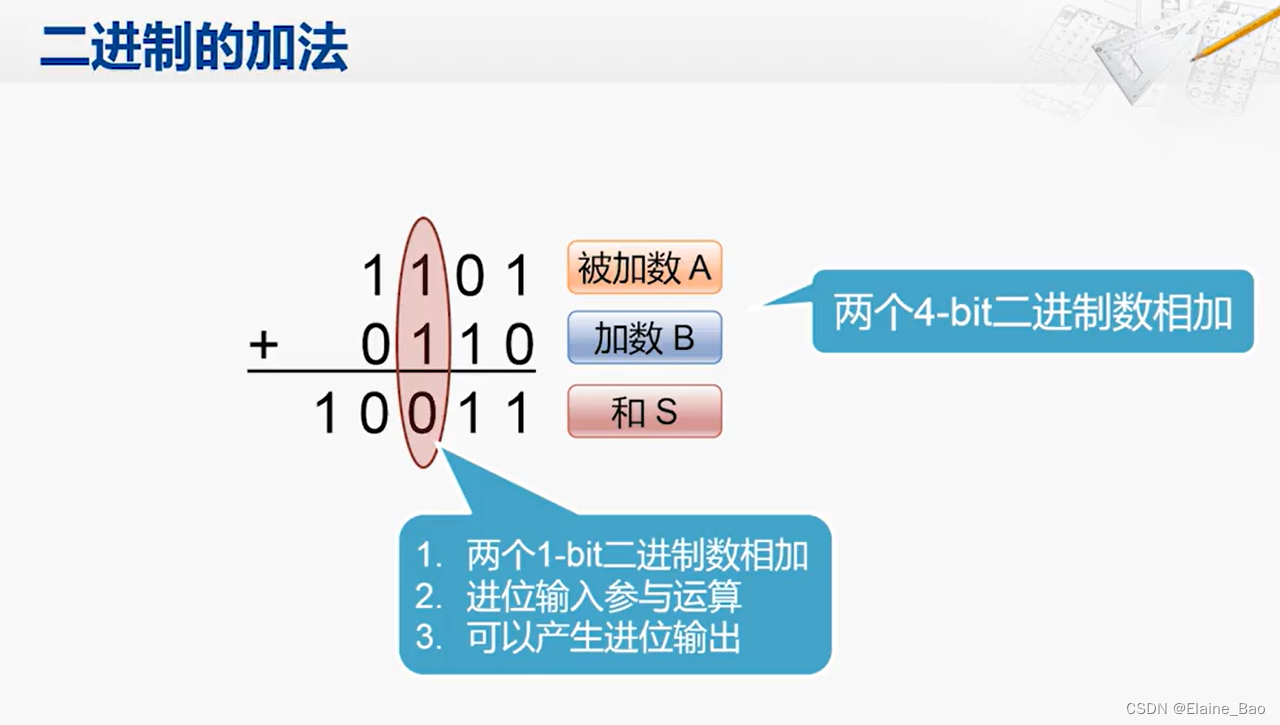
先来考虑如下两个4-bit二进制数相加的情况，对于每一位的相加来说，实际上需要做这么几项工作，1. 两个1-bit二进制数相加，2.如果低位有进位的输入的话，需要参与运算，3.最后如果产生进位，也要进行输出。

对于两个1-bit二进制数相加，可以通过半加器实现。半加器由一个异或门和一个与门组成，它有两个输入端口A,B，两个输出端口S，C(表示进位)。举例，当输入A，B分别为0，1时，异或门结果为1，与门结果为0，正好符合相加的运算。

半加器距离实现一个完整的加法运算还差一点：它不能将低位的进位输入加进来。所以为了实现这个功能，需要引入另一个半加器，构成一个全加器。

现在我们再回头看4-bit的加法，其实就是将4个全加器串联起来。

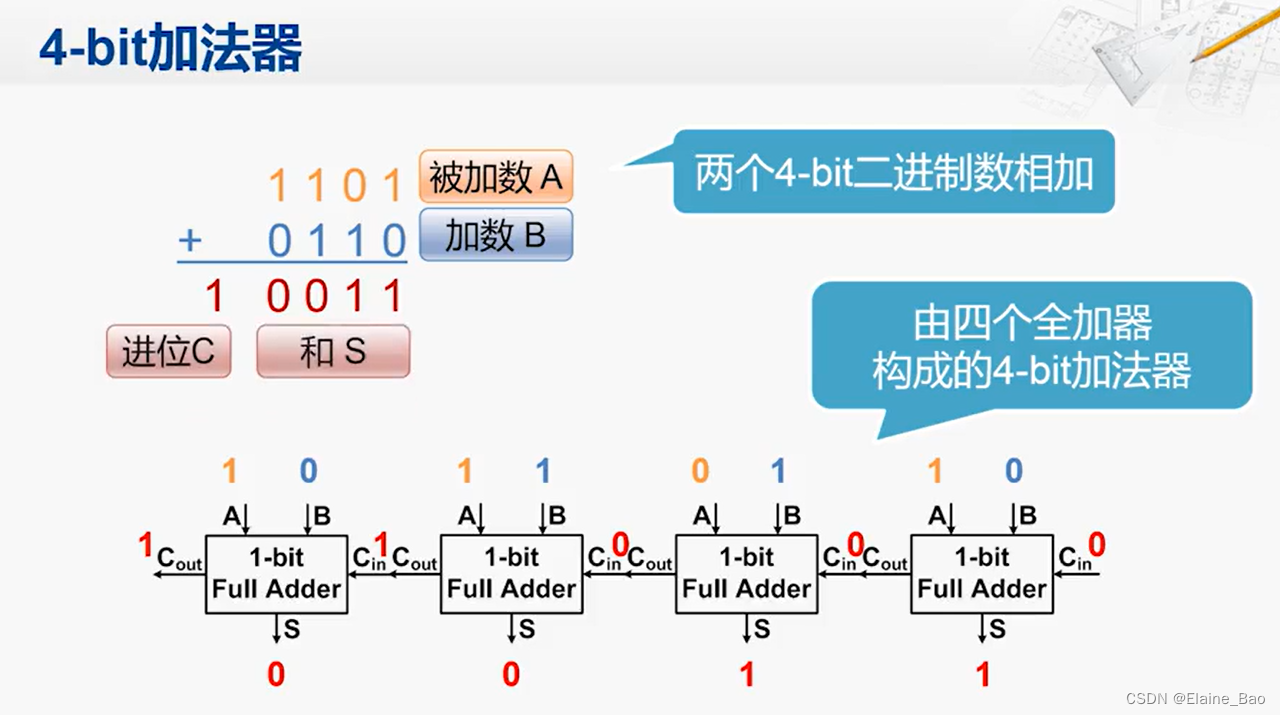
和4位加法器一样，我们可以很容易地构建出32位的加法器。这样的加法器就可以满足加法运算指令的需求。

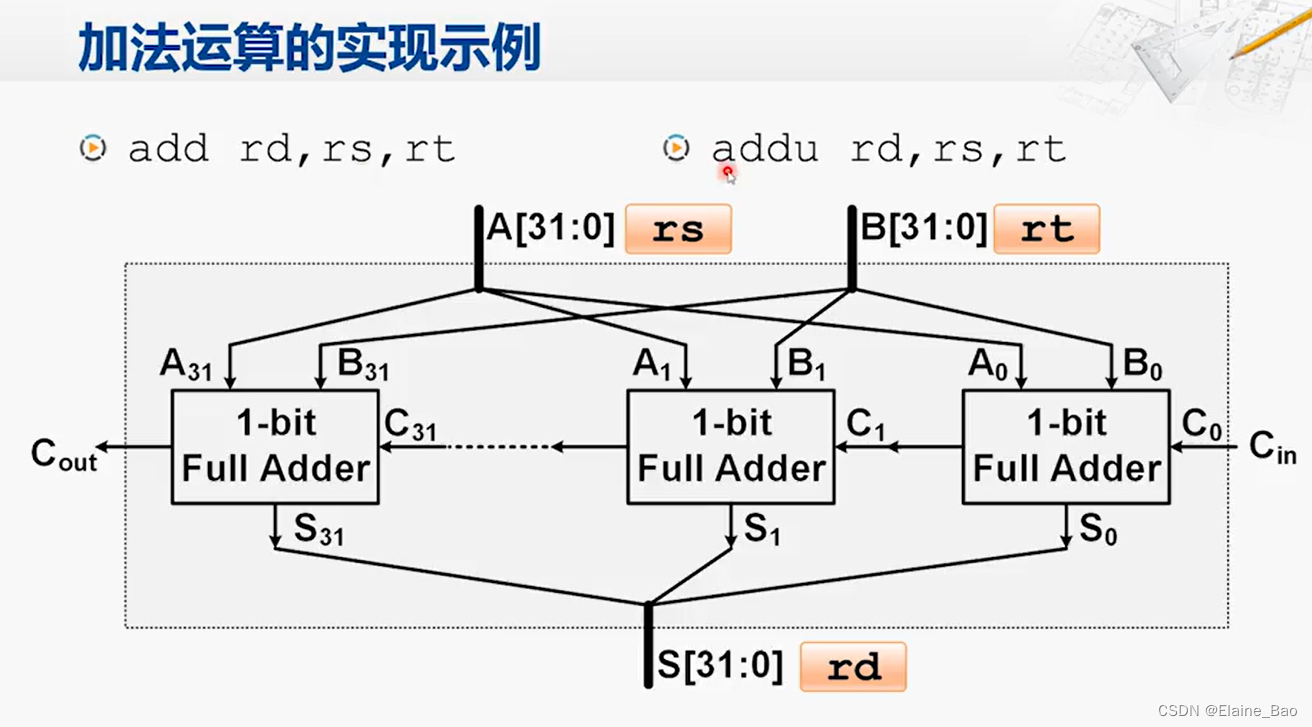
add和addu这两条指令的区别，在于对溢出的处理不同。

2. 溢出的处理

溢出（Overflow）是指运算结果超出了正常的表示范围。溢出是仅针对有符号数运算来说的。具体表现就是如果两个正数相加，结果变成了负数，或者两个负数相加，结果变成了正数，这显然是不正确的，这种情况就是由溢出造成的。

来看一个例子，0011（=3）和0101（=5）相加，如果这两个数是无符号数，那计算结果是1000（=8），是正确的，但如果是有符号数，那1000相当于-8，这就是不正确的。

这里我们还需要注意进位和溢出的差别，下面给出了两个例子，有时会出现有溢出，无进位的情况，有时也会出现有进位，无溢出的情况。因为溢出表示的是有符号数超出表示范围的情况，进位也可以看作是无符号数超出表示范围的情况。

但是进位是很好判断的，全加器本身就有进位的输出，那溢出又该如何判断呢？其实也很简单，就是当 最高位的进位输入 != 最高位的进位输出 时，就是发生了溢出。以上面的0011+0101为例，最高位的进位输入是1，而最高位的进位输出是0，此时发生了溢出。

在硬件上如何实现溢出的判断呢？可以在刚才的全加器上做一点改动。C31是最后一位的进位输入，Cout是最高位全加器的进位输出，把这两个信号连出来接一个异或门即可。

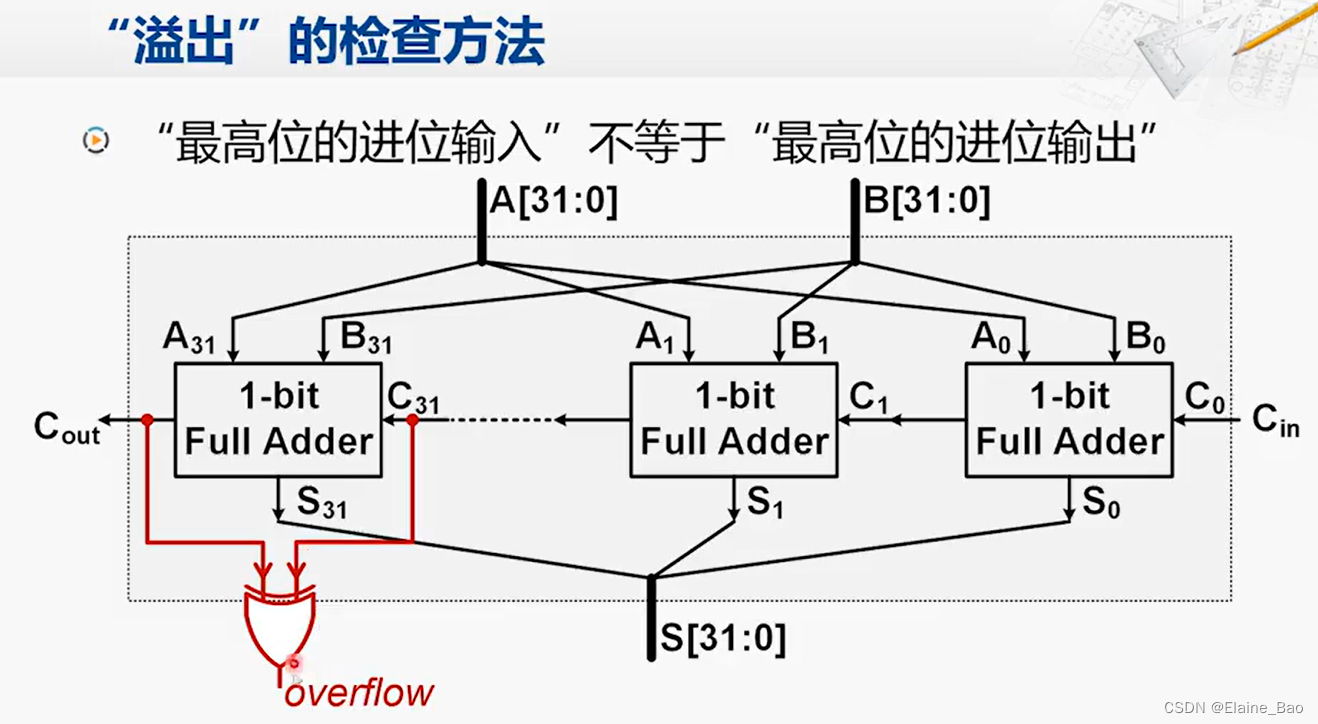
另外还需要说明的一点是，对于一个加法器的硬件实现，它并不关心这两个输入数是有符号数还是无符号数，或者说它对于有符号数和无符号数的处理是一样的。因此是不是要处理溢出，以及如何处理溢出，就不能只交给硬件来做。不同体系结构有不同的方法。

1. MIPS对溢出的处理

对于MIPS来说，它提供了两类不同的指令来分别处理。如果编程人员想将操作数看成有符号数，需要处理溢出，则需要使用add，addi指令。这样的运算在发生溢出时会产生异常，也就是说控制电路会检查加法器产生的overflow的信号，如果overflow信号有效，控制电路就会当作一个异常的情况处理。如果编程人员想将操作数堪称无符号数，不处理溢出，则需要使用addu和addiu指令。在使用这两条指令时，控制电路不会检查加法器输出的overflow信号。

所以说MIPS处理溢出的方式是提前做准备，按照是否要处理溢出采用不同的指令进行运算。

2. X86对溢出的处理

X86则采取了另一种方式。它并没有根据是否处理溢出分成两种指令，X86指令如果产生溢出，并不会直接由控制电路检查到并进行处理，而是将加法器产生的溢出信号传送到了标志寄存器的OF位。如果想对溢出进行处理，则在后续的指令中需要检查标志寄存器的OF位是否为1并进行相应的操作。

3. 减法运算

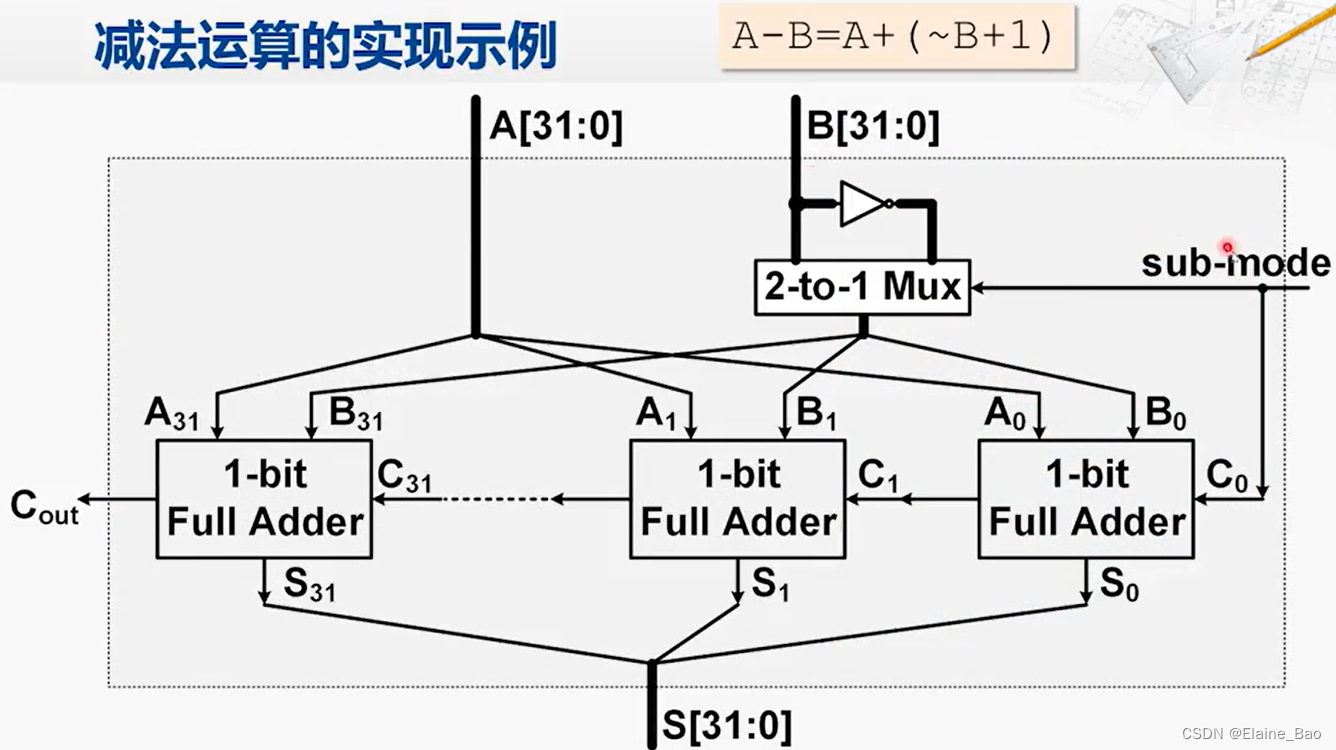
其实减法是可以很容易地转换成加法的，例如A-B=A+(-B)。但我们需要注意的是怎么把B转换成-B呢？计算机当中是用补码来保存二进制数的，把B转换成-B可不是在前面加一个负号这么简单。补码表示的二进制数的相反数有如下的转换规则：按位取反，末位加一。规则是如何来的，可以看右边的举例。

根据这个规则，我们在加法器的基础上实现减法器就容易了。在加法器的基础上，原来的输入A和B都不变，我们增加了一个新的输入，叫做sub-mode，只有1个bit，它首先控制了一个二选一的多选器，如果sub-mode=0，代表执行加法操作，那么会将多选器的左边这个通路选通。如果sub-mode=1，代表执行减法操作，这时将多选器的右边这个通路选通，此时B需要经过一个非门变成~B，同时sub-mode=1控制了C0=1，表示多加1，和减法的计算公式相符。

这样我们通过这个改动，这个功能部件又能实现加法，又能实现减法。

4. 加法器的优化

ALU提供的加法和减法，究其本质都是由加法器来实现的。我们现在学习的加法器，是由一个一个的全加器串联而成，它在性能上存在着很大的问题。以4-bit加法器为例，当把所有输入都准备好时，其实只有最右边的全加器可以开始工作，等它计算完了产生新的进位，第二个全加器才能开始工作。这样进位输出像波浪一样从低位向高位传递的加法器叫做行波进位加法器（Ripple-Carry Adder, RCA）。这种加法器的优点是电路布局简单，设计方便。它的缺点也很明显，就是高位的运算必须等待低位的运算完成，延迟时间长。

我们来分析一下行波进位加法器的延迟情况。延迟最长的路径（也被称为关键路径）的延迟时间是（2n+1）T。也就是说对于4-bit的加法器，延迟时间是9T，对于32-bit的加法器，延迟时间是65T。

这个时间，参考28nm的制造工艺，1.3GHz的主频表示时钟周期是0.66ns，这就是最近的两个时钟上升沿之间的时间长度。因为加法器的输入是来自寄存器，而且加法器的输出，包括运算的核，进位的输出，都是要传递到寄存器保存起来的，所以说这些信号从前一级的寄存器经过加法器的所有逻辑一直到下一级寄存器的输入，不能超过0.66ns。但实际情况是，对于32-bit RCA来说，延迟时间大约为1.3ns，远远超过了0.66ns。采用这样的加法器，它的主时钟频率最多也只能达到769MHz。所以说这样的加法器与现实中使用的加法器，性能差距是非常大的。那我们应该如何进行优化呢？

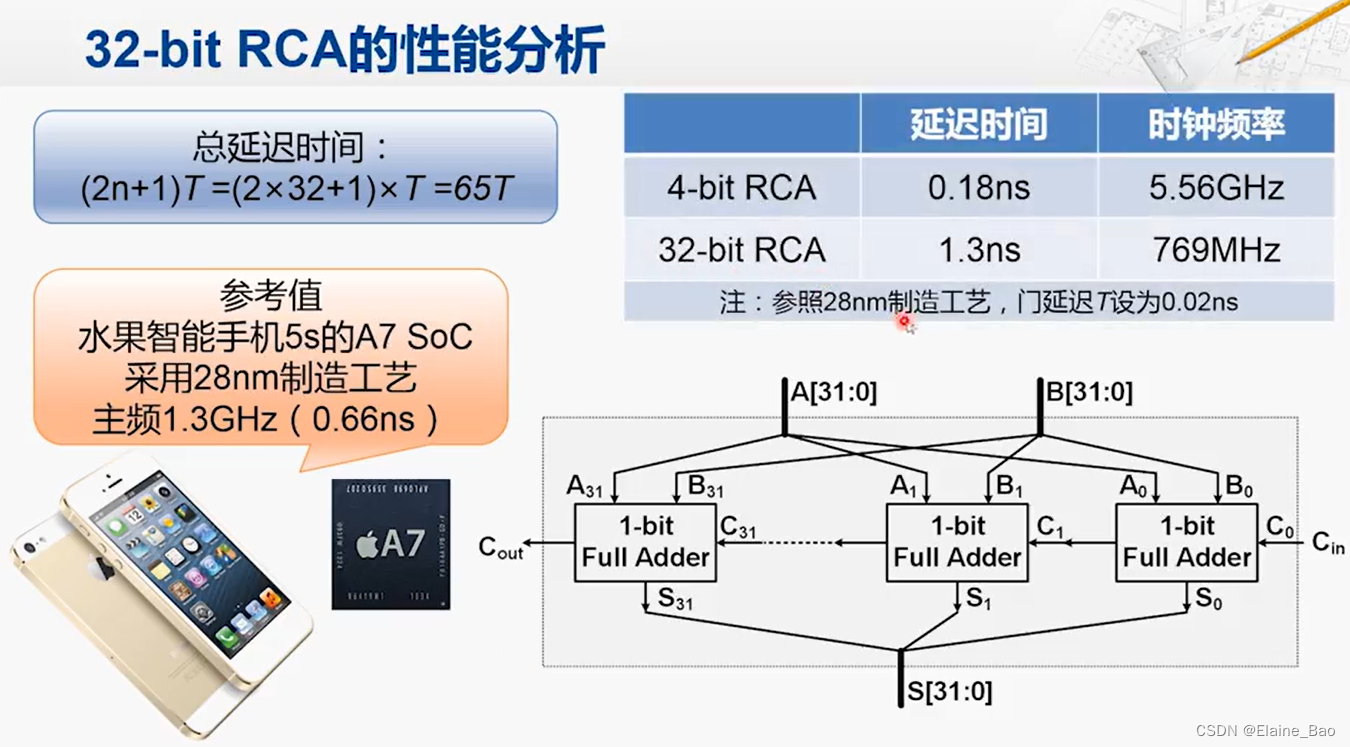
分析行波进位加法器的问题所在，影响性能的主要问题在于高位的运算必须等待低位的进位输出信号。那么优化思路就是，能否提前计算进位输出信号？

我们对进位输出信号进行分析。对于每一个全加器，它的进位输出信号记为Ci+1，它能通过3个输入（Ai,Bi,Ci）计算得到。通过换算，我们设置两个新的变量Gi和Pi，这两个变量是由Ai和Bi产生的，他们都是在运算之初就能确定了的信号。

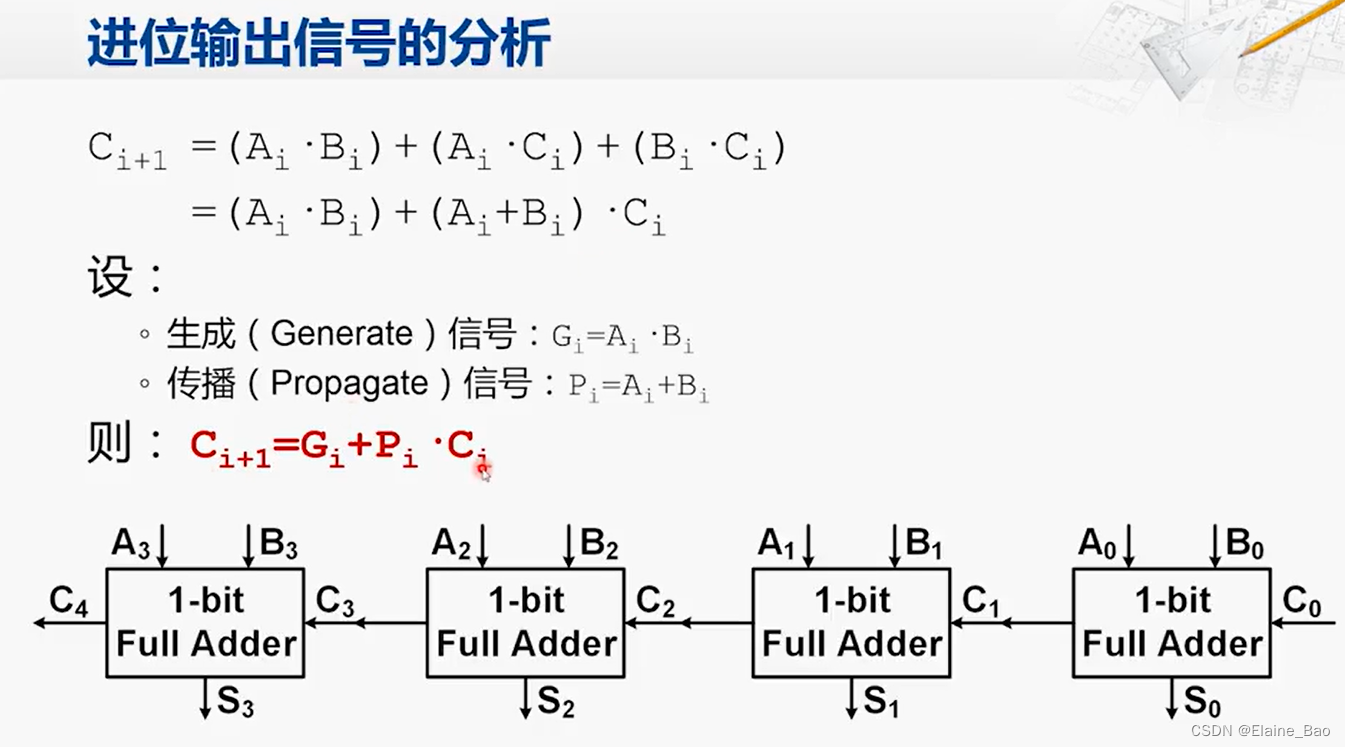
通过代入计算，C1,C2,C3,C4都能够通过Gi,Pi和C0计算得到，这些都是在运算之初就能确定了的信号，因此我们就有了提前计算进位输出信号的方法。用这样的方法实现的加法器叫做超前进位加法器（Carry-Lookahead Adder, CLA）。

那它在硬件上是如何实现的呢？如下图，可以看到计算Ci+1的延迟时间固定为3级门延迟，与加法器的位数无关。然后最后一级的全加器还要计算S位的输出，因此再多1级门延迟，总延迟时间为4T。

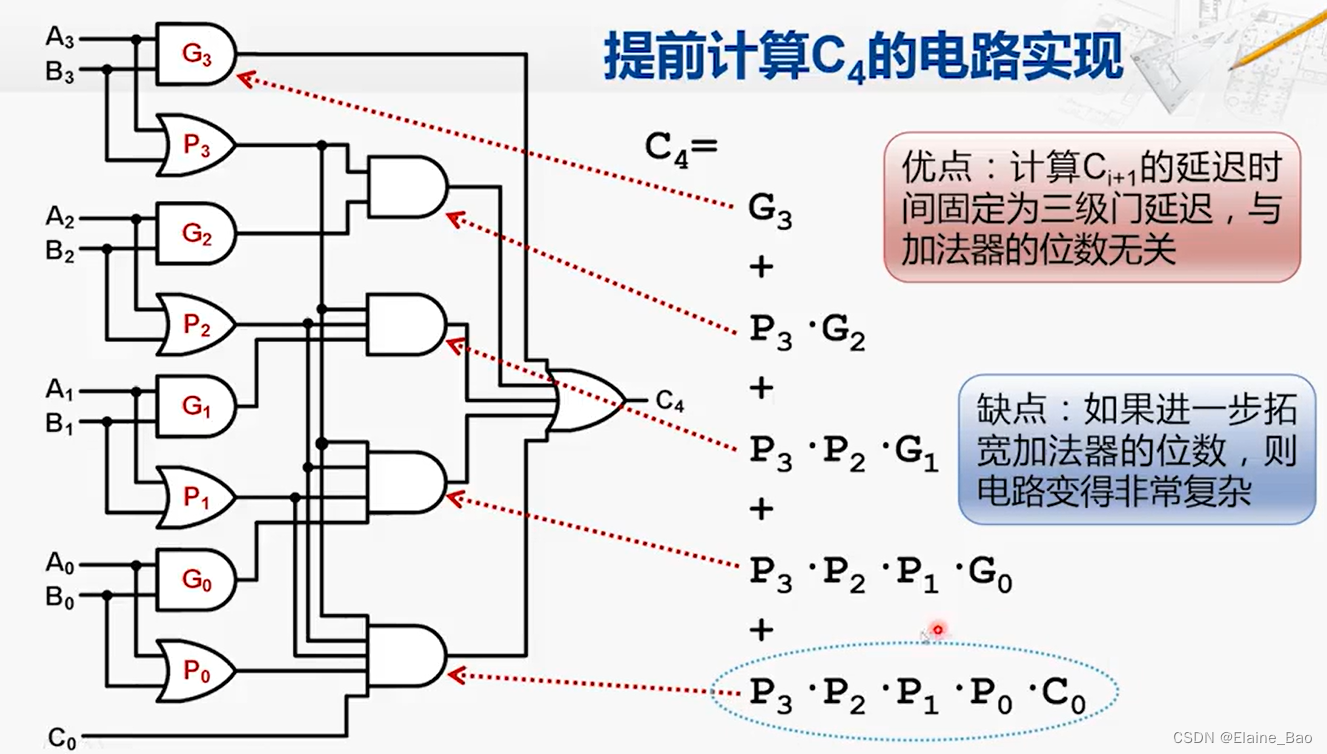
我们再考虑32-bit加法器，如果采用行波进位加法器，总延迟时间为65T，如果采用超前进位加法器，理想的总延迟时间为4T，但是实际上电路过于复杂，难以实现。所以通常的实现方法，是采用多个小规模的超前进位加法器拼接而成，例如用4个8-bit的超前进位加法器用行波进位的方式连接起来，从而构成一个32-bit的加法器。这样的实现下，4级CLA的延迟时间为0.26ns（0.02*3级门延迟得到C4*3级CLA+0.02*4级门延迟得到S*最后1级CLA=0.26ns），这样就可以运行在3.84GHz的时钟频率下，那么它就不会成为我们整个复杂的CPU设计的关键路径了。