探索树堆Treap和红黑树的优势和劣势

一、背景知识
二、树堆（Treap）的介绍
三、红黑树（RB-Tree）的介绍
四、树堆（Treap）与红黑树（RB-Tree）的比较
总结

博主简介

💡一个热爱分享高性能服务器后台开发知识的博主，目标是通过理论与代码实践的结合，让世界上看似难以掌握的技术变得易于理解与掌握。技能涵盖了多个领域，包括C/C++、Linux、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、协程、DPDK等。
👉
🎖️ CSDN实力新星、CSDN博客专家、华为云云享专家、阿里云专家博主
👉

一、背景知识

树堆（Treap）和红黑树（RB-Tree）都是常见的自平衡二叉搜索树（self-balancing binary search tree）数据结构。
在这里插入图片描述

树堆是一种随机化平衡二叉搜索树，结合了二叉堆和二叉搜索树的特性。树堆的每个节点包含一个键值和一个随机优先级值。树堆的特点是通过维护键值的二叉搜索树性质和优先级的堆性质来保持平衡。通过保持这两个性质，树堆可以在插入和删除节点时自动进行平衡操作。树堆的优势在于它相对简单的实现和高效的查找操作。
在这里插入图片描述

红黑树是一种严格平衡的自平衡二叉搜索树。每个节点都具有一个额外的标记，称为颜色，可以是红色或黑色。红黑树通过遵循一组特定的规则来保持平衡，如保持从根节点到叶节点的任何路径上的黑色节点数量相同。通过这些规则，红黑树可以在插入和删除节点时自动进行平衡操作。红黑树的优势在于它提供严格的平衡性能保证，并且具有高效的查找、插入和删除操作。
在这里插入图片描述
区别：

树堆通过随机优先级来维持平衡，而红黑树则通过颜色标记和旋转操作来维持平衡。
树堆在实现和维护方面相对简单，而红黑树提供了严格的平衡保证。

探索树堆（Treap）和红黑树（RB-Tree）的优势和劣势的目的在于深入了解这两种常见的自平衡二叉搜索树数据结构，可以帮助我们优化和改进现有的数据结构，或者在需要特定性能要求的场景中提出新的数据结构设计。

二、树堆（Treap）的介绍

树堆（Treap）是一种组合了二叉堆和二叉搜索树特性的随机化平衡二叉树。它的基本特性和原理：

键值特性：树堆的每个节点包含一个键值和一个随机的优先级值。键值用于节点的比较和排序，优先级值用于平衡树的结构。
二叉搜索树性质：树堆维护了二叉搜索树的性质，即对于任意节点，它的左子树中的所有节点的键值小于该节点的键值，右子树中的所有节点的键值大于该节点的键值。
堆性质：树堆也维护了堆的性质，即对于任意节点，它的优先级值大于其子节点的优先级值。
随机化平衡：树堆通过随机生成节点的优先级值来实现平衡。节点的优先级值和键值无关，它的随机性保证了树的平衡性质。
插入操作：当插入一个新节点时，树堆首先按照二叉搜索树性质找到插入的位置，然后根据节点的优先级值，通过旋转操作保持堆性质和搜索树性质。
删除操作：删除一个节点时，树堆首先根据二叉搜索树性质找到要删除的节点，然后通过旋转操作将其删除，并保持堆性质和搜索树性质。

因此，树堆被广泛应用于各种需要动态操作集合的场景，如数据库索引、动态统计和优先级队列等。

树堆的优点：

随机化特性和平衡性。树堆通过随机化的方式维护平衡，在大多数情况下可以保持较好的性能，而不需要过多的平衡调整操作。
相对简单的实现，减少了开发和维护的复杂性。
提供高效的查找、插入和删除操作。树堆通过旋转操作和优先级调整，在插入和删除节点时能够自动进行平衡操作。相对于其他平衡树结构，树堆的插入和删除操作具有较低的时间复杂度。

简单的树堆（Treap）的C语言代码实现，以便更好地理解其工作原理：

#include <stdio.h>
#include <stdlib.h>// 定义树堆节点结构体
typedef struct treap_node {int key;int priority;struct treap_node* left;struct treap_node* right;
} TreapNode;// 初始化树堆节点
TreapNode* createNode(int key) {TreapNode* node = (TreapNode*)malloc(sizeof(TreapNode));node->key = key;node->priority = rand() % 100;  // 随机生成优先级值node->left = NULL;node->right = NULL;return node;
}// 左旋
void leftRotate(TreapNode** node) {TreapNode* newRoot = (*node)->right;(*node)->right = newRoot->left;newRoot->left = (*node);*node = newRoot;
}// 右旋
void rightRotate(TreapNode** node) {TreapNode* newRoot = (*node)->left;(*node)->left = newRoot->right;newRoot->right = (*node);*node = newRoot;
}// 树堆插入操作
void insert(TreapNode** root, int key) {if ((*root) == NULL) {*root = createNode(key);return;}if (key < (*root)->key) {insert(&((*root)->left), key);if ((*root)->left && (*root)->left->priority > (*root)->priority) {rightRotate(root);}} else {insert(&((*root)->right), key);if ((*root)->right && (*root)->right->priority > (*root)->priority) {leftRotate(root);}}
}// 前序遍历树堆
void preOrderTraversal(TreapNode* root) {if (root == NULL) {return;}printf("Key: %d, Priority: %d
", root->key, root->priority);preOrderTraversal(root->left);preOrderTraversal(root->right);
}int main() {TreapNode* root = NULL;// 插入节点insert(&root, 8);insert(&root, 5);insert(&root, 12);insert(&root, 3);insert(&root, 10);// 前序遍历输出树堆preOrderTraversal(root);return 0;
}

三、红黑树（RB-Tree）的介绍

红黑树本质上是一个二叉树。
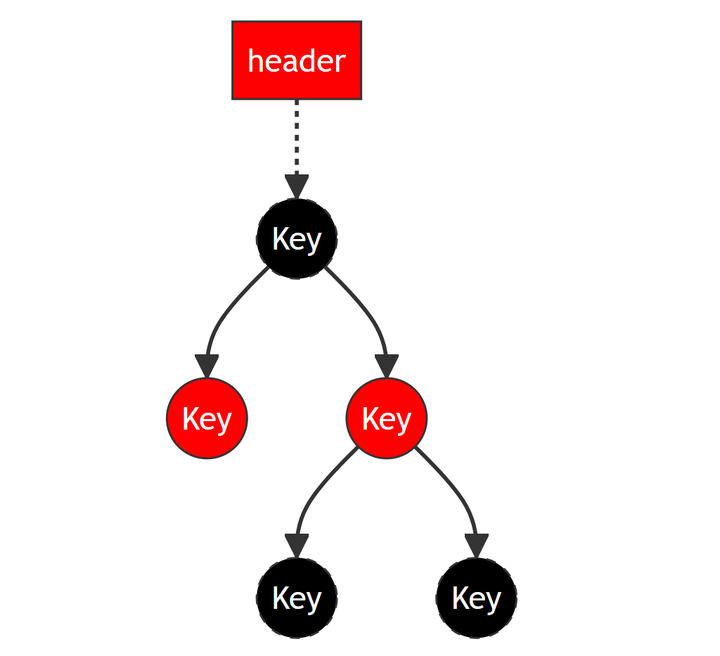
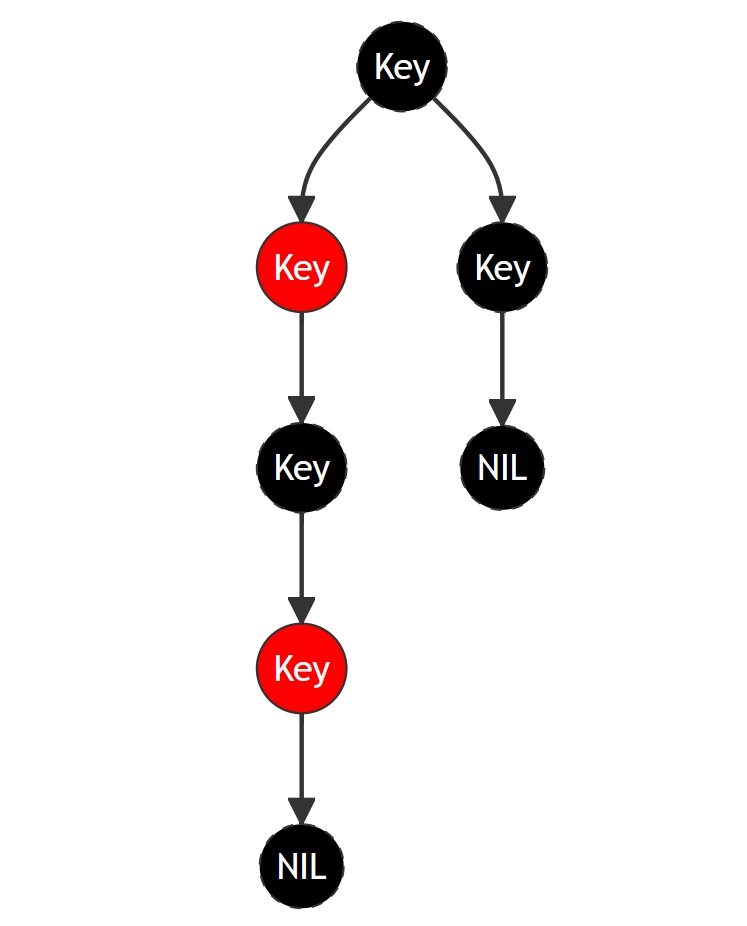
在这里插入图片描述

红黑树在二叉树的基础上具备如下的性质：

每个结点是红的或者黑的。
根结点是黑的。
每个叶子结点是黑的。
如果一个结点是红的，则它的两个儿子都是黑的。
对每个结点，从该结点到其子孙结点的所有路径上的包含相同数目的黑结点。

满足以上性质的二叉树就是红黑树。其中第五条性质就决定了红黑树的平衡，它不像AVL树那样严格要求两边子树的高度差是1，而是要求黑色节点的高度一致即可。

从第四条和第五条的性质中，我们可以总结出一个数学结论：红黑树的根节点到叶子节点的最短路径与红黑树的根节点到叶子节点的最长路径之比是 $:（2\times N-1）$ 。
在这里插入图片描述
红黑树的优点：

严格的平衡性能保证。红黑树通过遵循一组严格的规则来保持平衡，如保持从根节点到叶节点的任何路径上的黑色节点数量相同。这种平衡性能保证了红黑树的最坏情况时间复杂度为O(logN)。
高效的查找、插入和删除操作。由于红黑树是二叉搜索树，通过颜色标记和旋转操作来维持平衡，操作具有较低的时间复杂度。
作为一种高效的自平衡树结构，被用于实现C++ STL的map、set等数据结构，以及数据库索引、编译器实现、网络路由算法等领域。

四、树堆（Treap）与红黑树（RB-Tree）的比较

红黑树和树堆在查找、插入和删除操作上的平均性能是相似的，都是O(log n)。这是因为它们都是自平衡的二叉搜索树，通过调整树的结构来维护平衡性，以确保这些操作的时间复杂度保持在对数级别。
树堆的空间复杂度通常较低，适用于需要高效的优先队列操作的场景。而红黑树的空间复杂度较高，但由于其自平衡性质，它在搜索、插入和删除等操作上具有良好的性能。
树堆的实现复杂度相对较低，特别是在插入和删除操作上。红黑树相对复杂一些，具有更好的平衡性，可以保证树的高度较小，从而在查找操作上表现更好。
如果需要频繁的插入和删除操作，并且对查找操作的性能要求不是特别高，那么树堆可能是一个更好的选择，因为它们在动态插入和删除方面更有效率。如果对查找操作的性能要求较高，希望确保树的平衡性，或者需要一种稳定的数据结构，那么红黑树可能更适合，因为它们在保持平衡和查找操作上具有更好的性能保证。