-
查看 myslq 是否安装:
rpm -qa|grep mysql- 如果已经安装,可执行命令来删除软件包:
rpm -e --nodeps 包名
- 如果已经安装,可执行命令来删除软件包:
- 下载 repo 源:
http://dev.mysql.com/get/mysql80-community-release-el7-7.noarch.rpm - 执行命令安装 rpm 源(根据下载的 rpm 源进行选择)
#CentOS7 安装mysql8 rpm -ivh mysql80-community-release-el7-7.noarch.rpm
- 查看 mysql yum 仓库中 mysql 版本,使用如下命令
yum repolist all | grep mysql
- 可以看到 MySQL 5.5 5.6 5.7 为禁用状态,而 Mysql 8.0 为启用状态
- 修改相对应的版本为启用状态最新版本为禁用状态(自行选择)
yum-config-manager --disable mysql80-community yum-config-manager --enable mysql57-community
- 查看 mysql yum 仓库中 mysql 版本,使用如下命令
- 安装 MySQL 服务:
#安装mysql服务 yum install mysql-community-server #查看mysql版本 mysql -V
- 启动 MySQL:
#查看mysql运行状态 systemctl status mysqld.service #启动mysql systemctl start mysqld #停止mysql systemctl stop mysqld #重启mysql systemctl restart mysqld- 开启 mysql 开机自启动:
#开启mysql开机自启动 systemctl enable mysqld #关闭mysql开机自启动 systemctl disable mysqld
- 开启 mysql 开机自启动:
- 设置 mysql 密码:
- 获取临时密码
//获取MySQL临时密码 grep 'temporary password' /var/log/mysqld.log
- 登录 mysql:密码是上面获取的临时密码
//登录mysql mysql -uroot -p
- 用临时密码登陆后,设置 mysql 永久密码:
show variables like 'validate_password.%'; //根据下图中的密码策略设置mysql数据库密码(你不设置密码就无法进行其它操作) alter user 'root'@'localhost' identified by 'Zjx123456#';
- 注意:你的密码不符合密码策略的话是无法设置成功的,mysql8 默认密码策略如下图(最少 8 位,至少包含一个数字,至少包含一个特殊字符)

- 获取临时密码
- 修改密码策略:
- 只能临时修改密码策略,重启 mysql 后自动恢复默认密码策略,想要永久修改 mysql 配置文件,一般来说临时修改密码策略就够了
//设置密码长度 set global validate_password.length = 6; //设置密码风险等级(等级越高要求密码越复杂),分为0、1、2级 set global validate_password.policy = 0;//查询密码策略 show variables like 'validate_password.%';//设置mysql数据库密码 (这里是密码) alter user 'root'@'localhost' identified by 'Zjx123456#';
- 只能临时修改密码策略,重启 mysql 后自动恢复默认密码策略,想要永久修改 mysql 配置文件,一般来说临时修改密码策略就够了
- 许外部访问 mysql 数据库:
//创建用户(远程连接用的账号) (远程连接用的密码) create user 'root'@'%' identified by 'mypassword'; //mysql8.0版本 //create user 'root'@'%' identified with mysql_native_password by 'Zjx123456#';//分配权限,运行远程连接(允许root账号远程连接) grant all privileges on *.* to 'root'@'%' with grant option;//刷新权限 flush privileges;
- 远程链接数据库,如果远程连接不上,考虑防火墙是否开放了 mysql 端口 (3306) 和服务器上的 MySQL 端口(3306)
- 在使用 Navicat for mysql 链接 mysql 8.0时会报如下错误:
Authentication plugin 'caching_sha2_password' cannot be loaded: - mysql 8.0 引入了新特性 caching_sha2_password,这种密码加密方式客户端不支持,客户端支持的是 mysql_native_password 这种加密方式
- 我们可以查看 mysql 数据库中 user 表的 plugin 字段
use mysql; select host,user,plugin from user;
- 可以使用命令将他修改成 mysql_native_password 加密方式:
update user set plugin='mysql_native_password' where user='root'; //或者创建user时直接指定加密模式 create user 'root'@'%' identified with mysql_native_password by 'Zjx123456#';
Linux环境下的Java项目部署技巧:安装 Mysql
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/11716.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
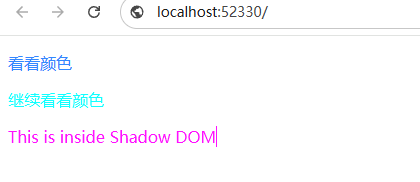
Shadow DOM举例
这东西具有隔离效果,对于一些插件需要append一些div倒是不错的选择 <!DOCTYPE html>
<html lang"zh-CN">
<head>
<meta charset"utf-8">
<title>演示例子</title>
</head>
<body>
<style&g…
万字长文深入浅出负载均衡器
前言
本篇博客主要分享Load Balancing(负载均衡),将从以下方面循序渐进地全面展开阐述:
介绍什么是负载均衡介绍常见的负载均衡算法
负载均衡简介
初识负载均衡
负载均衡是系统设计中的一个关键组成部分,它有助于…
ChatGPT-4o和ChatGPT-4o mini的差异点
在人工智能领域,OpenAI再次引领创新潮流,近日正式发布了其最新模型——ChatGPT-4o及其经济实惠的小型版本ChatGPT-4o Mini。这两款模型虽同属于ChatGPT系列,但在性能、应用场景及成本上展现出显著的差异。本文将通过图文并茂的方式࿰…
双指针算法思想——OJ例题扩展算法解析思路
大家好!上一期我发布了关于双指针的OJ平台上的典型例题思路解析,基于上一期的内容,我们这一期从其中内容扩展出来相似例题进行剖析和运用,一起来试一下吧! 目录
一、 基于移动零的举一反三
题一:27. 移除…
WSL2中安装的ubuntu开启与关闭探讨
1. PC开机后,查询wsl状态
在cmd或者powersell中输入
wsl -l -vNAME STATE VERSION
* Ubuntu Stopped 22. 从windows访问WSL2
wsl -l -vNAME STATE VERSION
* Ubuntu Stopped 23. 在ubuntu中打开一个工作区后…
git笔记-简单入门
git笔记 git是一个分布式版本控制系统,它的优点有哪些呢?分为以下几个部分 与集中式的版本控制系统比起来,不用担心单点故障问题,只需要互相同步一下进度即可。支持离线编辑,每一个人都有一个完整的版本库。跨平台支持…
Chapter2 Amplifiers, Source followers Cascodes
Chapter2 Amplifiers, Source followers & Cascodes
MOS单管根据输入输出, 可分为CS放大器, source follower和cascode 三种结构.
Single-transistor amplifiers
这一章学习模拟电路基本单元-单管放大器
单管运放由Common-Source加上DC电流源组成. Avgm*Rds, gm和rds和…
LabVIEW透镜多参数自动检测系统
在现代制造业中,提升产品质量检测的自动化水平是提高生产效率和准确性的关键。本文介绍了一个基于LabVIEW的透镜多参数自动检测系统,该系统能够在单一工位上完成透镜的多项质量参数检测,并实现透镜的自动搬运与分选,极大地提升了检…
K8S集群部署--亲测好用
最近在自学K8S,花了三天最后终于成功部署一套K8S Cluster集群(masternode1node2)
在这里先分享一下具体的步骤,后续再更新其他的内容:例如部署期间遇到的问题及其解决办法。
部署步骤是英文写的,最近想练…
PHP实现混合加密方式,提高加密的安全性(代码解密)
代码1:
<?php
// 需要加密的内容
$plaintext 授权服务器拒绝连接;// 1. AES加密部分
$aesKey openssl_random_pseudo_bytes(32); // 生成256位AES密钥
$iv openssl_random_pseudo_bytes(16); // 生成128位IV// AES加密(CBC模式)…
Linux - 进程间通信(3)
目录
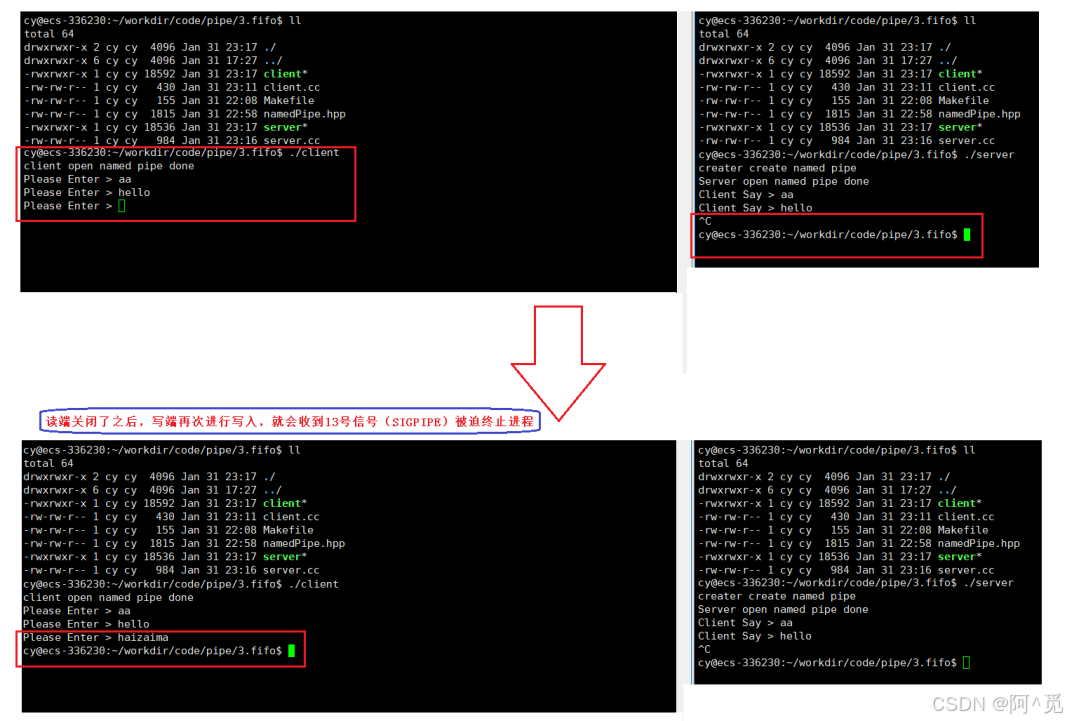
3、解决遗留BUG -- 边关闭信道边回收进程
1)解决方案
2)两种方法相比较
4、命名管道
1)理解命名管道
2)创建命名管道
a. 命令行指令
b. 系统调用方法
3)代码实现命名管道
构建类进行封装命名管道&#…
C语言 --- 分支
C语言 --- 分支 语句分支语句含义if...else语句单分支if语句语法形式 双分支 if-else 语句语法形式 悬空else含义问题描述 多分支 if-else 语句语法形式 switch...case语句含义语法形式 总结 💻作者简介:曾与你一样迷茫,现以经验助你入门 C 语…
SSRF 漏洞利用 Redis 实战全解析:原理、攻击与防范
目录
前言
SSRF 漏洞深度剖析
Redis:强大的内存数据库
Redis 产生漏洞的原因
SSRF 漏洞利用 Redis 实战步骤
准备环境
下载安装 Redis
配置漏洞环境
启动 Redis
攻击机远程连接 Redis
利用 Redis 写 Webshell
防范措施
前言
在网络安全领域࿰…
Spring Boot - 数据库集成06 - 集成ElasticSearch
Spring boot 集成 ElasticSearch 文章目录 Spring boot 集成 ElasticSearch一:前置工作1:项目搭建和依赖导入2:客户端连接相关构建3:实体类相关注解配置说明 二:客户端client相关操作说明1:检索流程1.1&…
深度学习之“线性代数”
线性代数在深度学习中是解决多维数学对象计算问题的核心工具。这些数学对象包括标量、向量、矩阵和张量,借助它们可以高效地对数据进行操作和建模。以下将详细介绍这些数学对象及其在深度学习中的典型用途。
数学对象概述
标量
标量是最简单的数学对象࿰…
使用PyQt5绘制带有刻度的温度计控件
前言:进入学习Python开发上位机界面的第二阶段,学习如何开发自定义控件,从常用的控件入手学习,本期主要学习如何使用PyQt5绘制带有刻度的温度计控件。
1. 先找到一篇参考文章
参考文章:Qt编写自定义控件5-柱状温度计…
问deepseek,如何看待ai降低学习成本而导致软件开发岗位需求降低,和工资下降。 软件从业人员何去何从?
它给我的回答是这样的: 思考逻辑
嗯,用户问的是AI如何降低学习成本,进而导致软件开发岗位需求减少和工资下降,以及软件从业人员该怎么办。这个问题挺复杂的,我得先理清楚各个部分。首先,AI确实在改变很多行…
推荐文章
- ffmpeg -formats
- MVC(Model-View-Controller)framework using Python ,Tkinter and SQLite
- 堆排序
- (动态规划基础 打家劫舍)leetcode 198
- (学习总结21)C++11 异常与智能指针
- .NET Framework
- [操作系统] 基础 IO:理解“文件”与 C 接口
- [今年毕业设计]最新最全最有创意的基于云计算的计算机专业毕设选题精选推荐汇总建议收藏!!
- “深入浅出”系列之C++:(5)STL标准模板库详解
- 《 C++ 点滴漫谈: 二十五 》空指针,隐秘而危险的杀手:程序崩溃的真凶就在你眼前!
- 《机器学习》——贝叶斯算法
- 《使用人工智能心脏磁共振成像筛查和诊断心血管疾病》论文精读