超图嵌入论文阅读1:对偶机制非均匀超网络嵌入
原文:Nonuniform Hyper-Network Embedding with Dual Mechanism ——TOIS(一区 CCF-A)
背景
超边:每条边可以连接不确定数量的顶点
我们关注超网络的两个属性:非均匀和对偶属性。
贡献:
- 提出了一种称为 Hyper2vec 的灵活模型,通过在 Skip-gram 框架下对超网络应用有偏二阶随机游走策略来学习超网络的嵌入;
- 通过对偶超网络来构建进一步的模型来组合超边的特征,称为NHNE,基于一维卷积神经网络。训练了一个元组相似函数来建模非均匀关系。
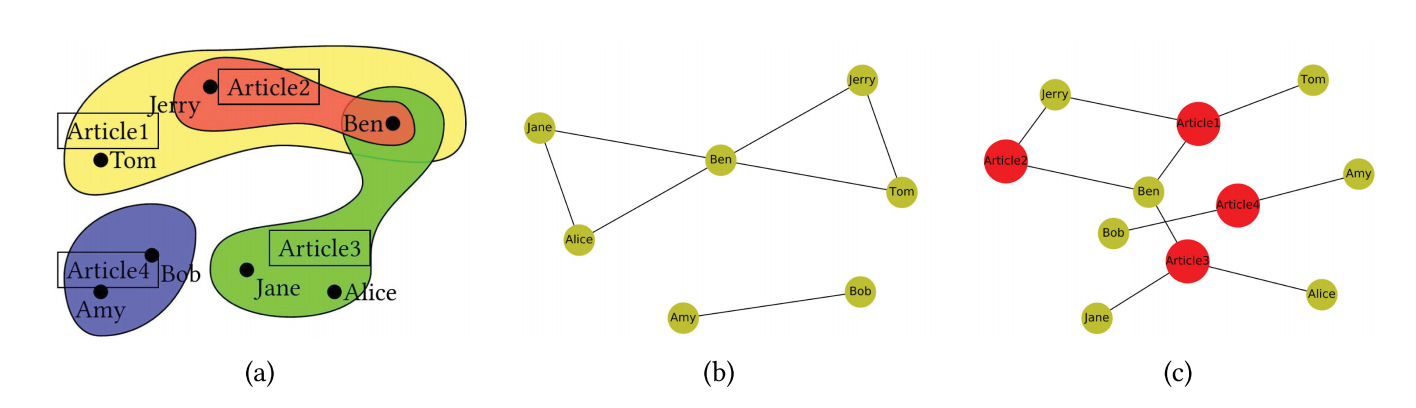
现状:
-
很少有网络嵌入方法可以直接应用于超网络——无法直接推广。
-
传统方法是将它们转换为正常网络:团扩展、星扩展——显式或隐式导致原始超网络的信息丢失
如:团扩展将所有超边平均转换为正常边,这改变了顶点之间的关系,丢失了超边的信息。因为元组关系所暗示的所有可能的边都被平等对待,并且不再存在元组关系
-
到2020年为止,只有几种超网络嵌入方法被提出,主要是为具有特定属性(如均匀性和不可分解性)的超网络设计的,因此不能提高在广泛的超网络上的性能。——当前其他方法泛化能力差
本工作对超网络的独特观察:
- 非均匀:超网络中的超边通常是不均匀的——需要具有可变长度输入的函数来预测包含不同数量的顶点的超边
- 对偶性:超图的对偶网络具有显着的含义——可以用来捕获超边的高阶邻近度和结构属性等(原始超网络建模中可能丢失)
评估实验:链接预测、顶点分类
相关工作
传统图嵌入
-
经典的网络嵌入方法:LLE、拉普拉斯特征映射、IsoMap
-
随机游走嵌入方法(基于Skip-gram思想):DeepWalk(一阶游走)、Node2vec(二阶游走)
-
大规模网络嵌入方法:LINE(保留一阶和二阶邻近性)、SDNE、SDAE和SiNE(深度网络学习顶点嵌入)
-
邻域聚合编码器:依赖于顶点的特征和属性、很难应用于无监督任务
超图嵌入:
-
基于谱聚类技术:谱聚类假设图割对分类有用——泛化能力差。
-
均匀超图嵌入:异构超图嵌入(HHE)、超图嵌入(HGE)、深度超网络嵌入(DHNE)和异构超网络嵌入(HHNE)
- HHE通过求解与超网络拉普拉斯矩阵相关的特征向量问题来学习嵌入,但它既费时又耗空间。
- HGE通过将多路关系合并到与几何均值和算术平均值相关的优化问题中来学习嵌入,但它不灵活,无法很好地捕获非均匀超网络的特征。
- DHNE是一种基于神经网络的超网络嵌入模型,但它仅适用于具有高不可分解超边的统一异构超网络。
- HHNE利用图卷积网络来学习顶点的嵌入,但它依赖于顶点的特征,在无监督环境下很难应用于分类任务。
-
二分(星形)扩展嵌入:多用于推荐——二分网络嵌入 (BiNE)等,其他异质图方法也可以,但针对性不强。
模型
-
在超网络中进行随机游走来捕获顶点的高阶接近度。
- 为超网络建立了一个基本的概率模型,然后使用二阶随机游走在深度优先搜索 (DFS) 和广度优先搜索 (BFS) 之间平滑插值
- 引入了一种程度偏差随机游走机制来纠正负偏差或为随机游走引入正偏差
-
引入了对偶超网络挖掘策略,设计了一个神经网络模型来组合原始超网络和双超网络的特征,同时训练一个元组相似度函数来评估超网络中的非均匀关系。
随机游走
一阶:定义一个顶点到其邻居的转移概率
-
对于当前顶点 v,我们首先根据 e 的权重随机选择一个与 v 关联的超边 e,然后选择一个顶点 x ∈ e 作为随机游走的下一个顶点。最终形成超路径。
-
转移概率如下:
π 1 ( x ∣ v ) = ∑ e ∈ E w ( e ) h ( v , e ) d ( v ) h ( x , e ) δ ( e ) . \pi_1(x|v)=\sum_{e \in E} w(e)\frac{h(v,e)}{d(v)} \frac{h(x,e)}{\delta(e)}. π1(x∣v)=e∈E∑w(e)d(v)h(v,e)δ(e)h(x,e).
二阶:嵌入时平衡同质性和结构等价
——不仅根据当前顶点 v, 还根据**前一个顶点 u **移动到下一个顶点 x
——通过使用两个参数 p 和 q 在超网络中引入了二阶随机游走策略
-
当前顶点v的邻居分为三部分:前一个顶点 u、u 的邻居、其他顶点。
-
二阶搜索偏差 α (·) 定义如下:
α ( x ∣ v , u ) = { 1 p , if x = u 1 , if ∃ e ∈ E , x ∈ e , u ∈ e 1 q , others , \alpha(x|v,u)= \left\{ \begin{array}{l} \frac{1}{p},\space &\text{if} \space x = u \\ 1, \space &\text{if} \space \exist e \in E,x \in e,u \in e \\ \frac{1}{q}, \space &\text{others} \end{array} \right. , α(x∣v,u)=⎩ ⎨ ⎧p1, 1, q1, if x=uif ∃e∈E,x∈e,u∈eothers,
其中 p 是返回参数,它控制立即重新访问路径中前一个顶点 u 的可能性,q 是内部参数,它控制步行者探索远处还是近处的顶点。因此,二阶随机游走模型的非归一化转移概率可以表示为:
π 2 ( x ∣ v , u ) = α ( x ∣ v , u ) π 1 ( x ∣ v ) \pi_2(x|v,u)=\alpha(x|v,u)\pi_1(x|v) π2(x∣v,u)=α(x∣v,u)π1(x∣v)- q < min (p, 1)时,更倾向于访问远离u的顶点——DFS,鼓励进一步探索
- p < min (q, 1)或1 < min (p, q) 时,倾向于访问前一个顶点 u 或靠近u 的顶点——BFS,局部视图
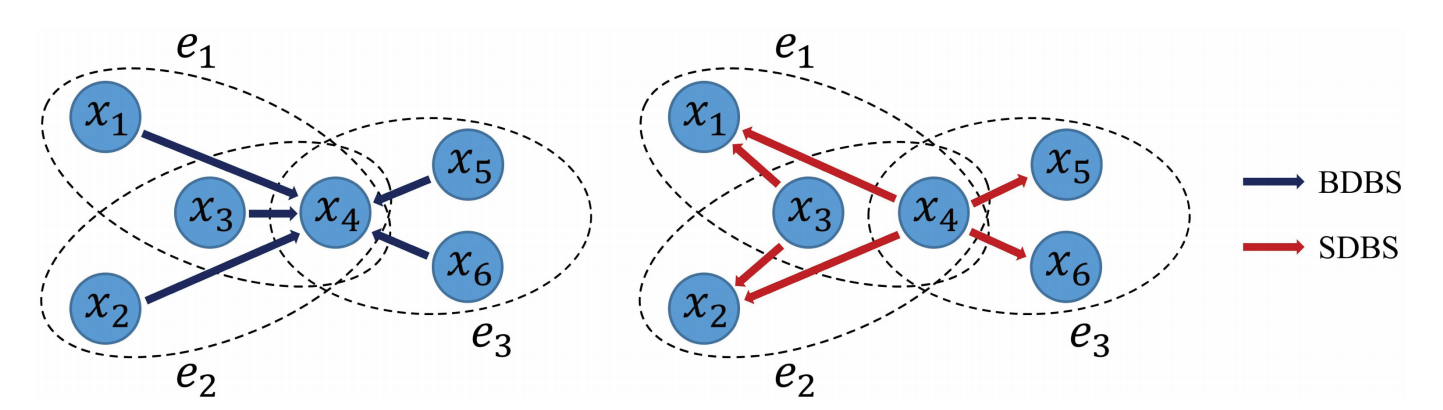
基于度的有偏随机游走:——问题:DFS 和 BFS 搜索策略将引入特定的负偏差
- 正随机游走的负偏差是有价值的
- 引入一些正偏差来捕获网络的某些特定特征或平衡顶点的更新机会也是有帮助的
——基于二阶模型,我们无法控制选择更大度或更小度的顶点。因此提出了度有偏随机游走模型:
- Big-Degree Biased Search (BDBS): 倾向于选择度数较大的邻居作为下一个顶点
- Small-Degree Biased Search (SDBS): 倾向于选择度数较小的邻居作为下一个顶点
可以看出BDBS 引导随机游走到(局部)中心,SDBS 引导随机游走到边界
——引入了一个基于 x 度的偏差系数 β ( x ) β (x) β(x),参数为 r。关键是使用 r 来控制两者之间的系数率
β ( x ) = d ( x ) + r ( r > 0 ) \beta (x)=d(x)+r \space(r>0) β(x)=d(x)+r (r>0)
顶点 x1 和 x2 的偏置系数率计算如下:
β ( x 1 ) β ( x 2 ) = d ( x 1 ) + r d ( x 2 ) + r ( r > 0 ) \frac{\beta(x_1)}{\beta(x_2)}=\frac{d(x_1)+r}{d(x_2)+r} \space (r>0) β(x2)β(x1)=d(x2)+rd(x1)+r (r>0)
显然, β ( x ) β (x ) β(x) 随 d ( x ) d (x ) d(x) 线性增长,随着 r 的增加,偏差系数率 β ( x 1 ) / β ( x 2 ) β (x1)/β (x2) β(x1)/β(x2) 比 d ( x 1 ) / d ( x 2 ) d (x1)/d (x2) d(x1)/d(x2) 平滑,这意味着 BDBS 趋势的程度下降。
SDBS (r < 0) 的策略可以类似于 BDBS。将r的不同情况组合在一起,最终公式如下:
β ( x ) = { d ( x ) + r , r > 0 1 d ( x ) − r , r < 0 1 , r = 0 . \beta(x)= \left\{ \begin{array}{l} d(x)+r,\space &r>0 \\ \frac{1}{d(x)-r}, \space &r<0 \\ 1, \space &r=0 \end{array} \right. . β(x)=⎩ ⎨ ⎧d(x)+r, d(x)−r1, 1, r>0r<0r=0.
结合之前的随机游走模型,最终转移概率 p 2 ′ ( x ∣ v , u ) p^′_2 (x |v, u) p2′(x∣v,u) 定义如下:
p 2 ′ ( x ∣ v , u ) = α ( x ∣ v , u ) ⋅ β ( x ) ⋅ ∑ e ∈ E w ( e ) h ( v , e ) d ( v ) h ( x , e ) δ ( e ) Z p^′_2 (x|v, u)=\frac{\alpha(x|v,u) \cdot \beta(x) \cdot \sum_{e \in E} w(e)\frac{h(v,e)}{d(v)} \frac{h(x,e)}{\delta(e)}}{Z} p2′(x∣v,u)=Zα(x∣v,u)⋅β(x)⋅∑e∈Ew(e)d(v)h(v,e)δ(e)h(x,e)
其中 α ( ⋅ ) α (·) α(⋅) 是二阶搜索偏差, Z Z Z 是归一化因子。基于转移概率 p 2 ′ ( x ∣ v , u ) p^′_2 (x|v, u) p2′(x∣v,u),我们可以在超网络中采样一系列顶点。
Hyper2vec算法
三部分:预处理过程、随机游走生成器、更新过程
-
预处理过程:处理超网络
- 基于一阶随机游走模型生成概率矩阵 P
- 二阶随机游走模型中由参数 p 和 q 指导概率矩阵调整
- 有偏差随机游走模型中由参数 r 指导游走偏差,进一步调整P
-
随机游走生成器:生成一组随机游走
——修改后的转移概率在预处理过程中预先计算,使用别名采样(alias sample)在 O (1) 时间内有效地完成随机游走的每一步
-
更新过程:通过 Skip-gram 模型生成最终的嵌入结果
——Skip-gram是一种语言模型,它最大化句子中彼此接近的单词之间的共现概率(此处为随机游走路径)
令 f : V → R d f : V → \mathbb R^d f:V→Rd 是从顶点到嵌入的中心映射函数, f ′ : V → R d f^′ : V → \mathbb R^d f′:V→Rd 是一个上下文映射函数, C ( v ) C (v) C(v) 是 v 的上下文,我们模型的 Skip-gram 的优化问题公式如下:
max f ∑ v ∈ V ( ∑ c i ∈ C ( v ) ( f ( v ) ⋅ f ′ ( c i ) − l o g ∑ u ∈ V e f ( v ) ⋅ f ′ ( u ) ) ) \max_f \sum_{v \in V} \left( \sum_{c_i \in C(v)} \left(f(v) \cdot f'(c_i)-log \sum_{u \in V} e^{f(v) \cdot f'(u)} \right) \right) fmaxv∈V∑ ci∈C(v)∑(f(v)⋅f′(ci)−logu∈V∑ef(v)⋅f′(u))
复杂度分析:
- 计算概率矩阵 P 的时间复杂度为 O ( a n ) O (an) O(an),其中 n 是顶点的数量,a 是每个顶点的平均邻居数(对于现实世界的网络来说通常很小);
- 对于有偏的二阶随机游走过程,存储每个顶点的邻居之间的互连很有用,最终时间复杂度为 O ( a 2 n ) O (a^2n) O(a2n);
- 随机游走过程花费 O ( t l n ) O (tln) O(tln) 时间,其中 t 是每个顶点的游走次数,l 是游走长度。
| 算法 1:Hyper2vec 算法 |
|---|
| Input:超图 G = ( V , E , w ) G = (V , E, w ) G=(V,E,w)、嵌入大小 d、窗口大小 k、行走次数 t、行走长度 l、返回参数 p、in-out 参数 q、偏置参数 r ; |
| Output:顶点表示矩阵 $\Phi \in \mathbb R^{ |
| 初始化游走为空; |
| 根据等式(1)计算转移概率矩阵 $P \in \mathbb R^{ |
| for u ∈ V u \in V u∈V do |
| ——for v ∈ N G ( u ) v \in N_G (u) v∈NG(u) do |
| ———— Π ⋅ u v ′ = β ( v ) ⋅ P u v \Pi'_{\cdot uv}=\beta(v) \cdot P_{uv} Π⋅uv′=β(v)⋅Puv; |
| ————for x ∈ N G ( v ) x \in N_G (v) x∈NG(v) do |
| ——————$\Pi’_{uvx}=\alpha(x |
| for i from 1 to t do |
| ——for v ∈ V v \in V v∈V do |
| ———— w a l k = RandomWalk ( G , Π ′ , v , l ) walk = \text{RandomWalk}(G, \Pi', v, l) walk=RandomWalk(G,Π′,v,l); |
| ————把生成的游走序列 walk 添加到 walks 列表; |
| Φ = Skip-gram ( k , d , w a l k s ) \Phi=\text{Skip-gram}(k, d, walks) Φ=Skip-gram(k,d,walks); |
| Function w a l k = RandomWalk ( G , Π ′ , v , l ) walk = \text{RandomWalk}(G, \Pi', v, l) walk=RandomWalk(G,Π′,v,l) |
| ——游走序列 walk 初始化为[s]; |
| ——前一个节点 u 初始化为null |
| ——for i from 2 to l l l do |
| ———— v = v= v= 游走序列walk的最后一个节点; |
| ———— x = AliasSample ( N G ( v ) , Π ′ u v ) ; x = \text{AliasSample}(N_G (v), \Pi′_{uv} ); x=AliasSample(NG(v),Π′uv); (别名采样算法) |
| ————把节点x添加到游走序列 walk中; |
| ———— u = v u=v u=v; |
| ——return walk; |
NHNE:对偶机制非均匀超网络嵌入
- 之前的研究只捕获了超边自己连接有哪些节点的信息(低阶信息),更详细的边缘特征(例如交互活动)可用于提高网络嵌入模型的性能;
- 本文的超网络中超边具有特别含义:文章等。使用有偏的二阶随机游走来保留顶点的高阶接近度和结构属性。
核心思想:
反转顶点和超边的定义以构建对偶超网络,使用上面的相同策略来生成对偶随机游走:
-
对偶超网络节点的嵌入对应于原始网络边的嵌入;
-
计算与 v 关联的超边的平均嵌入获得节点的嵌入。
——使用 f ∗ ( v ) f^∗ (v) f∗(v) 来表示从对偶超网络中学习到的 v 的嵌入:(加权平均)
f ∗ ( v ) = 1 ∑ e ∈ E G ( v ) w ( e ) ∑ e ∈ E G ( v ) w ( e ) ⋅ f ( e ) , f^*(v)=\frac{1}{\sum_{e\in E_G(v)}w(e)}\sum_{e\in E_G(v)}w(e)\cdot f(e), f∗(v)=∑e∈EG(v)w(e)1e∈EG(v)∑w(e)⋅f(e),
其中 f ( e ) f (e) f(e) 是从对偶超网络中学习到的超边 e 的嵌入, E G ( v ) E_G (v) EG(v) 是与 v 关联的超边集。对偶模型的过程可以与原始模型同时进行。
——从原始超网络和对偶生成的嵌入是互补的
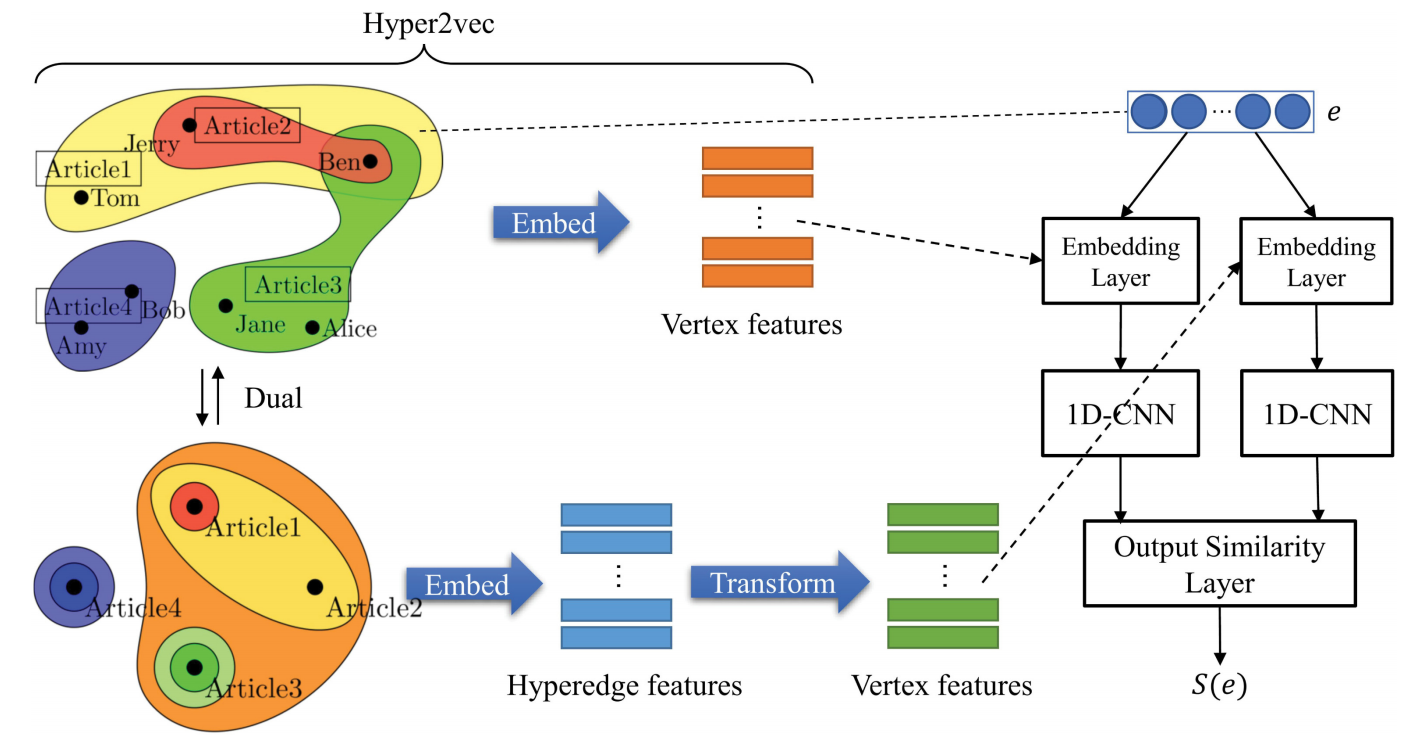
NHNE框架:
-
输入层:首先对超边(顶点集)进行编码
- 使用集合中顶点的 one-hot 编码作为超边的编码: X e = R n × z X_e=\mathbb R^{n\times z} Xe=Rn×z(n 是顶点的数量,z 是最大边度)
- 列向量是顶点的顺序,当 δ ( e ) < z δ (e) < z δ(e)<z 时,补充零向量
-
嵌入层:
- 结合嵌入层的权重, W ( e m b ) X e ∈ R d × z W^{(emb)}X_e \in \mathbb R^{d \times z} W(emb)Xe∈Rd×z 是超边 e 的初始矩阵表示
- 我们使用 Hyper2vec(原始和对偶)学习的嵌入作为嵌入层的初始权重
-
网络层:
——超网络通常是不均匀的(度不固定),超边可以看作是一个顶点序列,但顶点的顺序没有意义
- 使用一维cnn(1D-CNN)模型,表示为 c ( ⋅ ) c (\cdot) c(⋅), 由 1D 卷积层和最大池化层组成,输入 W ( e m b ) X e ∈ R d × z W^{(emb)}X_e \in \mathbb R^{d \times z} W(emb)Xe∈Rd×z,输出维度为 d 的 e 的潜在向量表示;
-
使用两个一维cnn分别捕获原始超网络和对偶超网络的隐藏信息
-
将它们连接为输出相似度层的输入
-
元组相似度函数 S (·) 定义如下:
S ( e ) = σ ( W ( o u t ) [ c o ( W o ( e m b ) X e ) ; c d ( W d ( e m b ) X e ) ] + b ) , S(e)=\sigma(W^{(out)}[c_o( W_o^{(emb)}X_e);c_d(W^{(emb )}_dX_e)]+b), S(e)=σ(W(out)[co(Wo(emb)Xe);cd(Wd(emb)Xe)]+b),
其中 σ ( ⋅ ) σ (·) σ(⋅) 是 sigmoid 函数;$ W_o^{(emb)}$ 和 W d ( e m b ) W^{(emb )}_d Wd(emb) 分别表示原始嵌入层和对偶嵌入层的权重; c o ( ⋅ ) co (·) co(⋅) 和 c d ( ⋅ ) cd (·) cd(⋅) 分别表示原始和对偶1D-CNN; W ( o u t ) W^{(out)} W(out) 表示输出相似度层的权重; b 是偏差。损失函数定义如下:
L = 1 ∣ E ∣ ∑ e ∈ E ( − log S ( e ) + ∑ e n ∈ E n log S ( e n ) ) \mathcal L=\frac{1}{|E|} \sum_{e\in E} \left(-\log S(e)+\sum_{e_n\in E_n}\log S(e_n)\right) L=∣E∣1e∈E∑(−logS(e)+en∈En∑logS(en))
其中 E n E_n En 是 e 的负样本。对于每个 e n ∈ E n e_n \in E_n en∈En , e n ∉ E e_n \notin E en∈/E 且 ∣ e n ∣ = ∣ e ∣ |e_n | = |e | ∣en∣=∣e∣。
——使用RMSProp训练模型参数
-
输出层:输出相似度层
结合嵌入层的节点嵌入,输出一个新的节点嵌入,同时输出一个元组相似度函数来评估顶点的元组关系。
与 Hyper2vec 学习的嵌入相比,NHNE 更新的嵌入包含更多关于顶点之间元组关系的特征
实验
链接预测和顶点分类两个任务
数据集:
- DBLP(合著)7,995 个顶点(作者)和 18,364 个超边(出版物)
- IMDb(参演) 4,423 个顶点(演员)和 4,433 个超边(电影)
实验设置
Hyper2vec 和 NHNE 在两个学习任务上的性能,与以下算法进行对比:
- 传统的成对网络嵌入方法:DeepWalk、Node2vec、LINE、AROPE、Metapath2vec——团扩展
- 二分网络嵌入:BiNE——星形扩展
- 超网络嵌入:HHE、HGE——(针对均匀超网络)将空顶点填充到度数小于最大度数的超边
对于所有方法,我们将嵌入大小统一设置为32。实验重复了五次。(具体各算法参数见原文)
链接预测
删除了部分边,任务是根据结果网络预测这些删除的边
顶点相似度:L1/L2距离、余弦相似度
设置:
-
DBLP:随机删除 50% 的现有超边作为正测试样本,生成相同数量的负样本(随机选择顶点,若不是超边则保留)
-
IMDB:随机删除30%
——评估AUC的大小
结果:
- Hyper2vec 优于所有基线
- NHNE 具有令人印象深刻的性能提升(原始模型和对偶模型生成的嵌入是互补的)
- BiNE、HHE 和 HGE 在链接预测任务上表现不佳
顶点分类
大多数情况下为多标签分类
设置:
按照作者/演员最多发表/参演的类型来打标签,删除一些频率非常小的类型。
逻辑回归用作外部分类器
使用Micro-F1 和 Macro-F1 来评估模型性能
结果:
- 我们的观察结果与链接预测的结果基本一致
- Hyper2vec 在分类任务上优于所有基线
- NHNE 具有令人印象深刻的性能提升
- BiNE、HHE 和 HGE 在分类任务上表现不佳
参数敏感性
对于一阶随机游走模型,最重要的一点是确保模型经过充分训练并选择适当的窗口大小
对于二阶随机游走模型,具有 DFS 趋势的随机游走在所有任务和数据集上表现更好
偏差参数 r :DBLP 超网络不需要太多度的偏差趋势,IMDb 超网络设置 r = 4
——虽然参数设置是最优的,但 Hyper2vec 无法达到 NHNE 的性能
——这意味着原始超网络没有捕获所有信息,对偶超网络提供了与原始超网络互补的信息
权重初始化的效果(略)
总结
提出了一种名为 Hyper2vec 的灵活模型来学习超网络的嵌入
- 引入了有偏的二阶随机游走策略
- 使用Skip-gram 框架进行嵌入
将对偶超网络中的超边特征结合起来构建一个名为 NHNE 的基于 1D-CNN 的模型
- 该模型有显着的改进,并在不同的任务击败了所有最先进的模型
未来工作:
参数、预测任务和超参数结构之间的更深层次的关系
更智能的参数调整机制
动态调整偏差以捕获局部属性
其他偏差指标:局部聚类系数等
更多超网络的信息:顶点和超边的属性