题目:Improving the Performance of Individually Calibrated SSVEP-BCI by Task Discriminant Component Analysis
- **1. 摘要**
- **2. 方法**
- *A.任务相关成分分析*
- *B.任务判别成分分析*
- *C.评估*
- **- 结果**
- **- 结论**
1. 摘要
脑机接口(BCI)为大脑和外部设备之间提供了一个直接通信通道。基于稳态视觉诱发电位的脑机接口(SSVEPBCI)因其高信息传输率而受到越来越多的关注。任务相关成分分析法(TRCA)是一种最新的单独校准 SSVEPBCI 的方法。然而,在 TRCA 中,从每个刺激中学习到的空间滤波器可能是冗余的,时间信息没有得到充分利用。针对这一问题,本文提出了一种新方法,即任务判别成分分析法(TDCA),以进一步提高单独校准的 SSVEPBCI 的性能。通过两个公开的基准数据集对 TDCA 的性能进行了评估,结果表明 TDCA 的性能明显优于集合 TRCA 和其他竞争方法。测试 12 名受试者的离线和在线实验进一步验证了 TDCA 的有效性。本研究为设计经过视频校准的 SSVEPBCI 解码方法提供了新的视角,并为其在高速脑拼写应用中的实现提供了启示。
2. 方法
A.任务相关成分分析
TRCA [12]是最近发展起来的一种新方法方法,来提高单独校准的SSVEPBCI 的性能。TRCA 的原理是最大限度地提高空间滤波后任务相关成分的可重复性。TRCA 的基本假设是一个生成模型,其信号模型如下:
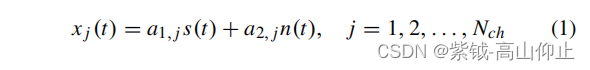

B.任务判别成分分析
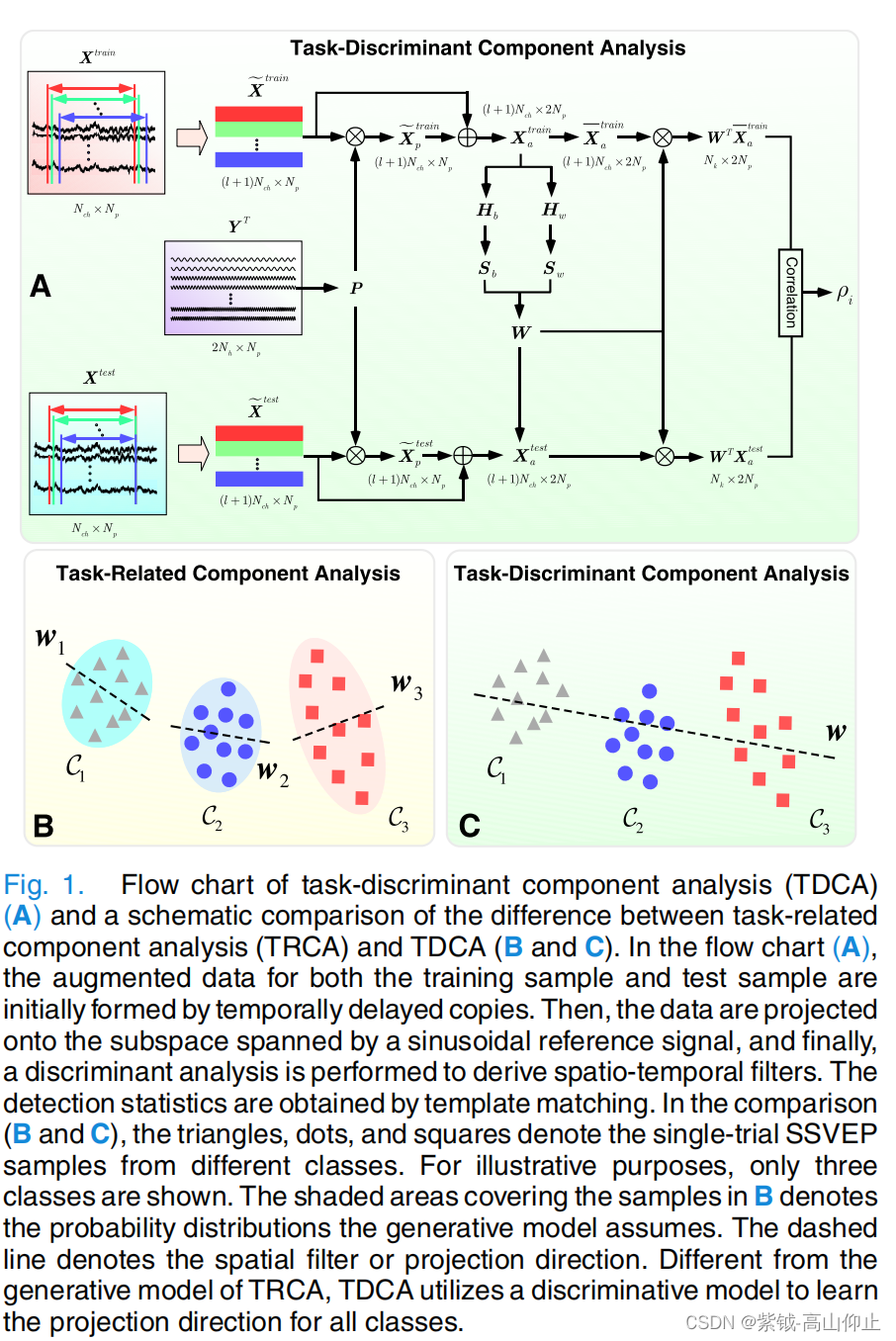
TDCA 的流程图如图 1 A 所示。图 1 B 和 C 说明了 TRCA 和建议的 TDCA 在基本假设和差异矩阵方面的区别。本研究采用的是判别模型。与针对每个类别优化空间滤波器的策略不同,本研究采用了判别分析来寻求针对所有类别的时空滤波器。下文将详细介绍拟议的 TDCA。


C.评估
1)公共数据集:TDCA 的性能最初在两个公开的 SSVEPBCI 数据集上进行了评估,即基准数据集 [23] 和 BETA 数据集 [24]。在 Benchmark 数据集上,35 名受试者在虚拟键盘的 5 8 矩阵上参加了六个区块的提示拼写任务。在 BETA 数据集中,70 名受试者参加了在 QWERTY 虚拟键盘上进行的四组提示拼写任务。两个英文字母和四个非数字符号。每个的刺激频率之一进行编码(频率间隔为 0.2 Hz): 0.2 Hz),使用联合频率和相位调制(JFPM)法[2]。基准数据集的刺激持续时间为 5 秒,BETA 数据集的刺激持续时间为 2 秒或 3 秒。64 个通道的脑电图数据由 SynAmps2(Neuroscan Inc.)两个数据集的实验条件也不同,基准数据集和 BETA 数据集分别有电磁屏蔽和无电磁屏蔽。
对公共数据集进行了四次性能评估。A) 经典蒙太奇的性能评估:在经典蒙太奇[2]中比较了 TDCA 和集合 TRCA 的性能。9个channels 在可选范围(Pz, PO3/4, PO5/6, POz, Oz, and O1/2).B)其他蒙太奇的性能评估:除经典蒙太奇外,还对 TDCA 和集合 TRCA 的其他蒙太奇配置进行了评估。这里评估了五个蒙太奇配置子集,包括中央枕蒙太奇(Nch 3、Oz、O1 和 O2)、经典枕蒙太奇(Nch 9、Pz、POz、PO3/4、PO5/6、Oz 和 O1/2)、枕蒙太奇(Nch 21、Pz、P1/2、P3/4、P5/6、Oz 和 O1/2)、 P3/4、P5/6、P7/8、POz、PO3/4、PO5/6、PO7/8、Oz、O1/2 和 CB1/2)、顶枕叶蒙太奇(Nch 30、CPz、CP1/2、CP3/4、CP5/6、TP7/8、Pz、P1/2、P3/4、P5/6、P7/8、POz、PO3/4、PO5/6、PO7/8、Oz、O1/2 和 CB1/2)以及所有通道(Nch 64)。
训练数据不足时的性能评估:在训练块(Nb)数量不同的情况下,对 TDCA 和集合 TRCA 的性能进行了评估。 具体来说,基准数据集的 Nb 从 1 到 5 不等,而 BETA 数据集的 Nb 从 1 到 3 不等。D) 与其他方法的性能比较:在与 A) 相同的设置下,TDCA 与其他具有竞争力的频率识别方法进行了比较。nition methods including multi-stimulus TRCA [13], TRCA with sine-cosine signal (TRCA-R) [14], similarity-constrainedTRCA (scTRCA) [15] 和扩展 CCA [10]。对于 B)、C)和 D)中的多重比较,进行了重复测量方差分析(RMANOVA)。当通过 Mauchly 球形度检验发现违反球形度时,则采用 GreenhouseGeisser 校正。 当发现有明显的主效应时(p < .05),则进行事后比较 t 检验,并进行 Bonferroni 校正。统计分析在 SPSS Statistics 26(IBM,Armonk,NY,USA)中进行。
在性能评估中,进行了 k 倍交叉验证,即基准数据集为 k 6,BETA 数据集为 k 4。具体来说,每个受试者的一个脑电图数据块作为测试集,其余数据作为训练集。 由于较短的数据长度对单独校准的 SSVEPBCI 至关重要,因此采用了数据长度为 Np(从 0.1 秒到 1 秒,间隔为 0.1 秒)的滑动窗口来修剪用于性能评估的历时。滑动窗口的起始时间设定为 ts d,ts d Np,ts 是视觉刺激开始的时间点。d 是根据数据集估算的延迟时间,基准数据集 [23] 的延迟时间为 140 毫秒,BETA 数据集 [24] 的延迟时间为 130 毫秒。准确度和 ITR 指标是根据每个数据长度计算得出的。以比特/分钟(bpm)为单位的 ITR 定义为 [25]:

根据先前的文献[12]、[18],对所有方法的滤波器组数 N fb 5 和组合权重进行了设置。滤波过程针对每个数据长度进行。TRCA 及其衍生方法(即 msTRCA、TRCAR 和 scTRCA)采用了集合技术[12],分别称为集合 TRCA、集合 msTRCA、集合 TRCAR 和集合 scTRCA。
我们进一步比较了 TDCA 和集合 TRCA 的潜在特征轮廓。为了描述特征空间中类别的辨别能力,我们使用离线实验数据计算了目标刺激和非目标刺激相关系数的 Rsquared 统计量[12], [26]。此外,还探讨了激活模式[27],以划分模型从数据中学到的基本空间模式。激活模式为:

2)离线实验: 我们进行了离线和在线实验,以验证所提方法对新受试者的有效性。 12 名健康受试者(6 男 6 女)参加了研究,他们的平均年龄为 23.1 ± 1.2 岁(平均标准误差,范围为 18 至 31 岁)。所有受试者视力正常或矫正视力正常。本实验获得了清华大学机构审查委员会的批准(NO.20200020),受试者在实验前提供了完全的书面同意书。
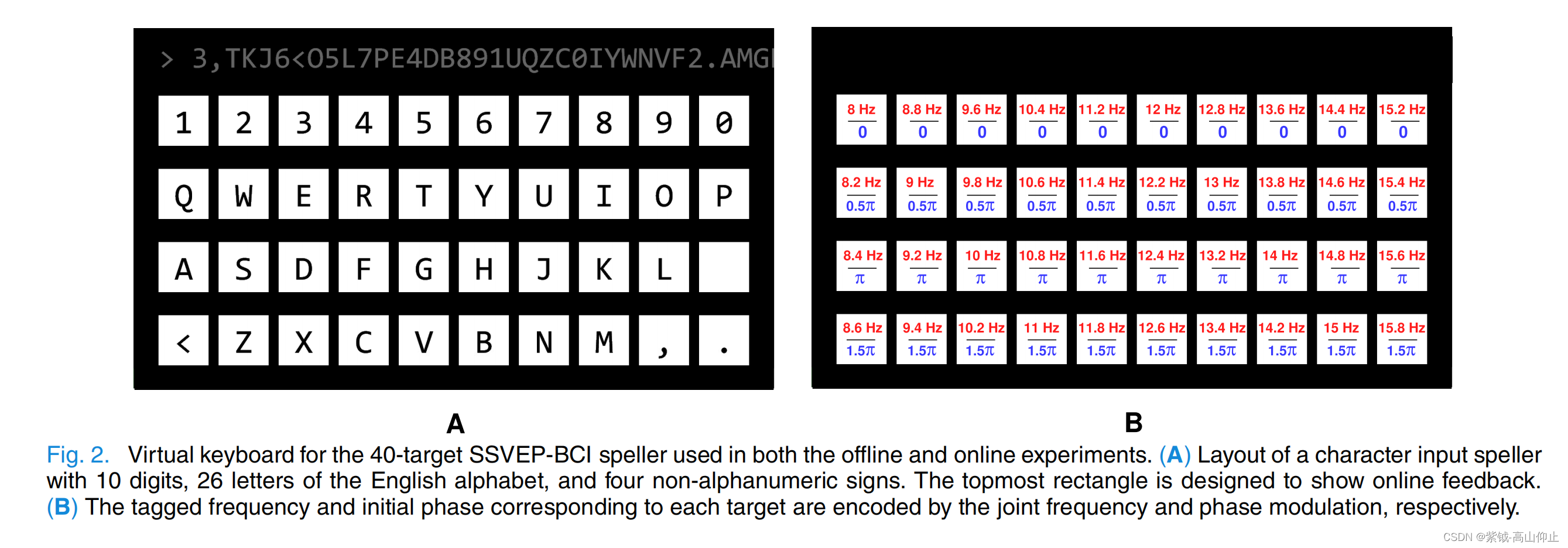
本研究设计了一个 40 个目标的虚拟拼写器,用于离线和在线实验。 如图 2 所示,虚拟拼写器上的 40 个目标(即 10 个数字、26 个英文字母和 4 个符号)被 JFPM [2] 编码为闪烁。目标的刺激频率从 8 Hz 到 15.8 Hz 不等(频率间隔为 0.2 Hz):0.2 Hz),初始相位为 0 至 1.5 π(相位间隔为 0.5 π):0.5 π).虚拟拼写器在 24.5 英寸 LED 显示器(刷新率:60 Hz)上显示:60 Hz)上显示,采用的是正弦波采样刺激法[28]。请注意,布局和编码参数与基准数据集和 BETA 数据集不同。
在离线实验中,受试者进行了一项提示拼写任务,并记录了 64 通道脑电图用于离线分析。与基准数据集一样,实验块的数量设置为六个。在每个区块中,受试者被要求将注意力集中到每个目标的中心,即在闪烁过程中,受试者被要求避免眨眼和身体移动。提示目标的顺序是随机的。为避免视觉疲劳,两个连续实验块之间有 2 分钟的间歇。
*3)在线实验:*离线实验结束后,在不同的一天进行了在线实验。具体来说,每位受试者进行了 10 个区块的提示拼写任务,包括 5 个区块的训练数据和 5 个区块的测试数据。在每个数据块中,目标提示时间为 0.5 秒,闪烁时间为 0.4 秒。在五个测试数据块中,在 0.5 秒的提示时间内,经过 TDCA 的在线分类后,拼写者会收到一个反馈。九个枕叶通道(Pz、POz、PO3/4、PO5/6、Oz 和 O1/2)的经典蒙太奇被记录下来,用于计算在线分类准确率和 ITR。
离线和在线实验中的脑电图数据都是在电磁屏蔽室中通过无线放大器(Neurcle,中国)采集的,触发器通过并行端口同步。应用无限脉冲响应(IIR)陷波滤波器去除电力线的干扰,离线和在线分析的数据被降采样至 250 Hz。除 Nk 7 和 l 5 参数外,性能评估程序与基准数据集一致。视觉演示是在 MATLAB(MathWorks, Inc.)
- 结果
图 3 展示了利用公共数据集(A 和 B. 基准数据集)评估的 TDCA 和集合 TRCA 的平均分类准确率和 ITR 性能: A 和 B:基准数据集;C 和 D:BETA 数据集)。结果显示,在所有数据长度下,TDCA 的表现都优于集合 TRCA。在 0.5 秒时,TDCA 的最高 ITR 为 244.34± 10.84 bpm,而对于集合 TRCA,0.5 秒时的最高 ITR 为219.67 ±12.47 bpm。配对 t 检验显示在所有数据长度上,TRCA 和 TDCA 的准确度差异均有统计学意义(p < .05),而在 ITR 上,数据长度大于 0.1 秒时,TRCA 和 TDCA 的准确度差异也有统计学意义(p < .05)。 对于 0.5 秒的数据长度,TDCA 和集合 TRCA 的准确度分别为 0.850±0.027 和 0.794 ±0.033,差异为0.057 (p < .001).具体来说,在 94.3% 的受试者中,TDCA 比 TRCA 更具优势,而 TRCA 和 TDCA 的结果见图 3。
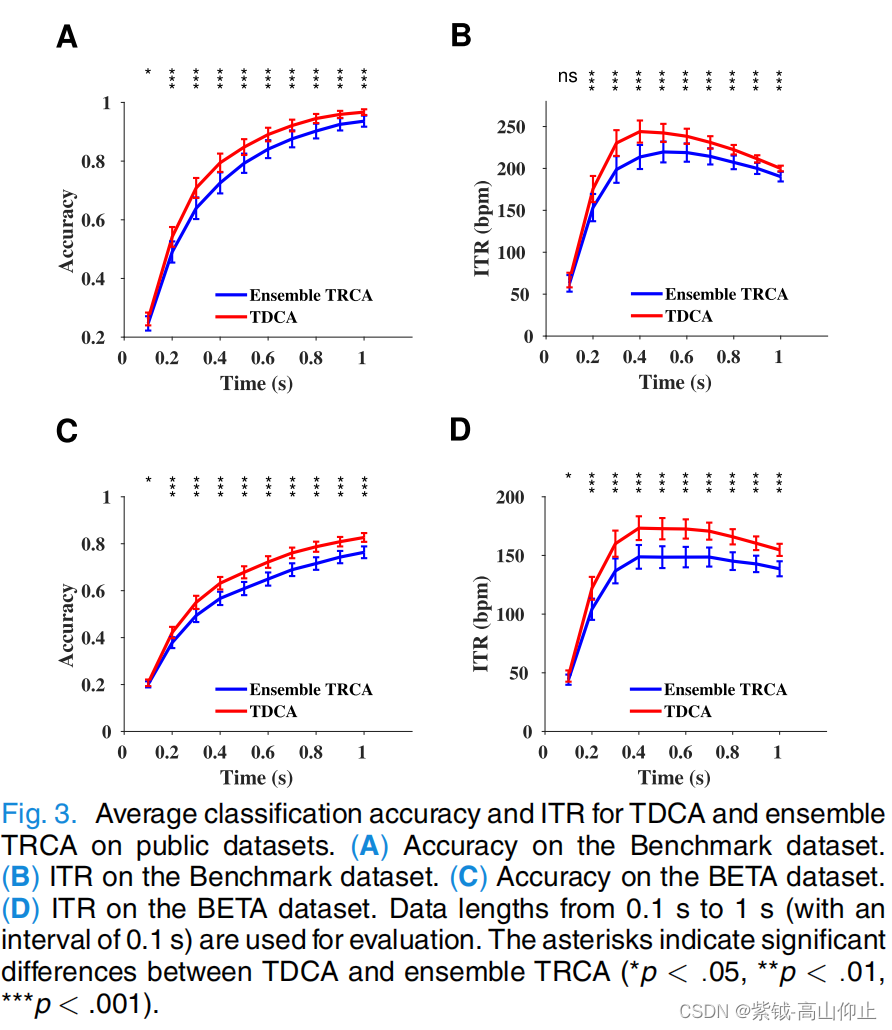
一些有代表性的受试者详见补充表 1。在数据长度为 1 秒时,TDCA 和集合 TRCA 的准确度分别为 0.968 ± 0.010 和 0.936 ± 0.019,差异为 0.032(p =.002)。

在 BETA 数据集上,TDCA 的表现明显优于集合 TRCA(参见图 3 C 和 D)。 图 3 C 和 D)。TDCA 和集合 TRCA 的最高 ITR 分别为 174.88 ± 10.19 bpm(0.4 秒)和 148.81 ± 10.13 bpm(0.4 秒)、和 148.81 ± 10.13 bpm(0.4 秒)。对于超过 0.1 秒的数据长度,配对 t 检验显示,TDCA 和集合 TRCA 在准确度和 ITR 方面的差异均有统计学意义(p < .05)。在数据长度为 0.5 秒时,TDCA 和集合 TRCA 的准确度分别为 0.680 ± 0.028 和 0.609 ± 0.028,差异为 0.070(p < .001)。具体来说,91.4% 的受试者的 TDCA 比 TRCA 更有优势,一些代表性受试者的结果详见补充表 II。在数据长度为 1 秒时,TDCA 的准确率为TDCA 和集合 TRCA 分别为 0.826 ± 0.019 和 0.764 ± 0.025,差异为 0.063(p < .001)。
图 4 展示了不同蒙太奇对 TDCA 和集合 TRCA 的影响(A:基准数据集;B:BETA 数据集)。在这里,每种方法的性能都是通过跨数据长度的最大平均 ITR 来衡量的。根据双向(方法-蒙太奇)重复测量方差分析(RMANOVA)的评估,方法与蒙太奇之间的交互作用在基准数据集和 BETA 数据集上都具有显著的统计学意义,基准数据集的交互作用为 F(2.399,81.556)=15.335,P < .001,GreenhouseGeisser 校正;BETA 数据集的交互作F(2.905,200.441)=30.097,P < .001,GreenhouseGeisser 校正。 配对 t 检验显示,在两个数据集的不同蒙太奇上,TDCA 都明显优于 ensem ble TRCA(p < .001)。值得注意的是,在 TDCA 和集合 TRCA 中,经典蒙太奇并不是产生最高 ITR 的最佳蒙太奇。在 TDCA 中,基准数据集的最佳蒙太奇是顶枕蒙太奇(TDCA:280.47 ± 10.64 bpm; ensemble TRCA:239.23 ± 14.52 bpm; p < .001),而 BETA 数据集的枕骨蒙太奇(TDCA:197.72 ± 10.24 bpm; ensemble TRCA:164.91 ± 10.91 bpm;p < .001)。当通道数超过最佳蒙太奇时,TDCA 和集合 TRCA 的 ITR 显著下降,尤其是集合 TRCA。
图 5 显示了 TDCA 和集合 TRCA 在不同训练块数量下的最大平均 ITR。双向(方法块)RMANOVA 发现,在统计上存在显著的块主效应对基准数据集的主效应具有统计学意义,F(1.29,43.859) = 324.455,对于 BETA 数据集,F(1.067,73.629) =272.329,p < .001, Greenhouse Geisser 校正。随着训练块数量的增加,TDCA 和集合 TRCA 的性能都有所提高,在两个数据集上,TDCA 的性能始终显著优于集合 TRCA(p < .001)。例如,在训练数据不足三个块的情况下,TDCA 在基准数据集上的性能为 219.7 ± 8.75 bpm,而集合 TRCA 为 191.64 ± 11.06 bpm;在 BETA 数据集上,TDCA 的性能为 173.31 ± 10.13 bpm,而集合 TRCA 为 148.81 ± 10.11 bpm。
各种竞争方法与 TDCA 的性能比较见图 6(A:基准数据集;B:BETA 数据集)。在这里,每种方法的性能还表现在最大平均 ITR 值上。
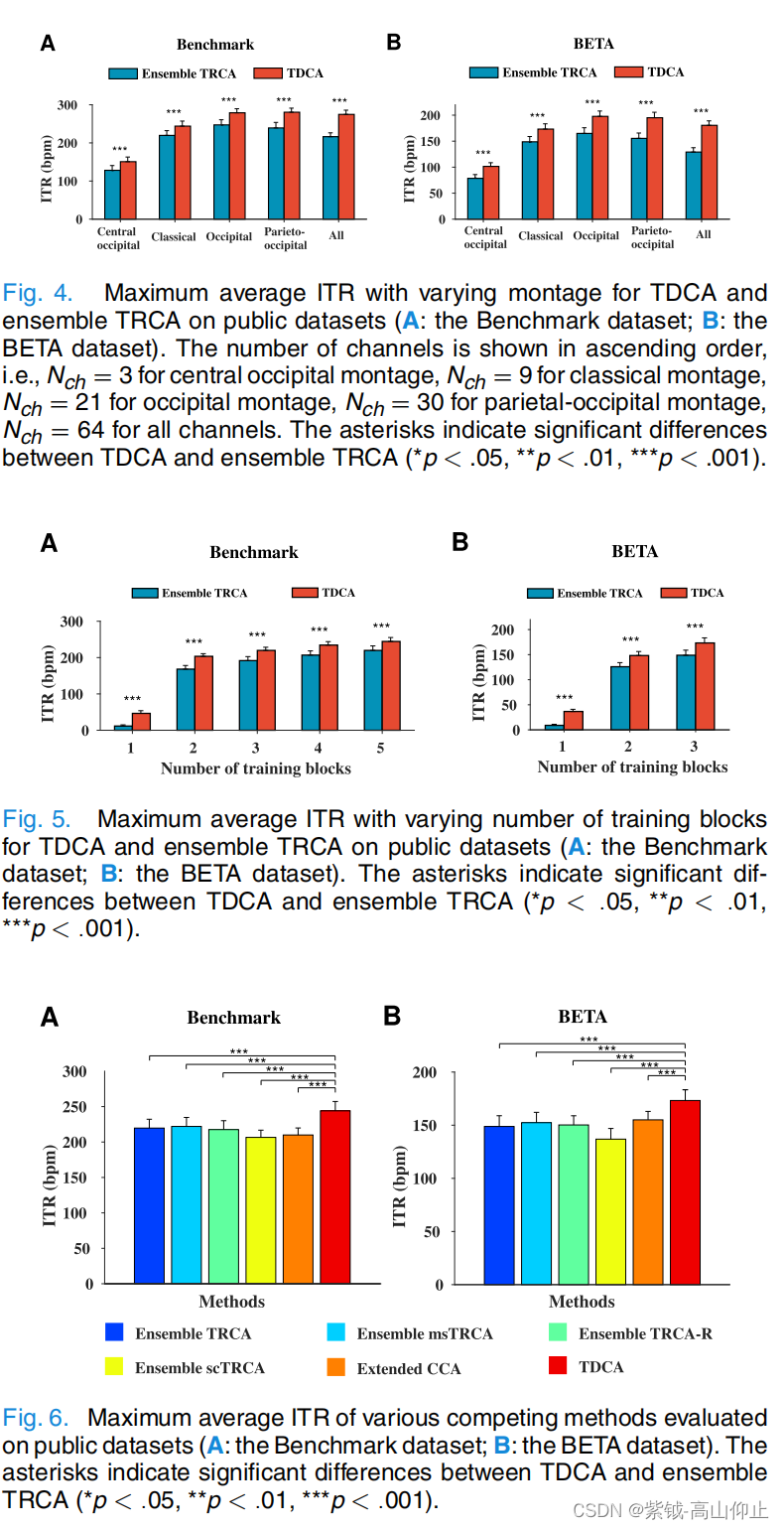
在所有数据长度上都是如此。与图 3 所示的比较结果一致,在所有比较方法中,TDCA 在基准数据集和 BETA 数据集上都取得了最高的性能。单向 RMANOVA 显示,在基准数据集上,比较方法之间存在显著的统计学差异,F(1.822,61.939) = 22.408,p < .001,Greenhouse Geisser 校正;在 BETA 数据集上,比较方法之间存在显著的统计学差异,F(3.365,232.169) = 31.217,p < .001,Greenhouse Geisser 校正。经 Bonferroni 校正的配对 tt 检验发现,在两个数据集上,TDCA 与其他每种方法之间都存在显著的统计学差异(p < .001)。在其他比较方法中,性能最好的方法是 msTRCA(用于基准数据集)和扩展 CCA(用于 BETA 数据集),前者的最大平均 ITR 为 222.00 ± 12.68 bpm,后者的最大平均 ITR 为 155.04 ± 7.94 bpm。下文将进一步介绍特征空间的概况。如图 7 所示,当数据长度超过 0.1 秒时,TDCA 的 Rsquared 值明显超过集合 TRCA 的 Rsquared 值(p < .001)。 例如,在数据长度为 1 秒时,Rsquared 从集合 TRCA 的 0.454 ± 0.057 增加到 TDCA 的 0.547 ± 0.052,从而提高了分类准确率和 ITR [16],[17]。此外,图 8 显示了从公共数据集中学习的 TDCA 和集合 TRCA 的平均激活模式,其中划定了激活模式的第一部分。在这里,TRCA 是对所有类别和受试者进行平均,而 TDCA 则是对所有受试者进行平均。与集合 TRCA 相比,目测结果表明,在基准数据集(图 8B)和 BETA 数据集(图 8D)中,TDCA 的激活模式在枕叶区域的分布更加密集和对称。在集合 TRCA 中,额叶和颞叶区域均可发现权重较高的分散激活,而在 TDCA 中,额叶和颞叶区域的激活权重较低,在这些区域被抑制。
在离线实验中,12 个实验对象的平均分类准确率和 ITR 如图 9 所示。与公共数据集上的结果一致,TDCA 在准确率和 ITR 方面的表现均高于 TRCA 组合。
配对 t 检验发现,数据长度超过 0.1 秒时,差异有统计学意义(p < .01)。在数据长度为 0.4 秒时,两种方法都达到了最高的 ITR,即 TDCA 为 232.13 ± 20.05 bpm,而集合 TRCA 为 200.82 ± 21.58 bpm,p < .001。 在数据长度为 1 秒时,TDCA 和集合 TRCA 的精确度分别为 0.917± 0.026 和 0.875 ± 0.037,差异为 0.042(p .006)。图 10 展示了在线实验中 TDCA 与集合 TRCA 的性能对比。TDCA 的平均在线准确率为 0.82 ± 0.04,明显高于集合 TRCA 的准确率 0.72 0.06(p .001)。因此,在在线 ITR 方面,TDCA 明显优于集合 TRCA(TDCA:251.8 ± 17.9 bpm; ensemble TRCA: 207.4 ± 25.3 bpm;P 6.14 × 10-4)。表 I 总结了个体 ITR 的详细情况。 在个体水平上,结果
显示,TDCA 对 BCI 性能较差的受试者(如 S3 和 S4)的改善更大。然而,对于 BCI 性能出色的受试者(如 S12 和 S7),TDCA 只带来了微不足道的改善,并出现了天花板效应。


- 结论
本研究提出了一种新的频率识别方法,即任务判别成分分析法(TDCA),以改进频率识别的性能。在 TDCA 中,从数据中学习共同的时空滤波器,以判别的方式学习。因此,模型无需逐类学习投影方向。与集合 TRCA 不同,TDCA 不需要集合技术。我们在两个基准数据集、一个离线实验和一个在线实验上进行了广泛的验证,从而验证了 TDCA 的有效性。这些验证结果表明,TDCA 优于集合 TRCA 和其他竞争方法。本研究为 TDCA 方法的扩展奠定了基础,并指出了其在高速脑拼读器中的潜在应用前景。



![算法:合并两个有序数组---双指针[1]](https://img-blog.csdnimg.cn/901cb5a6d22247e4a1b2fcb20c6adfe5.png#pic_center)