【如无特别说明,皆为最小二叉堆】
1 介绍

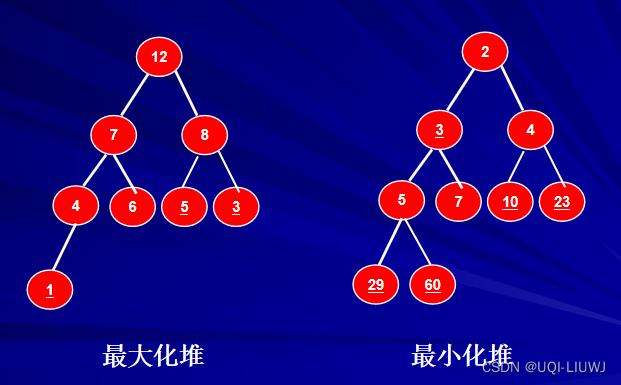
2 特性
- 结构性:符合完全二叉树的结构
- 有序性:满足父节点小于子节点(最小化堆)或父节点大于子节点(最大化堆)
3 二叉堆的存储
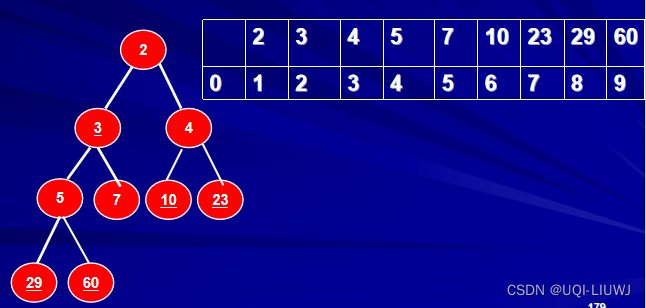
顺序存储
二叉堆的有序性可以很容易地通过下标来反映
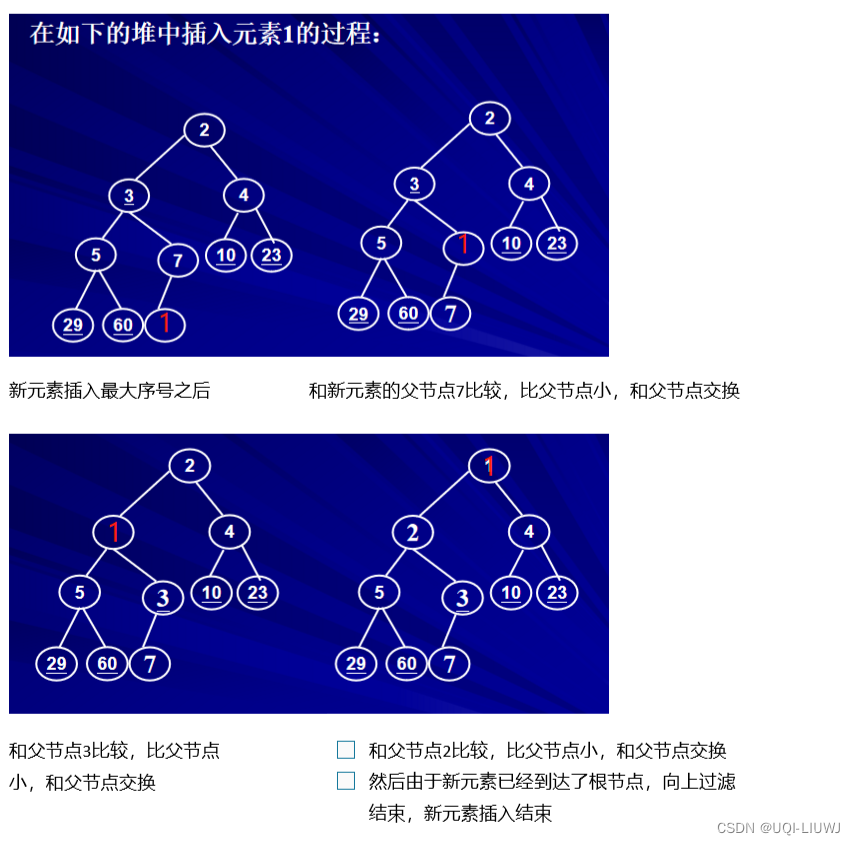
4 堆中插入新元素
- 堆的插入是在具有最大序号的元素之后插入新的元素或结点,否则将违反堆的结构性。
- 如果新元素放入后,没有违反堆的有序性,那么操作结束。
- 否则,让该节点向父节点移动,直到满足有序性或到达根节点。
- 新节点的向上移动称为向上过滤
4.1 时间效率
- 最坏情况是O(logn) 【一直交换到根节点】
- 平均情况,过滤会提前结束。
- 有资料表明,平均是2.6次比较,因此元素平均上移1.6层。
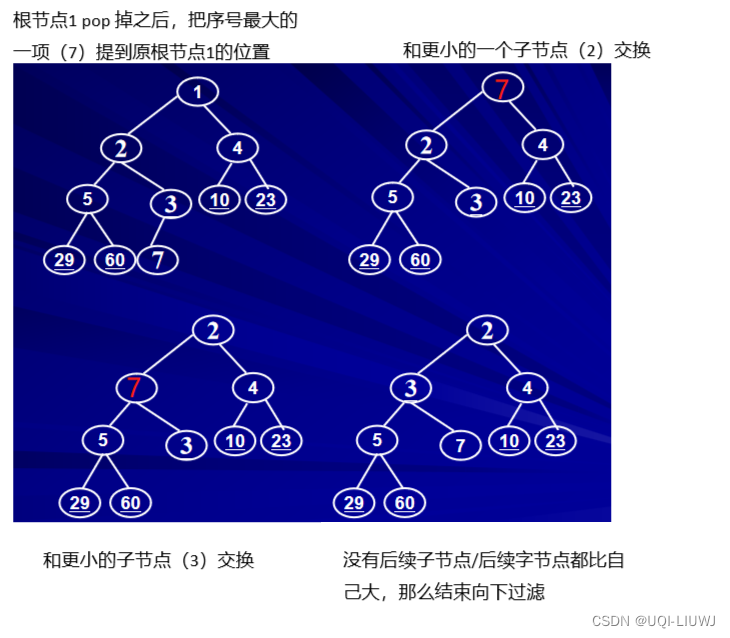
5 推出操作(DeQueue)
- 当最小元素被删除时,在根上出现了一个空结点。堆的大小比以前小1,堆的结构性告诉我们,最后一个结点应该删掉。
- 如果最后一项可以放在此空结点中,就把它放进去。然而,这通常是不可能的
- 必须玩与插入操作类似的“游戏”:把某些项放入空结点,然后移动空结点。
- 仅有的区别在于:对DeQueue操作,空结点是往下移动。
- 找到空结点的一个较小的子结点,如果该儿子的值小于我们要放入的项,则把该儿子放入空结点,把空结点往下推一层
- 重复这个动作,直到该项能被放入正确的位置。
5.1 时间复杂度
- 最坏情况下,deQueue是一个对数时间的操作
- 根据堆的有序性,堆中最后一个结点的值一般都是比较大的。因此,向下过滤很少有提前一或二层结束的,所以deQueue操作平均也是对数时间
6 建堆
- 可以看成N次连续插入,其时间应该是在O(NlogN)时间内完成
- 事实上,在构造过程中,我们并不关心每个元素加入后堆的状态,我们关心的是N个元素全部加入后的最后状态,最后的状态是要保证堆的有序性。至于中间过程中的有序性是否成立并不重要。
- 有了这个前提后,我们能将构造堆的时间复杂度降到O(N)
- 利用堆的递归定义
- 如果函数buildHeap可以将一棵完全二叉树调整为一个堆 ,那么,只要对左子堆和右子堆递归调用buildHeap。
- 至此,我们能保证除了根结点外,其余的地方都建立起了堆的有序性。
- 然后对根结点调用向下过滤,以创建堆的有序性
- 如果我们以逆向层次的次序对结点调用向下过滤,那么在向下过滤节点i时,所有结点i的子孙都已经调用过向下过滤。
- 不需要对叶结点执行向下过滤
- 从编号最大的非叶结点开始向下过滤
- 利用堆的递归定义
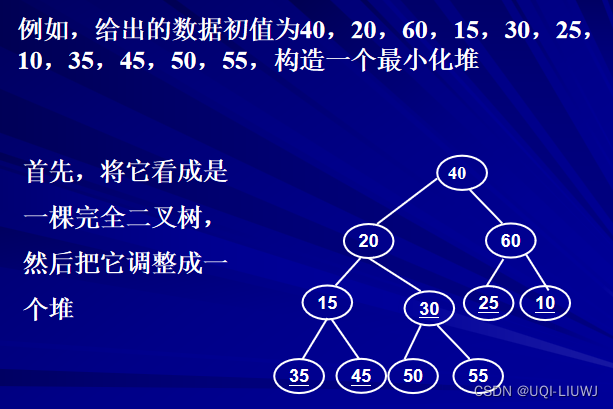
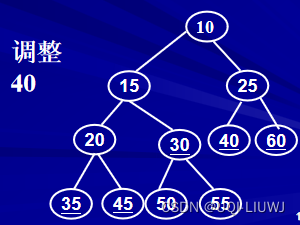
6.1 举例
一开始根据数据的先后建立一棵完全二叉树
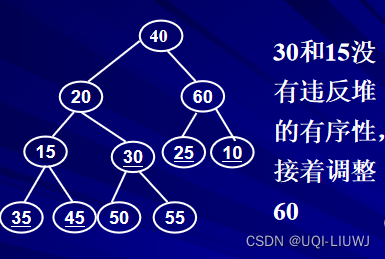
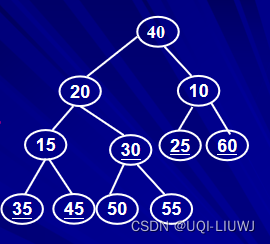
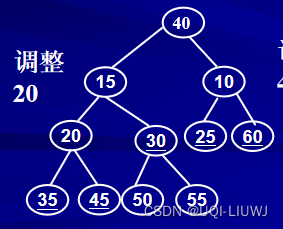
从序号最大的非叶子节点(30)开始进行向下过滤
6.2 时间分析
- 为h的节点(叶节点高度为0),在向下过滤中交换的最大次数是h
- 建堆的最大时间是所有节点的调整时所需交换次数之和,即所有节点的高度之和

7 D堆
- 每个节点有d个儿子,这样生成的堆比较矮。
- 插入:
- 删除:需要在d个元素中找出最小的,时间复杂度为:
- 优点:插入快
- 缺点:删除慢
- 用途:
- 插入比删除多的队列
- 队列太大,内存放不下,要放在外存的时候