目录

1.算法流程简介

2.算法核心代码

3.算法效果展示

1.算法流程简介

#二次规划模型
#二次规划我们需要用到函数:Cvxopt.solvers.qp(P,q,G,h,A,b)
#首先解决二次规划问题和解决线性规划问题的流程差不多
"""
求解思路如下:
1.针对给定的代求式,转化成标准式子
2.根据转化后的式子,求出矩阵P,q,G,h,A,b
3.代入Cvxopt.solvers.qp(P,q,G,h,A,b)中,求出答案即可
#ps:答案给出的是字典型的,需要进行转化
"""
"""
#Question1:min 2x1^2+x2^2+x1x2+x1+x2s.t.:x1>=0x2>=0x1+x2=1
转化成标准形式:min 2x1^2+x2^2+x1x2+x1+x2s.t.:-x1<=0-x2<=0x1+x2=1
"""

2.算法核心代码

#2.根据标准式给出矩阵集
import pprint
from cvxopt import matrix,solvers
P=matrix([[4.0,1.0],[1.0,2.0]])
q=matrix([1.0,1.0])
G=matrix([[-1.0,0.0],[0.0,-1.0]])
h=matrix([0.0,0.0])
A = matrix([[1.0],[1.0]])
b=matrix([1.0])
ans=solvers.qp(P,q,G,h,A,b)
print("x的解如下所示:")
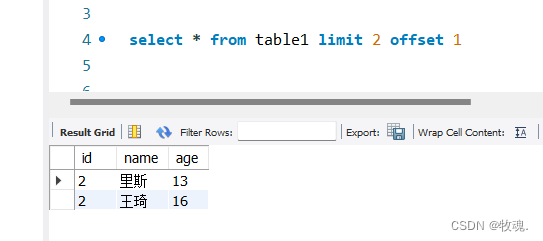
print(ans['x'])

3.算法效果展示