2023高教社杯数学建模国赛的工具箱准备
数学建模国赛工具箱(私信领取)!!!小编仔细阅读了比赛官方网站上的规则和要求,以及比赛的题型和时间安排,现总结分享给大家。欢迎私信和评论,有问必答,有干货必分享!!!
这是小编总结的一些代码和资料(本文中的代码以及参考书籍等)
代码资料:https://github.com/HuaandQi/Mathematical-modeling.git
①学习优秀论文–了解建模、算法、写作方面的最佳实践;
②学习优秀算法–模型复杂、求解困难、算力要求高;
③制作写作模板–好的写作等于成功的一半;
④学会查阅最新文献–传统算法+最新算法+自创算法;
⑤分工协作,选好做题方向–三个臭皮匠,顶个诸葛亮。
1.数学建模国赛的题型攻略及算法汇总
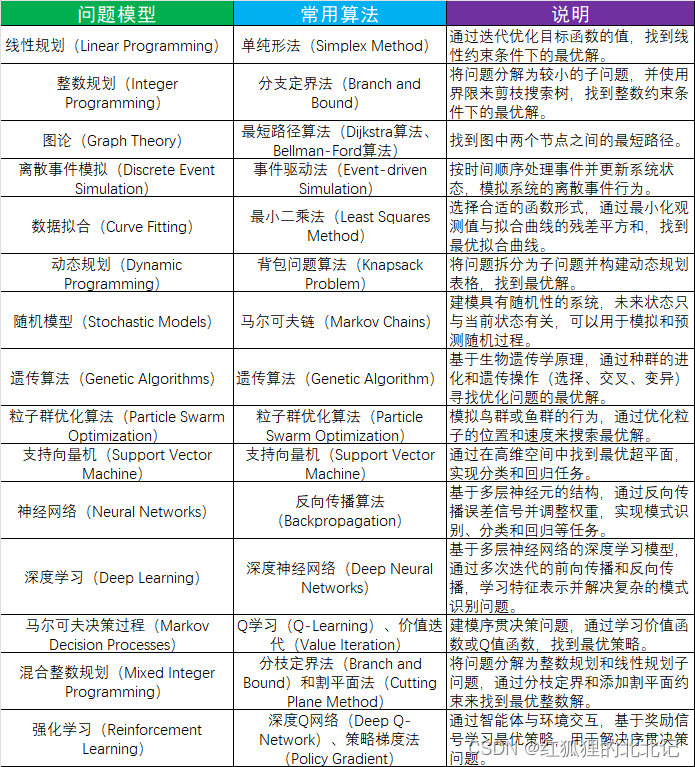
数学建模国赛的题型包括ABCDE五类,主要可以分为以下几种类型问题:
① 连续型数学建模问题:
连续型数学建模问题通常涉及数学模型的建立、求解和分析,其中连续函数和微积分等数学概念是关键。例如,优化问题、微分方程建模等。
②离散型数学建模问题:
离散型数学建模问题涉及到离散数据、概率统计、组合数学等离散数学领域的知识。例如,排队论、图论问题、组合优化等。
③仿真建模问题:
仿真建模问题要求建立一个模拟系统来模拟实际情况,并进行模拟实验。这种类型的问题可能需要使用建模软件来创建虚拟环境。例如,蒙特卡洛模拟、离散事件仿真等。
④数据分析和机器学习问题:
这类问题要求分析给定的数据集或者使用机器学习算法来预测未来趋势。机器学习、数据挖掘和统计分析等技术在这类问题中得到广泛应用。
⑤混合型问题:
混合型问题结合了上述不同类型的要素,可能需要综合运用多种数学建模方法。这类问题通常更具挑战性。
⑥工程实践问题:
这类问题通常基于实际工程问题,要求解决具体的工程挑战。例如,交通流量优化、供应链管理、电力系统规划等。
⑦社会科学建模问题:
这类问题与社会、经济、环境等领域的现实问题相关,需要结合相关领域知识建立数学模型,以解决社会问题。
针对不同类型的问题,我们可以使用不同的算法:
2.优秀论文
优秀的论文可以给我们提供非常明确的解题思路,大家在解题的过程中一定要结合之前的优秀论文进行辅助,这样会让你更得心应手。
优秀论文链接:http://www.mathclub.top/
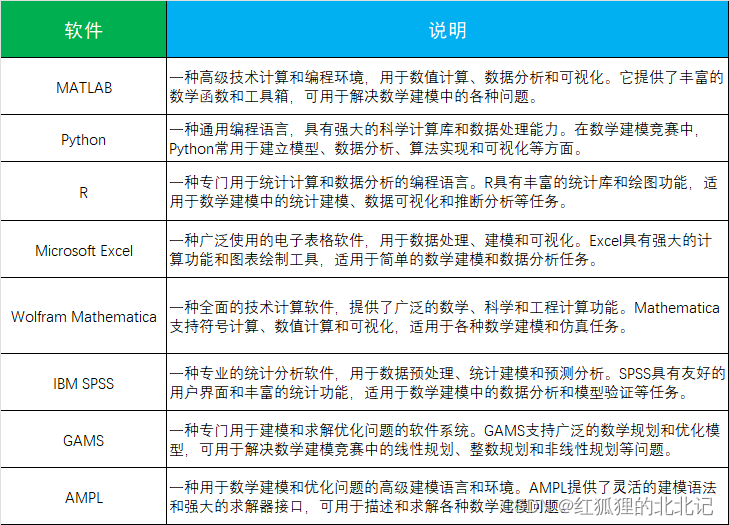
3.写作软件
熟悉掌握排版软件可以让我们节省非常多的时间和精力,从而可以有更多的精力去解题,这些是推荐的写作软件,可以提前准备一下哦!

4.编程、计算软件
大家可以根据自己擅长的语言进行选择,关于很多工具箱,小编后面也会更新到链接上面,提供给大家参考!
5.知识储备
①数学方面:对于高等数学有一定的了解,比如求解方程组,数据处理中的归一化,方差,标准差,矩阵运算,积分求解,解高次方程,行列式求解,微分方程建立于求解等等。当然,最好也学过一些计算数学方面的知识。总之,这方面的知识越多,对模型的建立帮助就越大。不过,对于本科期间的建模,所需要的数学知识并不多深。
②编程方面:在编程语言发展过程中,出现的语言有几千种,如今比较常用的有C语言(面向过程),python(面向对象),matlab(专用于数学计算)等等。对于C语言,个人认为,在建模中不建议用,主要原因是编程太复杂,且数据多时,对C语言不精通的人编写的语言往往非常慢。对于python,我认为不错,它的numpy,pandas,matplotlib库等库专为计算而生,对于计算非常友好,而且易于编程,对于一些新手非常适合。最后的matlab可以说与python差不多,也适用于计算,而且语法更为简单,同时,功能也非常强大。所以,python和matlab在建模中都是比较适合的
③写作方面:对于word必须非常熟悉,尤其是插入公式,排版等,同时,最好学会latex(专业的论文写作排版软件)。还有,学会各种表述,比如问题分析如何表述,问题求解如何表述等等。总之,就是要达到能把复杂概念用简单易懂的语句表述出来。
④算法方面:至少要知道且会运用各种插值方法,多元线性(非线性)回归,灰色预测,动态规划,贪心算法,层次分析,微分方程与偏微分方程,整数规划,排队论,时间序列分析,因子分析,动力系统,差分,最好再会设计神经网络。对于求解,则要会梯度下降,牛顿类算法等等。
⑤学习途径:中国大学mooc平台,B站(本人常用)等等,主要是要找到适合自己的课程,并且坚持下去。
6.比赛过程
①拿到问题,三个人先独自分析,找出问题的关键,然后讨论交流,确定题目;
②专注于确定的题目,通过搜索相关资料,确定问题意图,建立初步模型(如果一天后,仍然没有一丝进展,果断换题)
③集全队之力,对初步模型进行修改,然后求解。
④解决一问,就写一问的论文,与解题速度保持同步。
⑤最后一点就是:不要丧气,不要丧气,不要丧气!保持积极的心态。