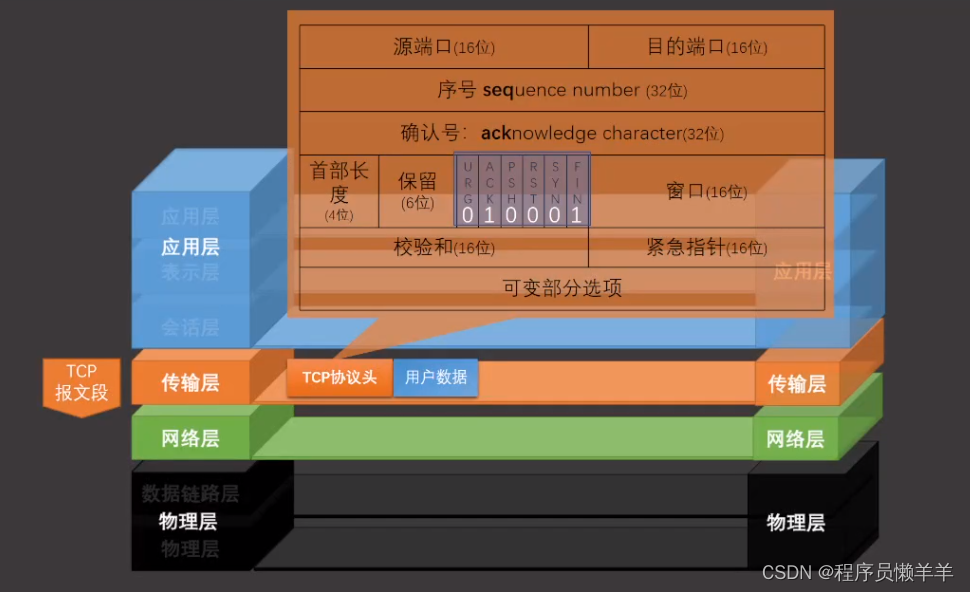
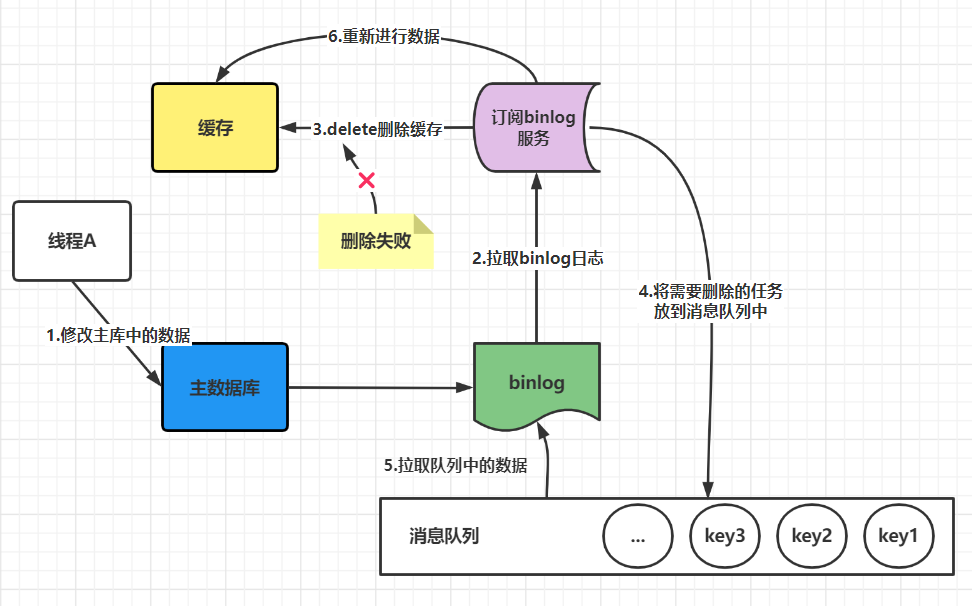
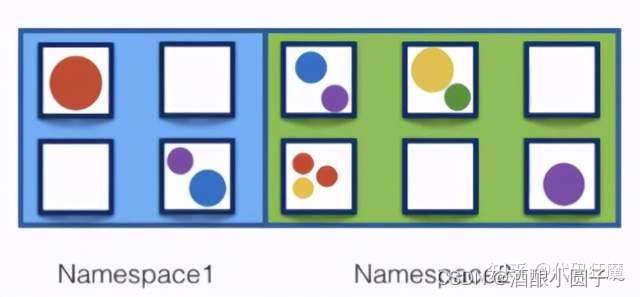
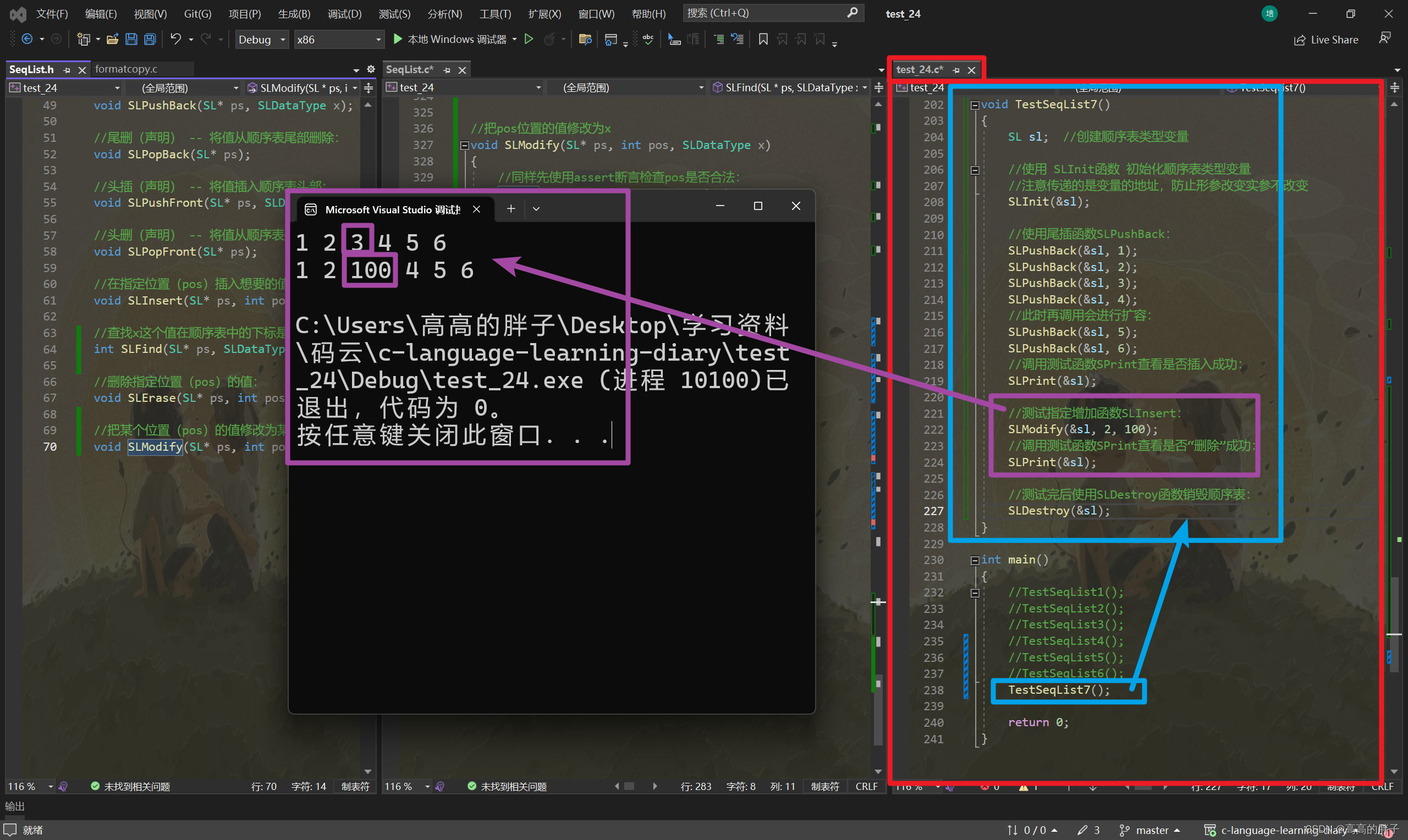
大家来看以下几个结构：下图中的结构除了一颗不是树其余的都是，我们可以发现这个跟我们现实生活的树是不是非常相似.

在树形结构里面有几个重要的术语：

1.结点：树里面的元素。

2.父子关系：结点之间相连的边

3.子树：当结点大于1时，其余的结点分为的互不相交的集合称为子树

4.度：一个结点拥有的子树数量称为结点的度

5.叶子：度为0的结点

6.孩子：结点的子树的根称为孩子结点

7.双亲：和孩子结点对应

8.兄弟：同一个双亲结点

9.森林：由N个互不相交的树构成深林

在树形结构里面有几个重要的术语：

结点的高度：结点到叶子结点的最长路径

结点的深度：根结点到该结点的边个数

结点的层数：结点的深度加1

树的高度：根结点的高度

常见的二叉树：平衡二叉树 二叉查找树 红黑树 完全二叉树：（堆排序；大顶堆，小顶堆） 满二叉树

常见的N叉树：B树（B-Tree，B+Tree）

在树形结构中最重要的就是二叉树，很多经典的算法与数据结构其实都是通过二叉树发展而来。        

        Binary Tree:一种特殊的树形结构，每个节点至多只有两颗子树。

        在二叉树的第N层上至多有2^(N-1)个结点。最多有2^N-1个结点个数。

        满二叉树：除叶子结点外，每个结点都有左右两个子结点。

        完全二叉树：除最后一层外，其他的结点个数必须达到最大，并且最后一层结点都连续靠左排列。

思考？为什么要分满二叉树和完全二叉树呢？因为通过定义可以看出，完全二叉树只是满二叉树里面的一个子集

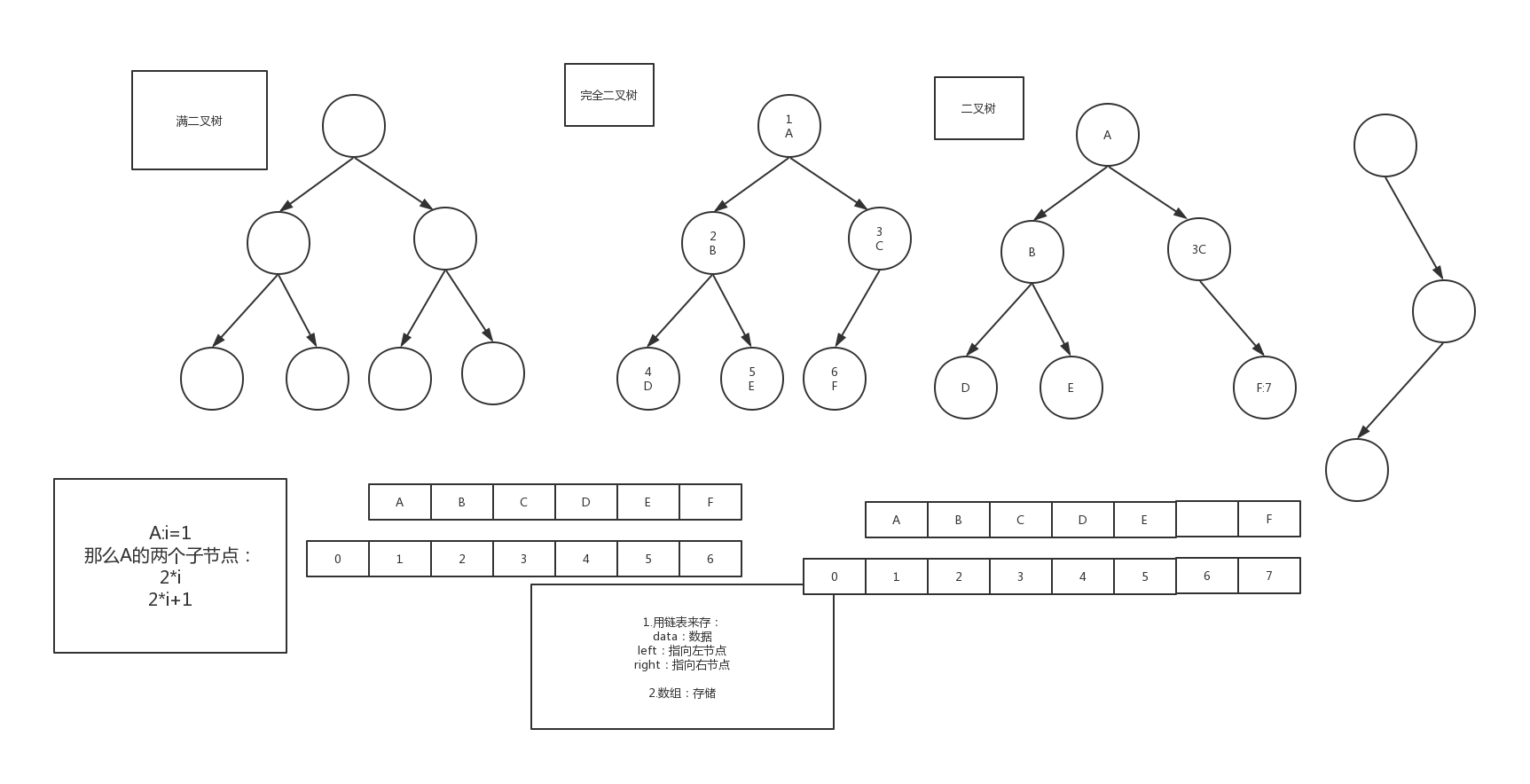
要想清楚上面那个问题我们要从树形结构的存储开始：

        基于数组存储：利用数组下标。假设A为i，则B=2*i,C=2*i+1，依次类推 但是假如是下面第二图这种情况，用数组存储会发生什么情况？

        答：你会发现如果用数组来存储的话会浪费很多空间，那怎么办呢？大家最先想到的肯定是链表，对的， 是要借用链表来实现，但是数组的性能是高效的，也不需要开额外的指针，所以如果是一课完全 二叉树的话我们就可以用数组来实现，因为可以使用数组下标和结点对应，如上图。如果不是完全二叉树的话如果缺失左叶子，只有右叶子的话数组存储会浪费空间。这也是为什么还要分一个完全二叉树出来的根本原因。 后面的堆还会在来看这个结构。

四种遍历方式： 

        重要口诀：根节点输出！子树

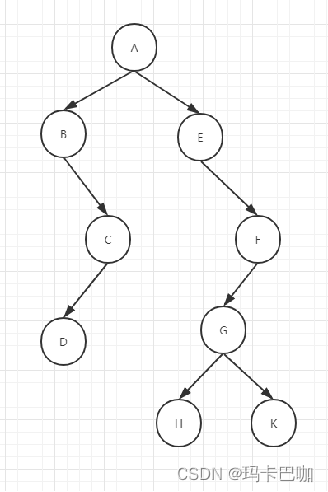
        前序：根 左 右

        中序：左 根 右 BDCAEHGKF

        后序：左 右 根  DCBHKGFEA

注意：每次遍历从根结点开始算，然后将根下方的看成一个子树，然后按照口诀根输出遍历，遇到根输出就行！

代码实现树

package tree;class MyTreeNode{private char data;private MyTreeNode left;private MyTreeNode right;public MyTreeNode(char data, MyTreeNode left, MyTreeNode right) {super();this.setData(data);this.setLeft(left);this.setRight(right);}public char getData() {return data;}public void setData(char data) {this.data = data;}public MyTreeNode getLeft() {return left;}public void setLeft(MyTreeNode left) {this.left = left;}public MyTreeNode getRight() {return right;}public void setRight(MyTreeNode right) {this.right = right;}}public class BinaryTree {public static void main(String[] args) {MyTreeNode D = new MyTreeNode('D', null, null);MyTreeNode H = new MyTreeNode('H', null, null);MyTreeNode K = new MyTreeNode('K', null, null);MyTreeNode C = new MyTreeNode('C', D, null);MyTreeNode G = new MyTreeNode('G', H, K);MyTreeNode B = new MyTreeNode('B', null, C);MyTreeNode F = new MyTreeNode('F', G, null);MyTreeNode E = new MyTreeNode('E', null, F);MyTreeNode A = new MyTreeNode('A', B, E);BinaryTree binaryTree = new BinaryTree();System.out.println("前");binaryTree.pre(A);System.out.println();System.out.println("中");binaryTree.in(A);System.out.println();System.out.println("后");binaryTree.post(A);}public void print(MyTreeNode node){System.out.print(node.getData());}public void pre(MyTreeNode root){		//前序遍历 根(输出) 左 右 时间复杂度？O(n) N^2 O(2*n)=>O(n);print(root);if(root.getLeft() != null){pre(root.getLeft());	//认为是子树,分解子问题；}if(root.getRight() != null){pre(root.getRight());}}public void in(MyTreeNode root){		//中序遍历  左 根(输出)  右if(root.getLeft() != null){in(root.getLeft());	//认为是子树,分解子问题；}print(root);if(root.getRight() != null){in(root.getRight());}}public void post(MyTreeNode root){		//后序遍历  左  右 根(输出) if(root.getLeft() != null){post(root.getLeft());	//认为是子树,分解子问题；}if(root.getRight() != null){post(root.getRight());}print(root);}
}