正弦信号的平均功率和峰值电压计算举例
一、问题
假设加载在纯电阻为R=1Ω,频率为50Hz和60Hz的正弦信号的平均功率分别为0.5W和2W,请求解这两个信号的峰值电压 U p 1 U_{p1} Up1和 U p 2 U_{p2} Up2。
二、解答:
根据欧姆定律可知:对于纯电阻R两端的瞬时电流为
I = U R = U p s i n ( 2 π f t ) R (1) I=\frac{U}{R}=\frac{U_{p}sin(2\pi ft)}{R}\tag{1} I=RU=RUpsin(2πft)(1)
根据功率计算公式,则瞬时功率P为:
P = U I = U 2 R = [ U p s i n ( 2 π f t ) ] 2 R (2) P=UI=\frac{U^2}{R}=\frac{ { [U_{p}sin(2\pi ft)} ]^2 } {R}\tag{2} P=UI=RU2=R[Upsin(2πft)]2(2)
若求解平均功率 P ‾ \overline P P,根据式(2)可得:
P ‾ = 1 T ∫ 0 T [ U p sin ( 2 π f t ) ] 2 R d t (3) \overline P = \frac{1}{T}\int_0^T {\frac{{{{[{U_p}\sin (2\pi ft)]}^2}}}{R}dt} \tag{3} P=T1∫0TR[Upsin(2πft)]2dt(3)
进一步,得到
P ‾ = 1 T ∫ 0 T [ U p sin ( 2 π f t ) ] 2 R d t = U p 2 T R ∫ 0 T [ sin ( 2 π f t ) ] 2 d t (4) \overline P = \frac{1}{T}\int_0^T {\frac{{{{[{U_p}\sin (2\pi ft)]}^2}}}{R}dt} \\= \frac{{U_p^2}}{{TR}}\int_0^T {{{[\sin (2\pi ft)]}^2}dt} \tag{4} P=T1∫0TR[Upsin(2πft)]2dt=TRUp2∫0T[sin(2πft)]2dt(4)
又由于 ∫ 0 T [ sin ( 2 π f t ) ] 2 d t \int_0^T {{{[\sin (2\pi ft)]}^2}dt} ∫0T[sin(2πft)]2dt可通过下面计算
T 2 − sin ( 4 π f T ) 8 π f (5) \dfrac{T}{2}-\dfrac{\sin\left(4\,\pi\,f\,T\right)}{8\,\pi\,f} \tag{5} 2T−8πfsin(4πfT)(5)
若取 T T T为正弦信号的一个周期,则 T = 1 / f T=1/f T=1/f,那么式(5)得到:
T 2 − sin ( 4 π ) 8 π f = T 2 (6) \dfrac{T}{2}-\dfrac{\sin\left(4\,\pi\right)}{8\,\pi\,f}=\frac{T}{2} \tag{6} 2T−8πfsin(4π)=2T(6)
将式子(6)带入式子(4)得到:
P ‾ = 1 T ∫ 0 T [ U p sin ( 2 π f t ) ] 2 R d t = U p 2 T R ∫ 0 T [ sin ( 2 π f t ) ] 2 d t = U p 2 T R T 2 = U p 2 2 R (7) \overline P = \frac{1}{T}\int_0^T {\frac{{{{[{U_p}\sin (2\pi ft)]}^2}}}{R}dt} \\= \frac{{U_p^2}}{{TR}}\int_0^T {{{[\sin (2\pi ft)]}^2}dt} \\=\frac{{U_p^2}}{{TR}} \frac{T}{2} \\=\frac{{U_p^2}}{{2R}} \tag{7} P=T1∫0TR[Upsin(2πft)]2dt=TRUp2∫0T[sin(2πft)]2dt=TRUp22T=2RUp2(7)
根据题设若R=1欧姆,平均功率分别为0.5瓦特和2瓦特,则带入式子(7)得到:
0.5 W = U p 1 2 2 ⋅ 1 Ω (8a) 0.5W=\frac{U^2_{p1}}{2\cdot1Ω} \tag{8a} 0.5W=2⋅1ΩUp12(8a)
2 W = U p 2 2 2 ⋅ 1 Ω (8b) 2W=\frac{U^2_{p2}}{2 \cdot 1Ω} \tag{8b} 2W=2⋅1ΩUp22(8b)
根据式子(8a)和(8b)可得:
U p 1 = 1 V (9a) U_{p1}=1V \tag{9a} Up1=1V(9a)
U p 2 = 2 V (9b) U_{p2}=2V \tag{9b} Up2=2V(9b)
综上分析计算可得:加载在纯电阻为R=1Ω,频率为50Hz和60Hz的正弦信号的平均功率分别为0.5W和2W,请求解这两个信号的峰值电压 U p 1 U_{p1} Up1和$U_{p2}分别为1V和2V.
三、仿真
根据上面的分析,编写程序,进行仿真。
编写的程序如下:
clc
clear all
close allFs=1000;
dt=1/Fs;
t=0:dt:0.1;U1=sin(2*pi*50*t);
U2=2*sin(2*pi*60*t);
figure(20230908)
subplot(2,2,1)
plot(t,U1,'b',"LineWidth",2)
xlabel('Time [s]')
ylabel('Voltage [V]')
title('Subplot 1: U1=sin(2*pi*50*t)')subplot(2,2,2)
plot(t,U2,'g',"LineWidth",2)
xlabel('Time [s]')
ylabel('Voltage [V]')
title('Subplot 2: U2=2*sin(2*pi*60*t)')subplot(2,2,[3,4])
plot(t,U1,'b',t,U2,'g',"LineWidth",2)
xlabel('Time [s]')
ylabel('Voltage [V]')
legend("U1","U2")
title('Subplot 3 and 4: Both')运行结果:如图1所示。
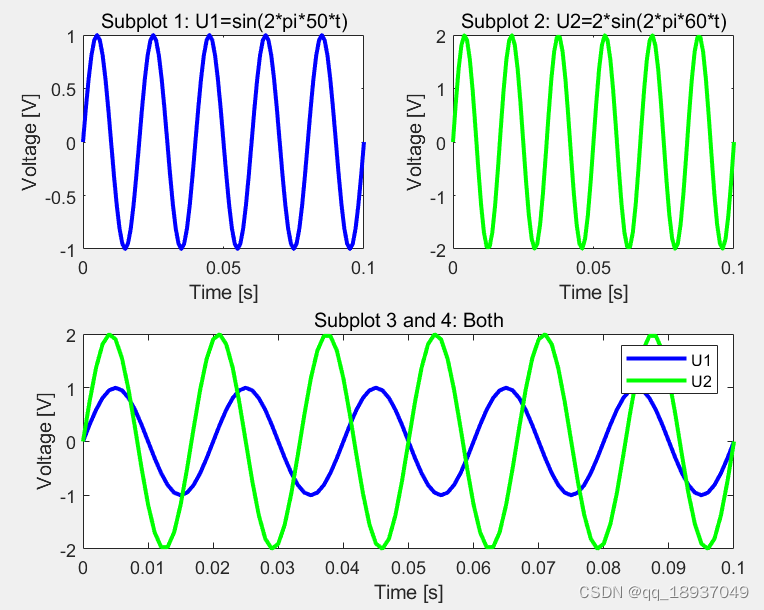
图1 仿真得到两个正弦信号