Matlab 如何选择采样频率和信号长度

1、概述

在实际信号分析中经常会遇到要分辨出频率间隔为 $f_{\delta }$ 的两个分量，在这种情形中如何选择采样频率和信号的长度呢？

2、案例分析

设有一个信号 $x(t)$ 由三个正弦信号组成，其频率分别为 $f_{1}=1Hz, f_{2}=2.5Hz, f_{1}=3Hz$ ，即： $x(t)=sin(2*pi*f_{1}*t)+sin(2*pi*f_{2}*t)+sin(2*pi*f_{3}*t)$

下面介绍如何选择采样频率 $f_{s}$ 和信号长度 N 。

因为信号的最高频率 $f_{c}$ 为 3Hz，故按采样定理 $f_{s}\geqslant 2*f_{c}=6$ ，选择 $f_{s}=10Hz$ ，由频域分辨率分析可知，若要分辨 1Hz 和 2.5Hz的频率分量，最小采样长度 N1必须满足 $N_{1}\geqslant \frac{f_{s}}{\Delta f_{min}}=\frac{10}{2.5-1}=6.6$

若要区分 2.5Hz 和 3Hz 的频率分量，则最小采样长度 N2 必须为 $N_{2} \geqslant \frac{f_{s}}{\Delta f_{min}}=\frac{10}{3-2.5}=20$

因此，为了能区分各频率的峰值，信号的最小长度应为20。

3、实例

例：某信号由三个正弦信号组成，频率分别为 $f_{1}=1Hz, f_{2}=2.5Hz, f_{1}=3Hz$ ，采样频率

$f_{s}=10Hz$ ，分别以数据长度 $N=20, 40, 128$ 来分析该信号。

% Matlab 如何选择采样频率和信号长度
% 
% pr2_2_10  clear; clc; close all;M = 256; % 数据长度M
fs = 10; % 采样频率fs
f1 = 1; f2 = 2.5; f3 = 3; % 设置3个正弦信号的频率
t = (0:M-1)/fs; % 设置时间序列
x = cos(2*pi*f1*t)+cos(2*pi*f2*t)+cos(2*pi*f3*t); % 计算出信号波形X1 = fft(x,20); % FFT变换
X2 = fft(x,40);
X3 = fft(x,128);
freq1 = (0:10)*fs/20; % 计算3个信号在频域的频率刻度
freq2 = (0:20)*fs/40;
freq3 = (0:64)*fs/128;% 作图
plot(freq1,abs(X1(1:11)),'g--',freq2,abs(X2(1:21)),'r:',freq3,abs(X3(1:65)),'b-');
legend('N=20','N=40','N=128');
title('不同N值的DFT变换');
xlabel('频率/Hz'); 
ylabel('幅值');
set(gcf,'color','w');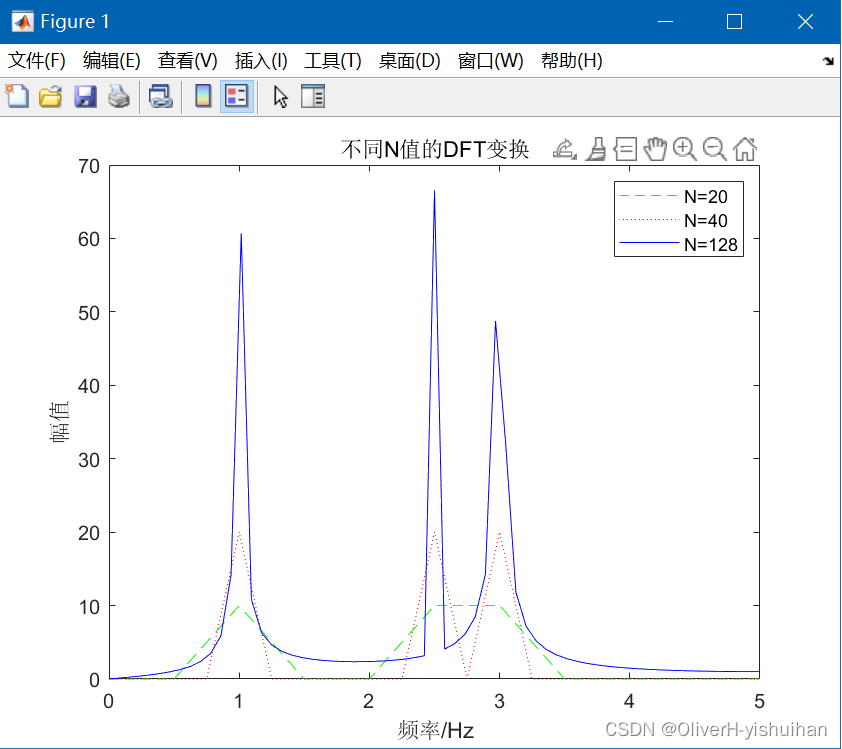

从图中可以看出，当 N=20 点时，虽然 2.5Hz 和 3Hz 这两个峰值大致能分开，但还是不太明显，可以认为是两个峰值，也可能被误认为有一个峰值在这两点之间。当 N=40 点时这两个峰值就十分明显了，因为 N 增加一倍后在这两点之间增加了一个谷值，从而突出了峰值。当 N=128 时，峰值更明显了，但由于栅栏现象和矩形窗泄漏存在，3个正弦信号虽然输入时幅值相同，但从频域上反映出的幅值各不相同。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/126089.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！