资料:
课程网址
斯坦福CS224W图机器学习、图神经网络、知识图谱【同济子豪兄】
斯坦福大学CS224W图机器学习公开课-同济子豪兄中文精讲
图的基本表示
图是描述各种关联现象的通用语言。与传统数据分析中的样本服从独立同分布假设不一样,图数据自带关联结构,数据和数据,样本和样本之间有联系。
图神经网络是端到端的表示学习,无需人工特征工程,可以自动学习特征(类似CNN)。
图神经网络的目标是实现图嵌入,即将一个节点映射成d维向量,同时保证网络中相似的节点有相近的向量表示。这个d维向量应该包含节点在原图中的结构信息,语意信息,以方便后续的数据挖掘。
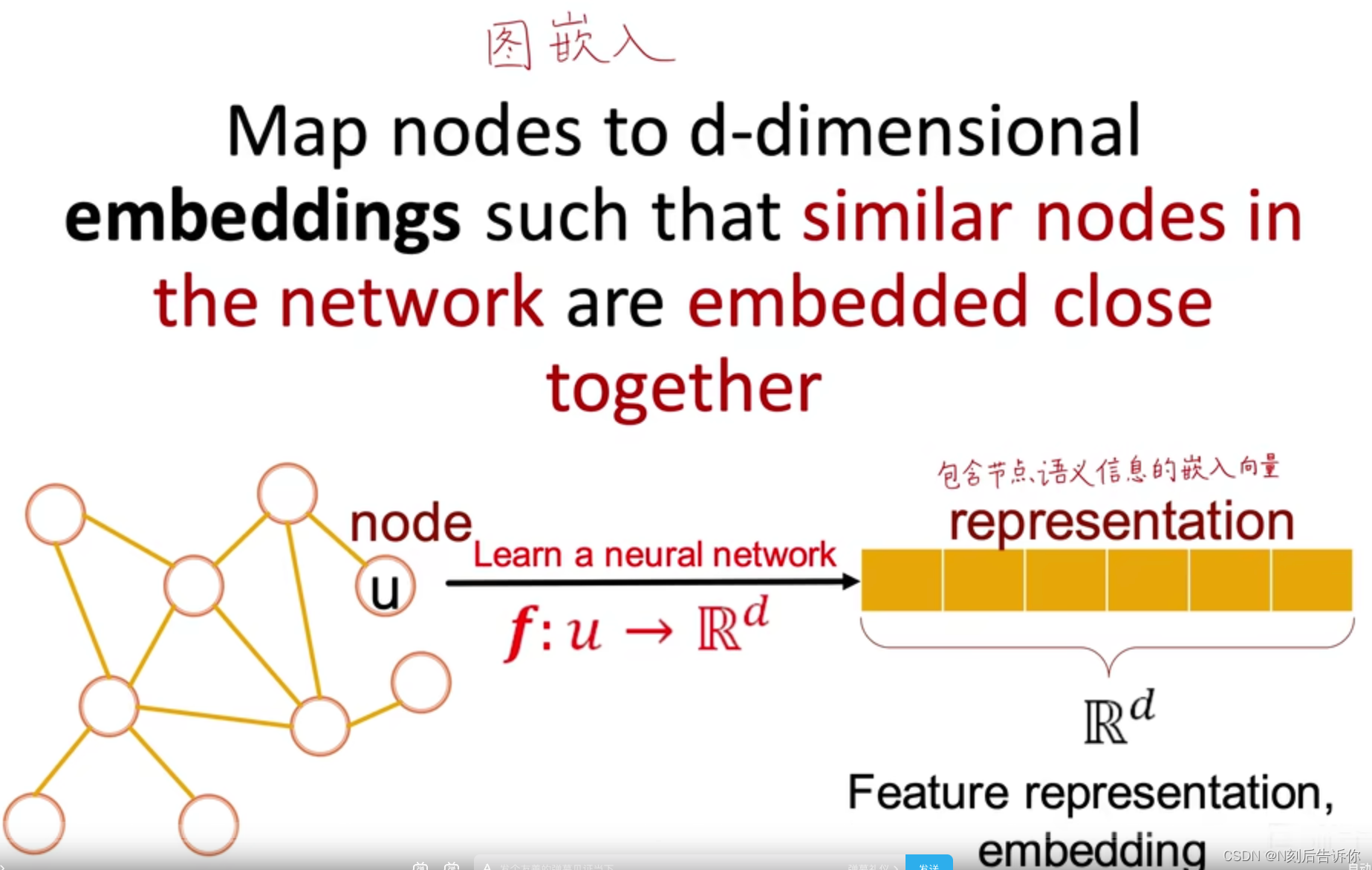
节点、连接、子图、全图都可以带有特征
不同的任务
在节点、连接、子图、全图层面,都可以进行图数据挖掘
- 节点层面的案例:如信用卡欺诈
- 连接层面的案例:如推荐可能认识的人
- 子图层面的案例:如用户聚类
- 全图层面的案例:全图层面的预测,如分子是否有毒;全图层面的生成,如生成新的分子结构
图的本体设计
图(network/graph)由节点(nodes/vertices)和连接(links/edges)组成。
节点的集合用
N表示,连接的集合用E表示,整个图用G(N,E)表示。
本体图
图的设计牵涉到一个概念,本体图(Ontology)。本体图应该显示节点可能的类型,以及各类型节点(包括节点类型到其自身)之间可能存在的关系。如下图,是一个医疗领域的知识图谱的本体图。
如何设计本体图,取决于要解决的问题。如下图,例如要解决的问题是,什么疾病可以吃什么,那么疾病和食物就需要设计成节点。可以吃,不可以吃, 不推荐吃就应该设计成节点之间的关系
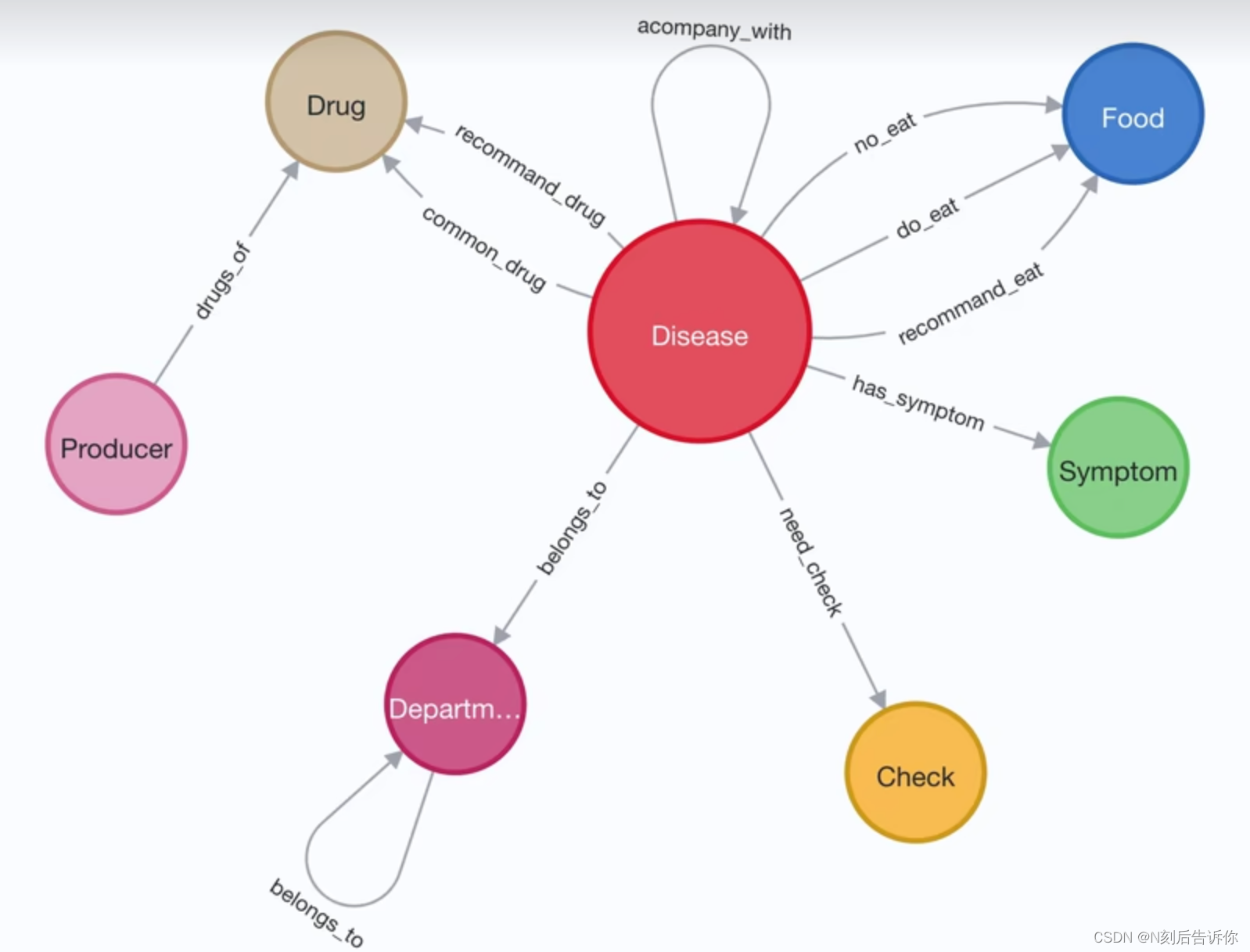
有时本体图是唯一、无歧义的,如社交网络
有时本体图不唯一,取决于你要研究的问题,如考虑红楼梦的家族,地点,事件等
图的种类(有向、无向、异质、二分、连接带权重)
图可以分为无向图、有向图、异质图(heterogeneous graph)、二分图。
- 无向图:对称的、双向的图。如合作关系,facebook上的好友关系
- 有向图:单向的图。如电话,Twitter上的关注
- 异质图:节点和连接可能有不同的类型,是很多论文研究的重点
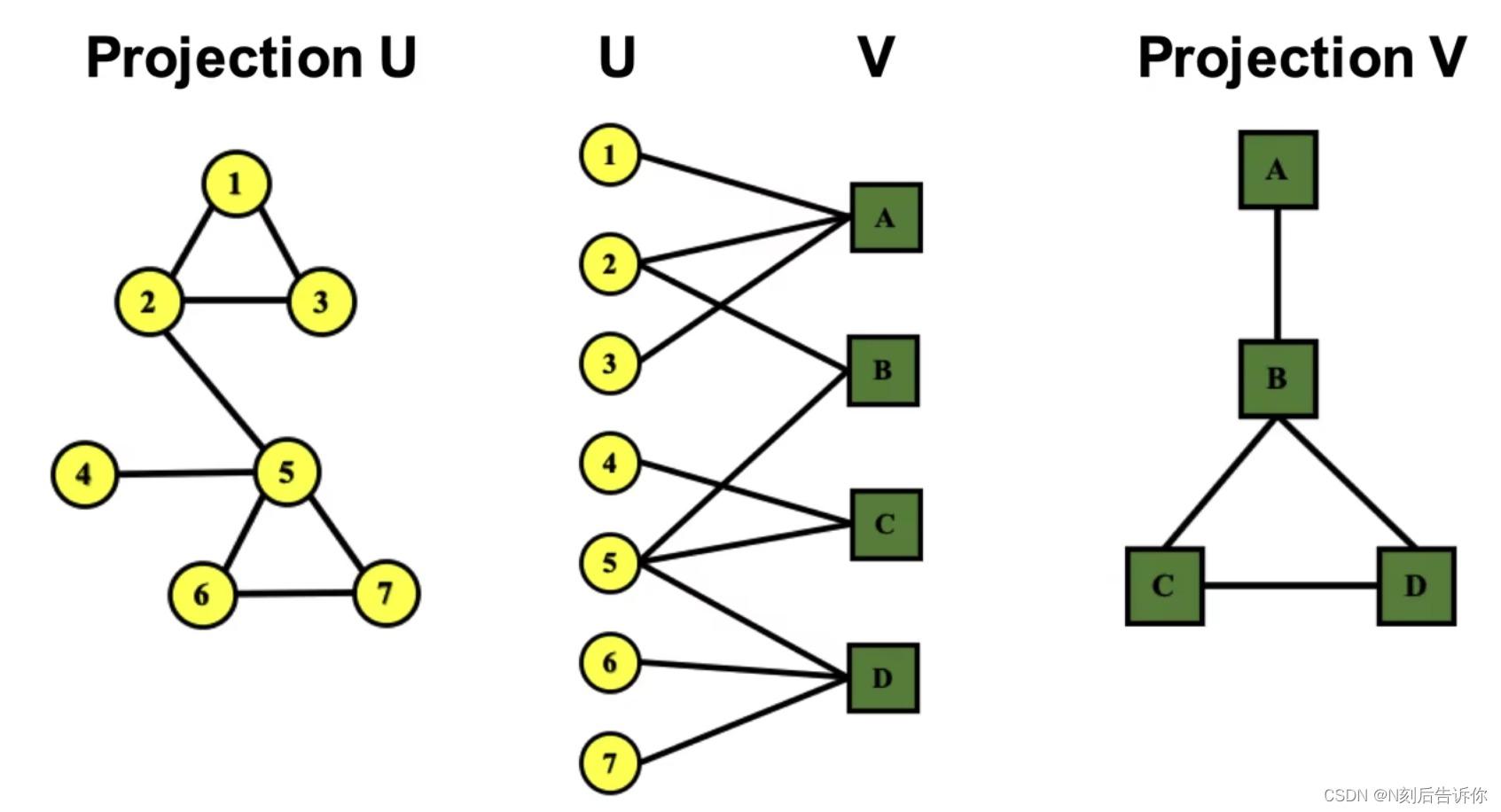
- 二分图(Bipartite Graph):节点种类是2的异质图被称为二分图。如论文作者和论文的关系、用户和商品之间的关系
二分图可以展开,如下图,在节点集U中,如果两个节点都连接到V中的同一个节点,则在图
Projection U中添加一条连接。
这样就可以将二分图转化为两张各自只有一类节点的图。
节点的度(Node degree)
-
对于无向图
-
- 第
i个节点的度:记为 k i k_i ki,表示与第i个节点邻接的边的数量
- 第
-
- 图的平均度: k ˉ = ⟨ k ⟩ = 1 N ∑ i = 1 N k i = 2 E N \bar{k}=\langle k\rangle=\frac{1}{N} \sum_{i=1}^N k_i=\frac{2 E}{N} kˉ=⟨k⟩=N1∑i=1Nki=N2E
-
对于有向图
-
- 入度:从别的节点指向当前节点的边的总数
-
- 出度:从当前节点指向别的节点的边的总数
-
- 节点的度=入度+出度
-
- 图的平均度: k ˉ = E N \bar{k}=\frac{E}{N} kˉ=NE
平均入度=平均出度,因为一个出度对应的边必然对应一个入度对应的边
入度为0的节点称为Source,出度为0的节点称为Sink
- 图的平均度: k ˉ = E N \bar{k}=\frac{E}{N} kˉ=NE
节点的度可以一定程度上反应节点的重要程度
图的基本表示-邻接矩阵
- 无向图
如果第i个节点和第j个节点之间存在边,则邻接矩阵A的 A i j A_{ij} Aij和 A j i A_{ji} Aji对应的值为1
无向图对应的邻接矩阵是对称阵
如果没有自身到自身的环,则主对角线全为0
- 有向图
如果第i个节点存在指向第j个节点之间的边,则邻接矩阵A的 A i j A_{ij} Aij对应的值为1
有向图对应的邻接矩阵是非对称阵
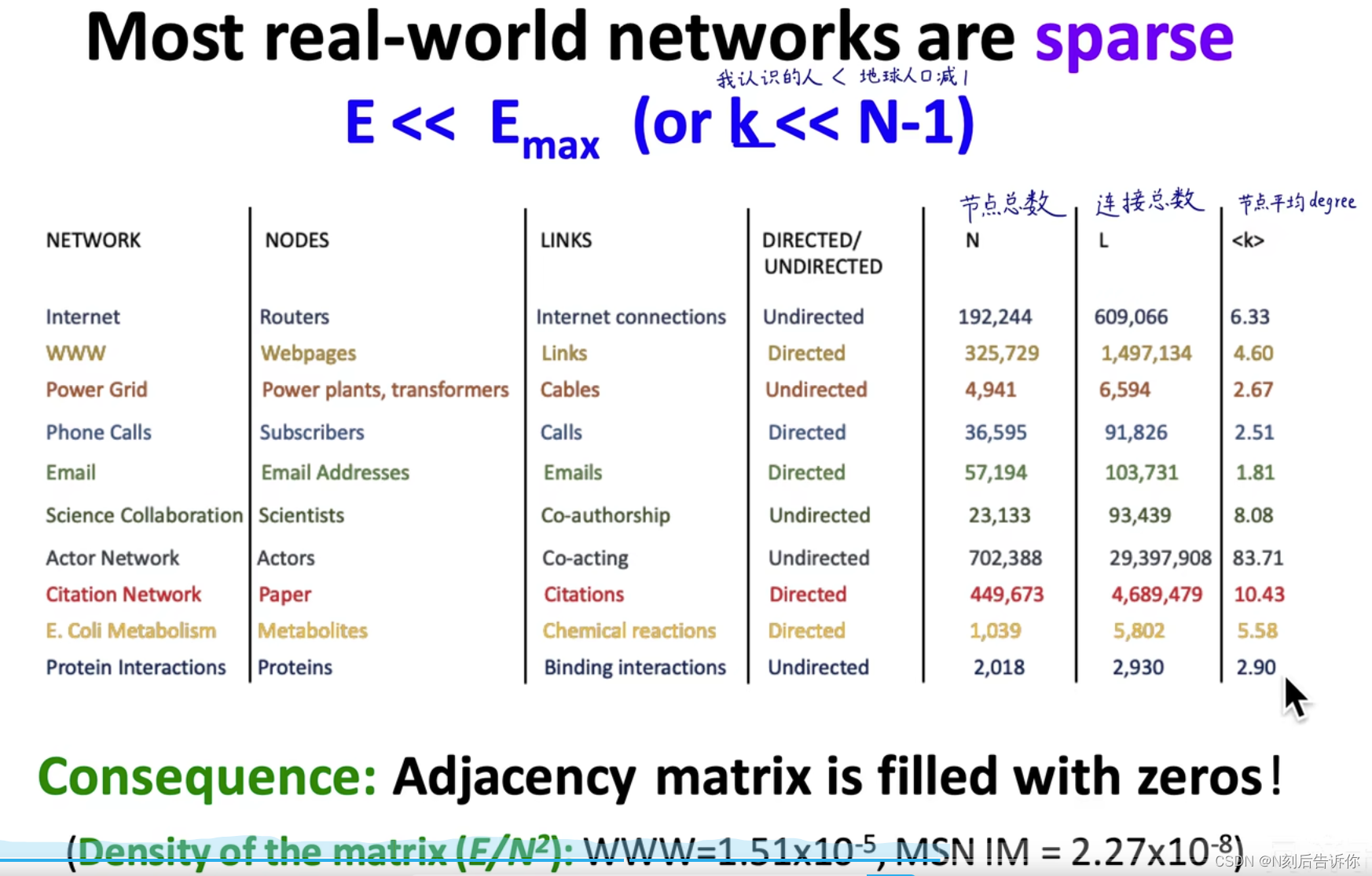
邻接矩阵是稀疏的,如社交网络
图的基本表示-连接列表和邻接列表
如上面所示,用邻接矩阵来表示图,存在稀疏性问题,造成存储空间的浪费。
- 连接列表:只记录存在连接的边和节点

- 邻接列表:对于一个给定节点,只记录他指向的节点和对应的边

上述图是无权图,在邻接矩阵中的值非1即0,如果是带权图,则可以在邻接矩阵中将1改成权重。
图的连通性
-
无向图中
连通图(Connected graph):任意两个点都有一条路径可达,则称为连通图。
不连通图虽然本身不连通,但是可以划分得到多个连通分支(connected components)。最大的连通分支被称为Giant Component
孤立的节点称为Isolated node。
不连通矩阵的邻接矩阵呈现出分块对角的形式
如果存在一个节点将不连通图的两个连通分支连接上了,那么它会打破分块对角形式 -
有向图中
强连通的有向图:如果任意两个节点存在有向路径可达,则称为强连通的有向图。
弱连通的有向图:如果忽略边的方向,即将它看成无向图,此时如果图是连通的,那么这个有向图称为弱连通的。对于有向图,可能整体不是强连通的,但其中的某个子图是强连通的,称为强连通分支(Strongly connected components(SCC))
E和G指向SCC,称为In-componet、D和F是由SCC出发的,称为Out-component。
传统图机器学习的特征工程-节点
-
总的思路
本节用传统机器学习方法,做特征工程,人工设计一些特征,把节点,边,全图特征编码成d维向量,再用该向量进行后续机器学习预测。 -
1.特征工程
抽取d个特征,编码为d维向量。本节只考虑连接特征,不考虑属性特征。节点自己的特征,称为属性特征(Attributes)
节点和图中其他节点的连接关系,称为连接特征。 -
2.训练一个机器学习模型
利用RF、SVM、NN等进行训练。 -
3.应用模型
给定一个新的节点/链接/图,获得图她的特征并做预测。
本节主要聚焦无向图,并针对节点、边、图层面做特征工程。
节点层面的特征工程
目标:区分节点在图中的结构和位置,可考虑的(连接)特征有:节点的度(Node degree)、节点的重要度(Node centrality)、聚类系数(Clustering coefficient)、子图模式(Graphlets)
聚合系数是指,与当前节点邻接的节点是否有联系。
Node degree
Node degree只考虑了邻接节点的数量,不能反应节点的质量
Node centrality
Node centrality考虑了节点在图中的重要度。有不同的方式来对此进行建模:
-
特征向量重要度(Eigenvector centrality)
思想:如果一个节点的邻接节点很重要,那么这个节点也很重要
建模:
c v = 1 λ ∑ u ∈ N ( v ) c u c_v=\frac{1}{\lambda}\sum_{u \in N(v)} c_u cv=λ1u∈N(v)∑cuλ \lambda λ是归一化系数,往往是A的最大特征值
实现:这是一个递归问题,如何解决?
上面公式等价于求解 λ c = A c \lambda \boldsymbol{c}=\boldsymbol{A c} λc=Ac可以发现, c \boldsymbol{c} c向量就是 A \boldsymbol{A} A的最大特征值对应的特征向量
根据perron-frobenius定理,最大特征值 λ m a x \lambda_{max} λmax一定为正且唯一 -
Betweenness centrality
思想:如果在任意两个节点间的最短路径中,有一个节点频繁出现,那么这个节点可以被认为是重要的
建模:
c v = ∑ s ≠ v ≠ t # ( shortest paths betwen s and t that contain v ) # ( shortest paths between s and t ) c_v=\sum_{s \neq v \neq t} \frac{\#(\text { shortest paths betwen } s \text { and } t \text { that contain } v)}{\#(\text { shortest paths between } s \text { and } t)} cv=s=v=t∑#( shortest paths between s and t)#( shortest paths betwen s and t that contain v)

-
Closeness centrality
思想:如果一个节点到其他所有节点的路径都很短,那么这个节点可以被认为是重要的
建模:
c v = 1 ∑ u ≠ v shortest path length between u and v c_v=\frac{1}{\sum_{u \neq v} \text { shortest path length between } u \text { and } v} cv=∑u=v shortest path length between u and v1
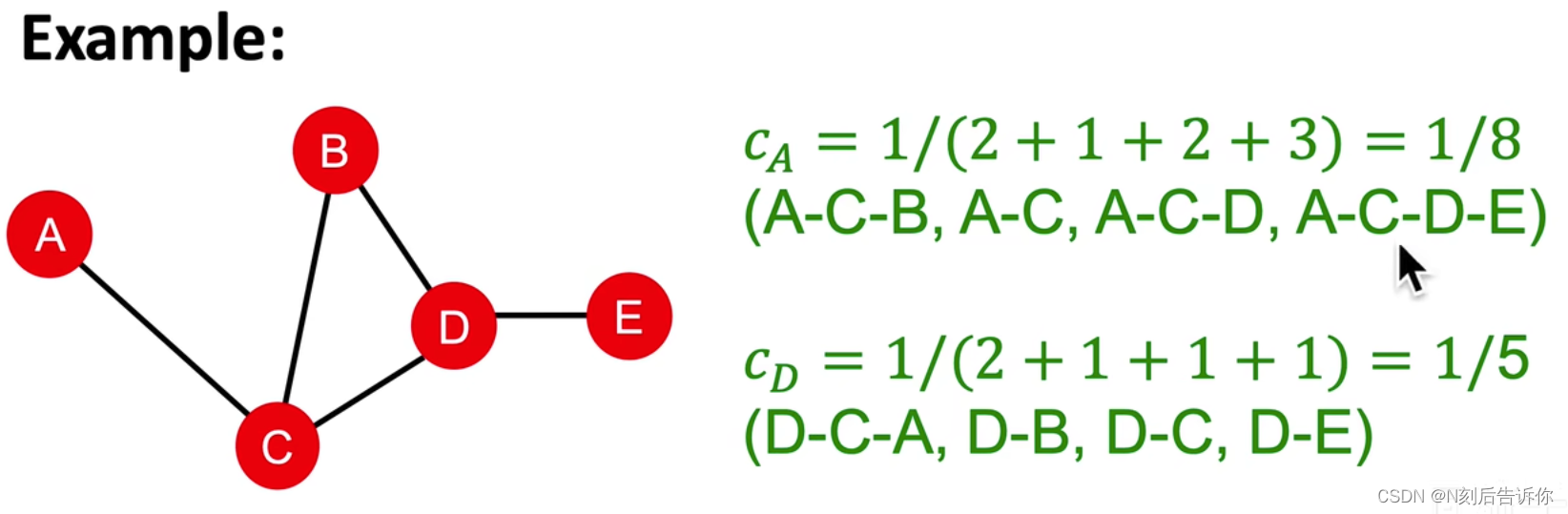
Clustering Coefficient
聚类系数(Clustering Coefficient),衡量一个节点的邻接节点的连接有多紧密。
建模:
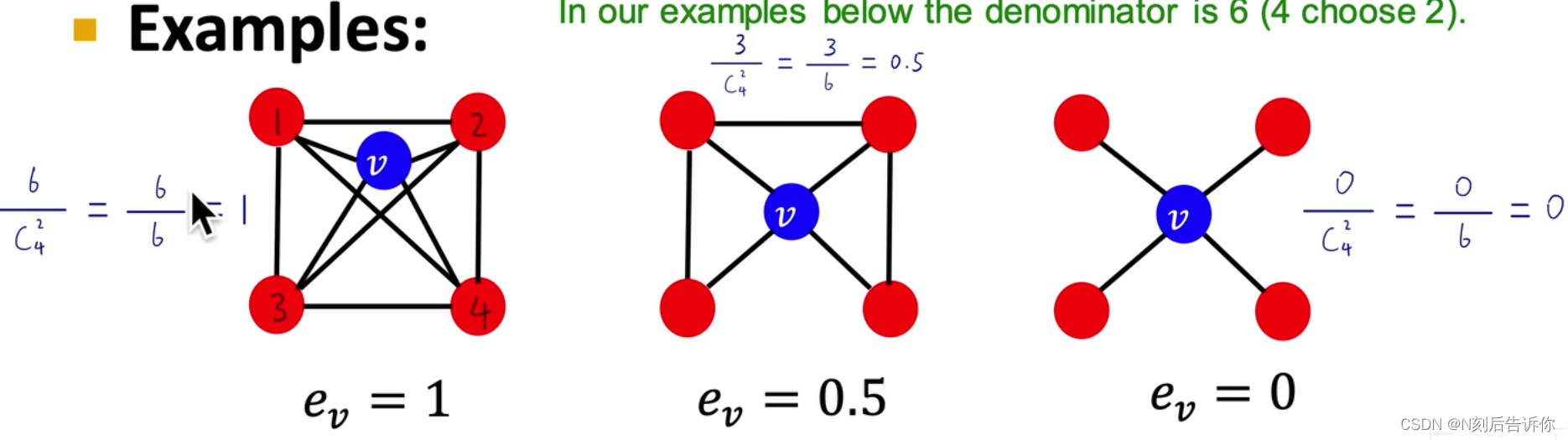
e v = # ( edges among neighboring nodes ) ( k v 2 ) ∈ [ 0 , 1 ] e_v=\frac{\#(\text{edges among neighboring nodes})}{\binom{k_v}{2}}\in [0, 1] ev=(2kv)#(edges among neighboring nodes)∈[0,1]
v节点相邻节点两两组成的节点对计入分母
如果节点对中的两个节点相邻,那么这对节点对计入分子
Graphlets
一个节点的自我网络(ego-network)是指以一个节点为中心,只包含他和他邻接节点,以及这些节点之间的边的图。
可以发现,节点v的聚类系数本质上就是计数了节点v的自我网络中以v为顶点的三角形的个数。
这个三角形可以理解为我们预先定义的一类子图。
那么如果修改这个预定义的子图类型,就可以得到新的计数特征,这个预定义的子图类型,就是我们下面要提到的graphlets。
先看看子图、生成子图、导出子图的概念:
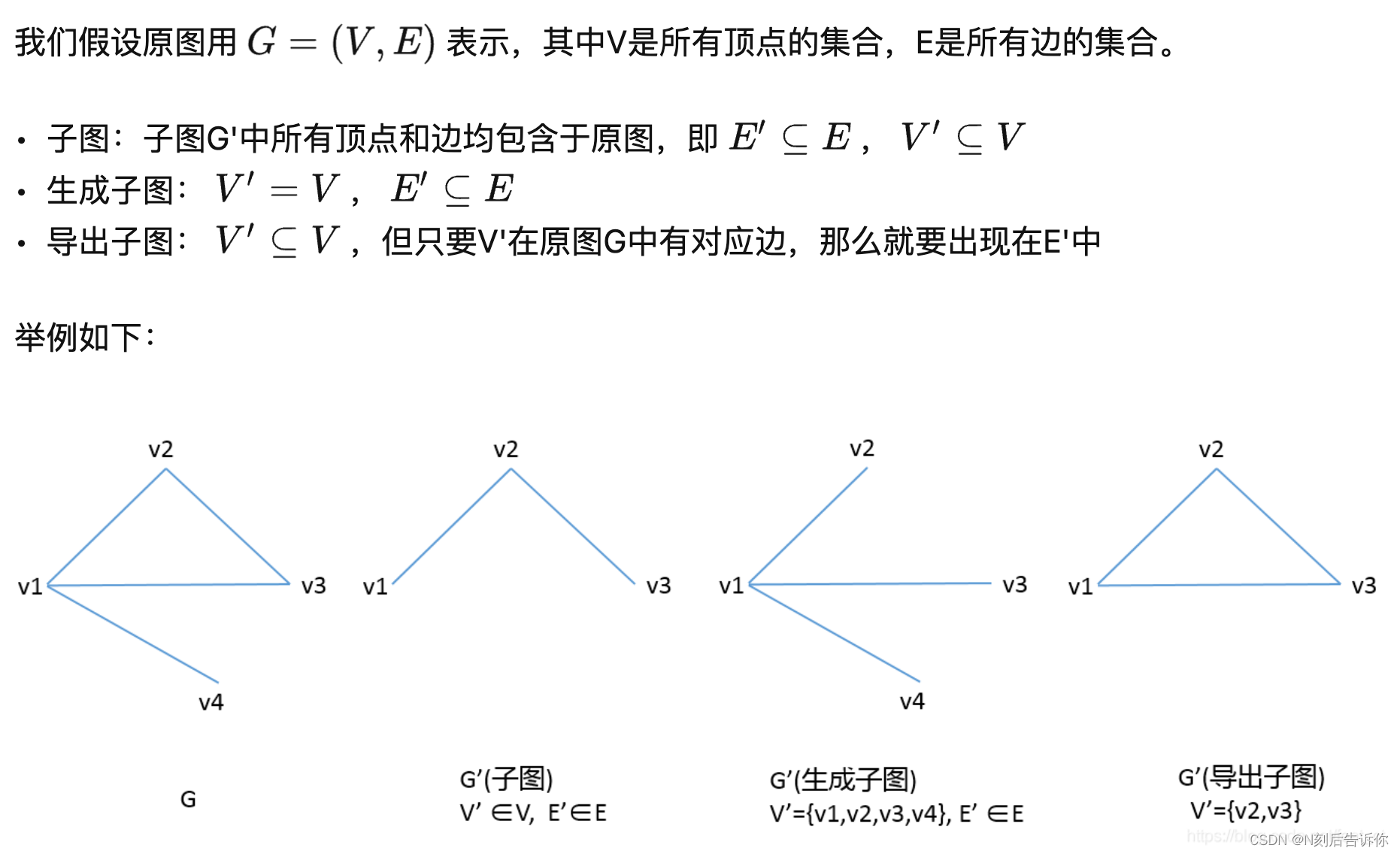
可以看到,从原图中取一些节点,并取这些节点所有出现的边可以构成导出子图。
下面给出Graphlets的精确定义,即有根连通导出异构子图(Rooted connected induced non-isomorphic subgraphs)
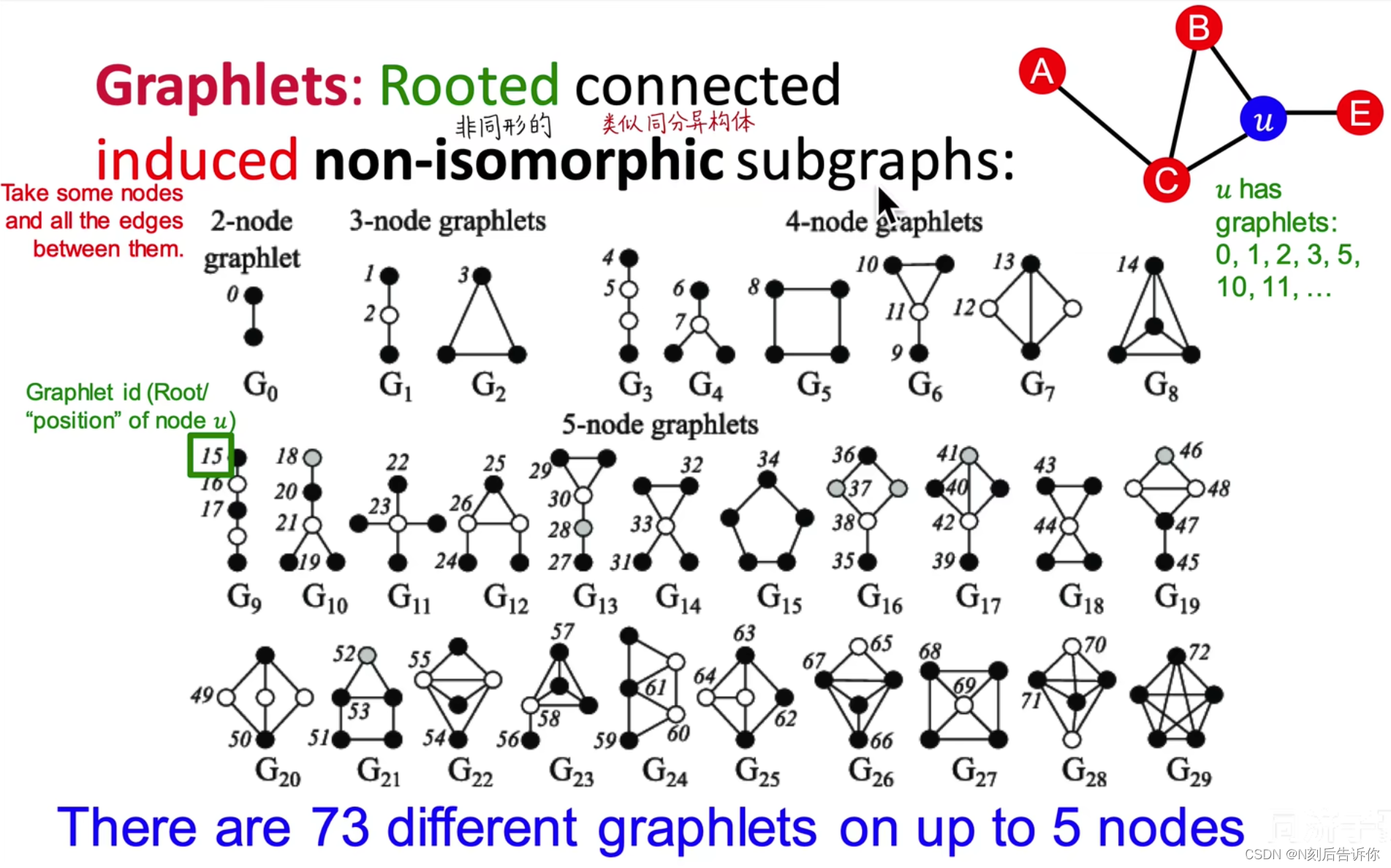
上图分别展示了2节点、3节点、4节点和5节点的graphlets,共有73种。
2个节点构成的子图中,可以定义1种类型的graphlet
3个节点构成的子图中,可以定义3种类型的graphlets
…
在右上角的例子中,节点u对应的graphlets类型有0、1、2、3、5、10、11、…
聚类系数中的三角形其实就是G2对应的graphlet。
下面引入Graphlets相关的特征向量:Graphlets Degree Vector(GDV),它一个基于给定节点,以它为根的各类graphlets的实例个数组成向量,如下面的例子。
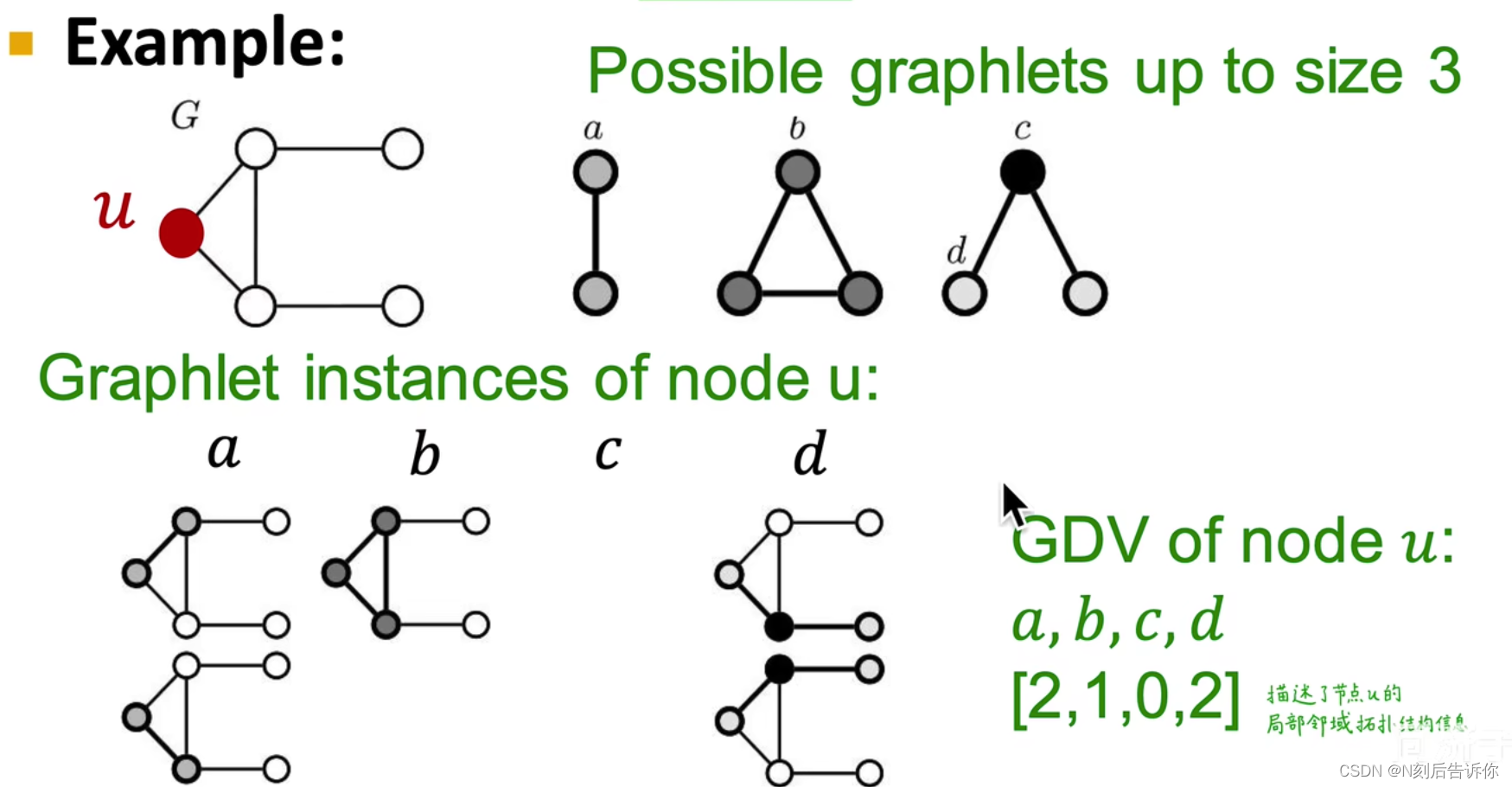
注意,原图中没有以c为根结点的导出子图。
GDV描述了节点局部领域的拓扑结构信息,用一些已经定义好的子图模式去匹配,并计数每种模式下的数量。
比较两个节点的GDV向量,可以计算距离和相似度。
在NetworkX中,子图模式Graphlets被称为Atlas
总结
介绍的结构特征可以分为:
基于重要度的特征(描述节点中心度/重要度):
- 节点的度
- 不同节点的重要度度量
可用于预测有影响力的节点
基于结构的特征(描述节点的邻域拓扑连接结构):
- 节点的度
- 聚类系数
- GDV
可用于预测节点在图中的功能,桥接、枢纽、中心
传统图机器学习的特征工程-连接
连接层面的预测任务:基于已知连接去预测(补全)未知连接。
在模型训练阶段,节点对被排序,top K节点对被预测。
关键是如何设计节点对的特征。
思路1:直接提取link的特征,变成d维向量。
思路2:把link两端的d维向量拼在一起,但是这会丢失link本身连接结构信息。
link prediction task有两种情况:
-
随机丢失连接:
对于客观静态图,如蛋白质,分子,我们可以通过随机移除一些连接,并尝试预测它们 -
随时间变化的连接:
对于如论文引用、社交网络、微信好友、学术合作等图,给定一段时间 [ t 0 , t 0 ′ ] [t_0, t_0^{'}] [t0,t0′]的图,预测下一个时间段 [ t 1 , t 1 ′ ] [t_1, t_1^{'}] [t1,t1′]的一个关于边的ranked list L。
评估的方式:先计算得到 [ t 1 , t 1 ′ ] [t_1, t_1^{'}] [t1,t1′]内真实出现的边的数量,记为 n = ∣ E n e w ∣ n=|E_{new}| n=∣Enew∣,然后从上面预测的列表中选出top n条边,然后计算预测的n个连接的准确率。
准确率 = 预测的 t o p n 个连接中正确的数量 n 准确率 = \frac{预测的top\ n个连接中正确的数量}{n} 准确率=n预测的top n个连接中正确的数量
连接层面的特征
连接的特征可以分为三类:基于距离的特征、基于两节点局部邻域信息的特征、基于两节点全局领域信息的特征
两节点的最短路径长度
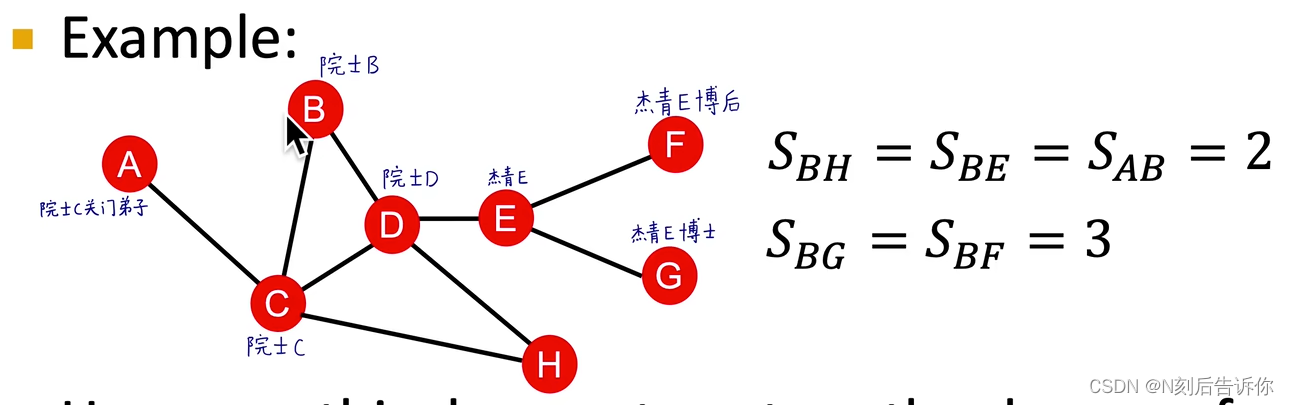
但仅考虑最短路径长度,会忽略连接的质量。如同样最短路径长度是2,A和B只有一条通路,而B和H有两条。
基于两节点局部邻域的信息
考虑两个节点v1和v2的邻接节点。
-
Common neighbors:
思路:记录共同好友个数
公式:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ \left|N\left(v_1\right) \cap N\left(v_2\right)\right| ∣N(v1)∩N(v2)∣ -
Jaccard’s coefficient:
思路:共同好友个数/两节点邻接节点的并集
公式:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ ∣ N ( v 1 ) ∪ N ( v 2 ) ∣ \frac{\left|N\left(v_1\right) \cap N\left(v_2\right)\right|}{\left|N\left(v_1\right) \cup N\left(v_2\right)\right|} ∣N(v1)∪N(v2)∣∣N(v1)∩N(v2)∣ -
Adamic-Adar index:
思路:共同好友是不是社牛,如果v1和v2的共同好友是社牛,那么v1和v2的联系就很廉价。
公式:
∑ u ∈ N ( v 1 ) ∩ N ( v 2 ) 1 log ( k u ) \sum_{u \in N\left(v_1\right) \cap N\left(v_2\right)} \frac{1}{\log \left(k_u\right)} u∈N(v1)∩N(v2)∑log(ku)1
基于两节点的局部邻域信息的特征的缺点是:对于没有共同好友的两节点,他们的上述度量都是0。
但事实上,他们在未来可能会有连接。
而全局领域的信息度量可以解决这个缺陷。
基于两节点全局领域的信息
Katz index:
思路:计数节点u和v之间所有长度路径的加权和
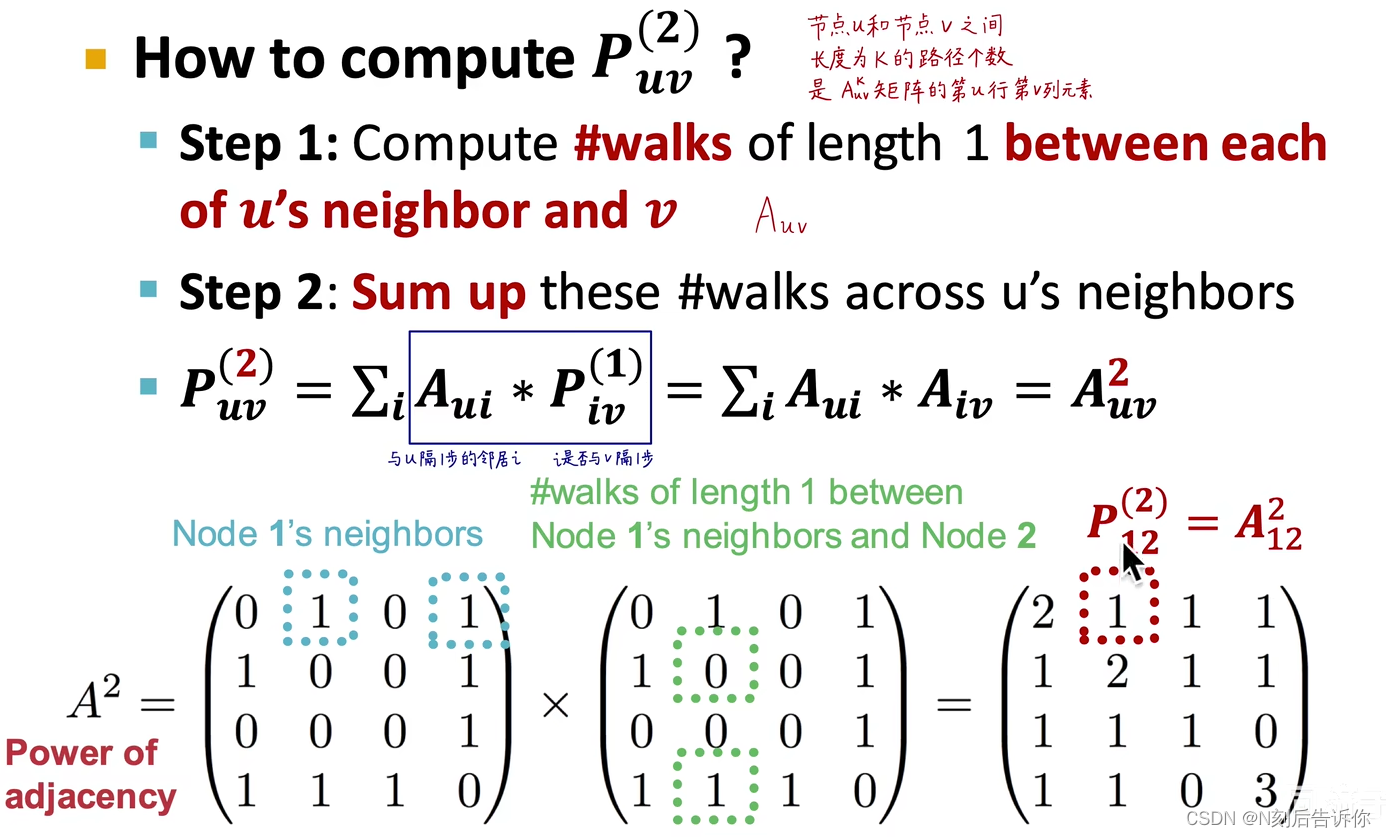
可以使用图邻接矩阵的幂可以结算长度为k的路径个数
结合下图,利用数学归纳法,可以推导出 A u v l A_{u v}^l Auvl表示节点u和v之间长度为l的路径个数。
公式:
S v 1 v 2 = ∑ l = 1 ∞ β l A v 1 v 2 l S_{v_1 v_2}=\sum_{l=1}^{\infty} \beta^{l} A_{v_1 v_2}^l Sv1v2=l=1∑∞βlAv1v2l
其中, 0 < β < 1 0<\beta<1 0<β<1表示折减系数
它的等价矩阵形式是(类比等比数列求和,并求无穷级数可得):
( I − β A ) − 1 − I (\boldsymbol{I}-\beta \boldsymbol{A})^{-1}-\boldsymbol{I} (I−βA)−1−I
一般可以将最大特征值的倒数作为折减系数 β \beta β
传统图机器学习的特征工程-全图
目标:将全图 G G G的结构特点表示为一个d维特征向量 ϕ ( G ) \phi(G) ϕ(G)。
Bag-of-*
思路:类比NLP中的Bag-of-Words,
Bag-of-nodes.
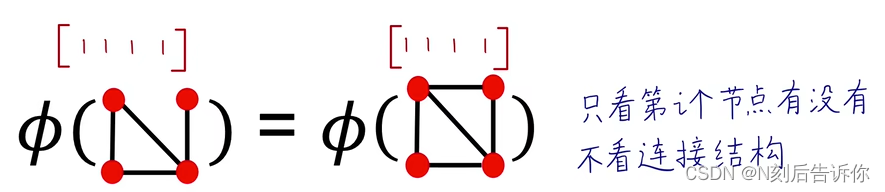
Bag-of-node degrees
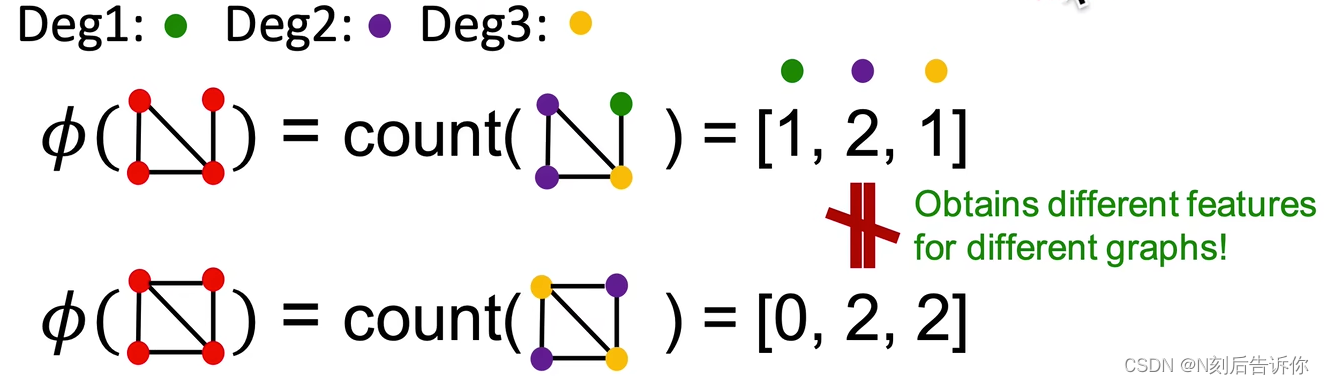
Bag-of-graphlets
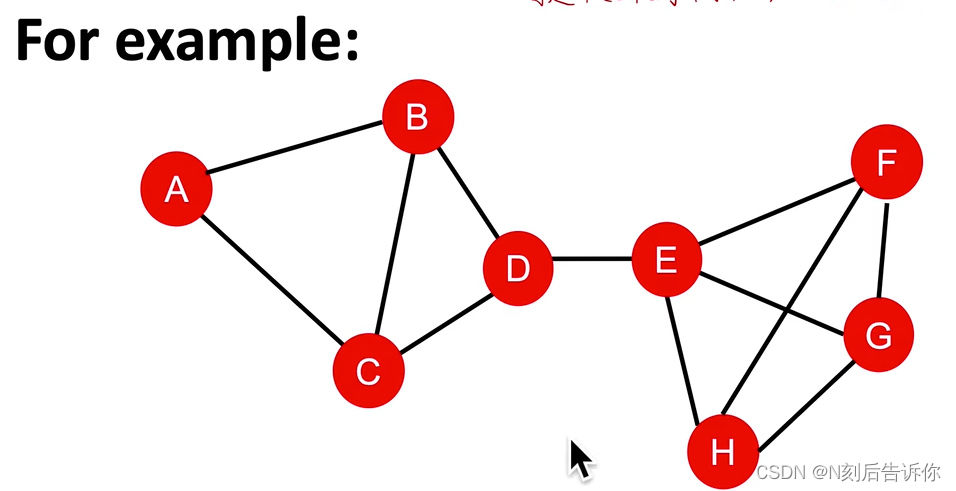
注意,这里是从全图的视角去分析,所以这里的graphlets和前面在节点特征工程中提到的graphlets有两点不同:
可以存在孤立节点的graphlets
graphlets不区分根,如下图,g2对应一个graphlets,而不是两个(如果考虑根,是两个)
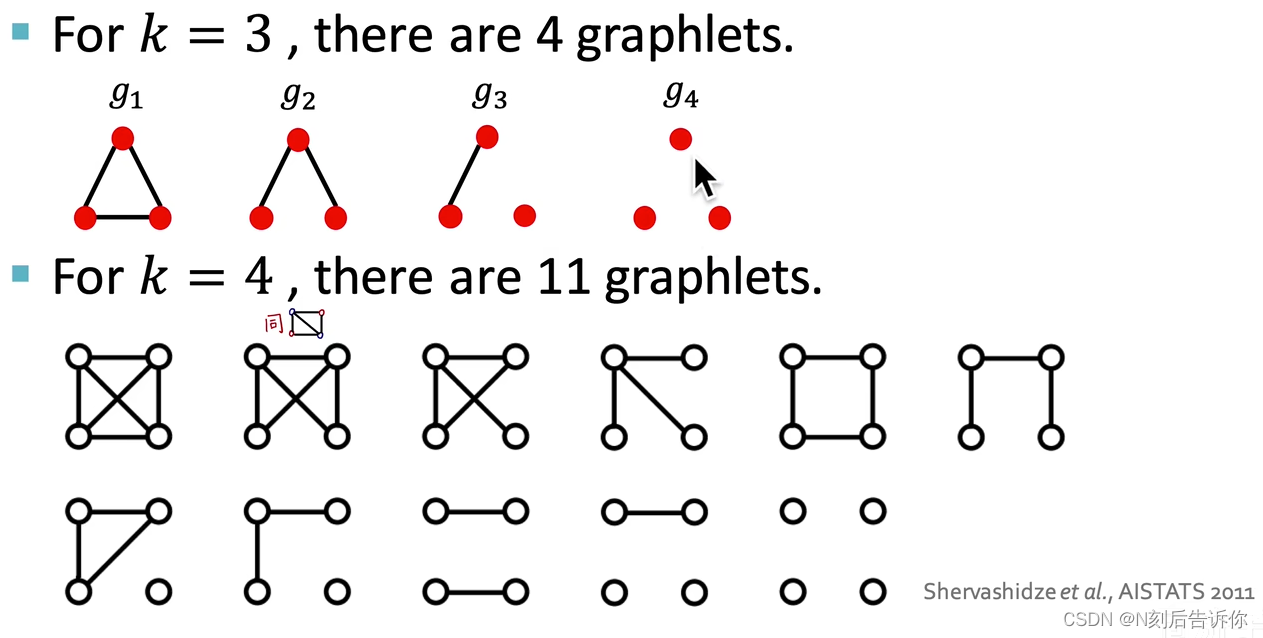
Graphlet Count Vector:给定一个图G,和graphlets列表 G k = ( g 1 , g 2 , . . . g n k ) G_k=(g_1,g_2, ... g_{n_k}) Gk=(g1,g2,...gnk),Graphlet Count Vector可以定义为(向量的第i个分量可以定义为第i个graphlet在全图中的个数):
( f G ) i = # ( g i ⊆ G ) for i = 1 , 2 , … , n k \left(f_G\right)_i=\#\left(g_i \subseteq G\right) \text { for } i=1,2, \ldots, n_k (fG)i=#(gi⊆G) for i=1,2,…,nk
例子:
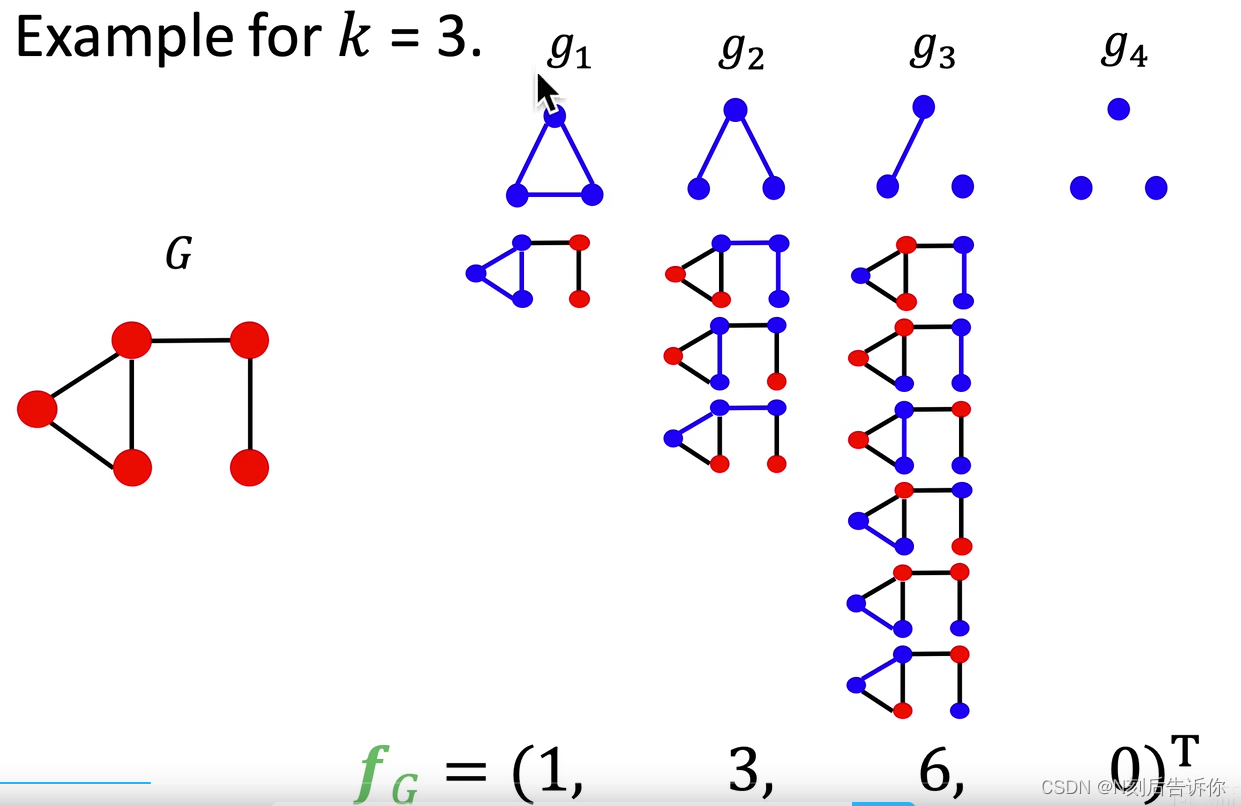
给定两个图, G G G和 G ′ G' G′,且有了它们对应的GCV,进一步,可以计算Graphlet Kernel:
K ( G , G ′ ) = f G T f G ′ K\left(G, G^{\prime}\right)=\boldsymbol{f}_G^{\mathrm{T}} \boldsymbol{f}_{G^{\prime}} K(G,G′)=fGTfG′
它可以反应这两张图的关系。
如果两个GCV的数量级悬殊,那么则需要先对这两个特征向量作归一化: h G = f G Sum ( f G ) \boldsymbol{h}_G=\frac{\boldsymbol{f}_G}{\operatorname{Sum}\left(\boldsymbol{f}_G\right)} hG=Sum(fG)fG,再计算Graphlet Kernel: K ( G , G ′ ) = h G T h G ′ K\left(G, G^{\prime}\right)=\boldsymbol{h}_G{ }^{\mathrm{T}} \boldsymbol{h}_{G^{\prime}} K(G,G′)=hGThG′
获取GCV在算力上是很昂贵的,在大小为n的图上对大小为k的graphlet作子图匹配,需要的时间复杂度是多项式复杂度: O ( n k ) O(n^k) O(nk)。
即使图节点的度被限制为 d d d,复杂度也仍有 O ( n d k − 1 ) O(nd^{k-1}) O(ndk−1)
Weisfeiler-Lehman Kernel
由于Graphlets Kernel不够高效,下面引入更高效的Weisfeiler-Lehman Kernel。
目标:设计一个更高效的特征编码。
思路:使用邻域结构迭代式地丰富节点词库
算法实现:颜色微调
主要的步骤是:
- 1.初始化颜色
- 2.聚合邻域的颜色+对聚合后的颜色进行哈希映射:
c ( k + 1 ) ( v ) = HASH ( { c ( k ) ( v ) , { c ( k ) ( u ) } u ∈ N ( v ) } ) c^{(k+1)}(v)=\operatorname{HASH}\left(\left\{c^{(k)}(v),\left\{c^{(k)}(u)\right\}_{u \in N(v)}\right\}\right) c(k+1)(v)=HASH({c(k)(v),{c(k)(u)}u∈N(v)})
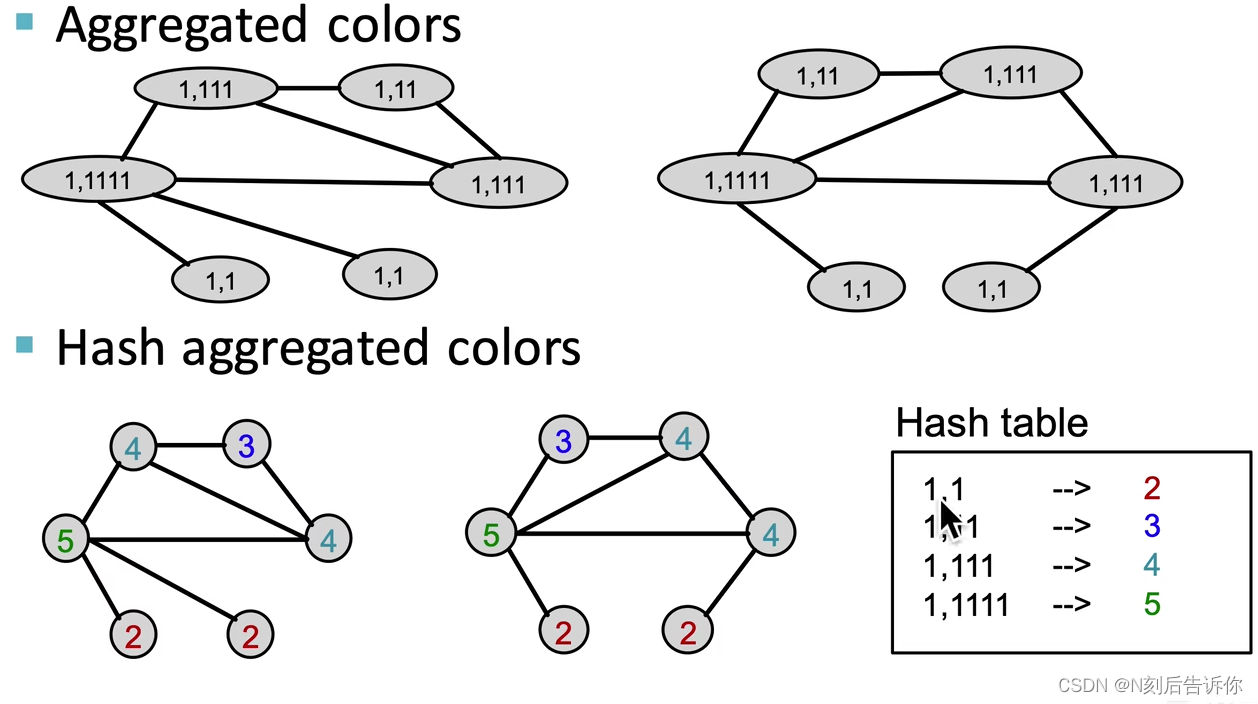
哈希表由两张图共同贡献
- 3.重复执行k次2的操作,获得 c ( K ) ( v ) c^{(K)}(v) c(K)(v),根据所有出现过的颜色,统计次数,得到 ϕ ( G ) \phi(G) ϕ(G)
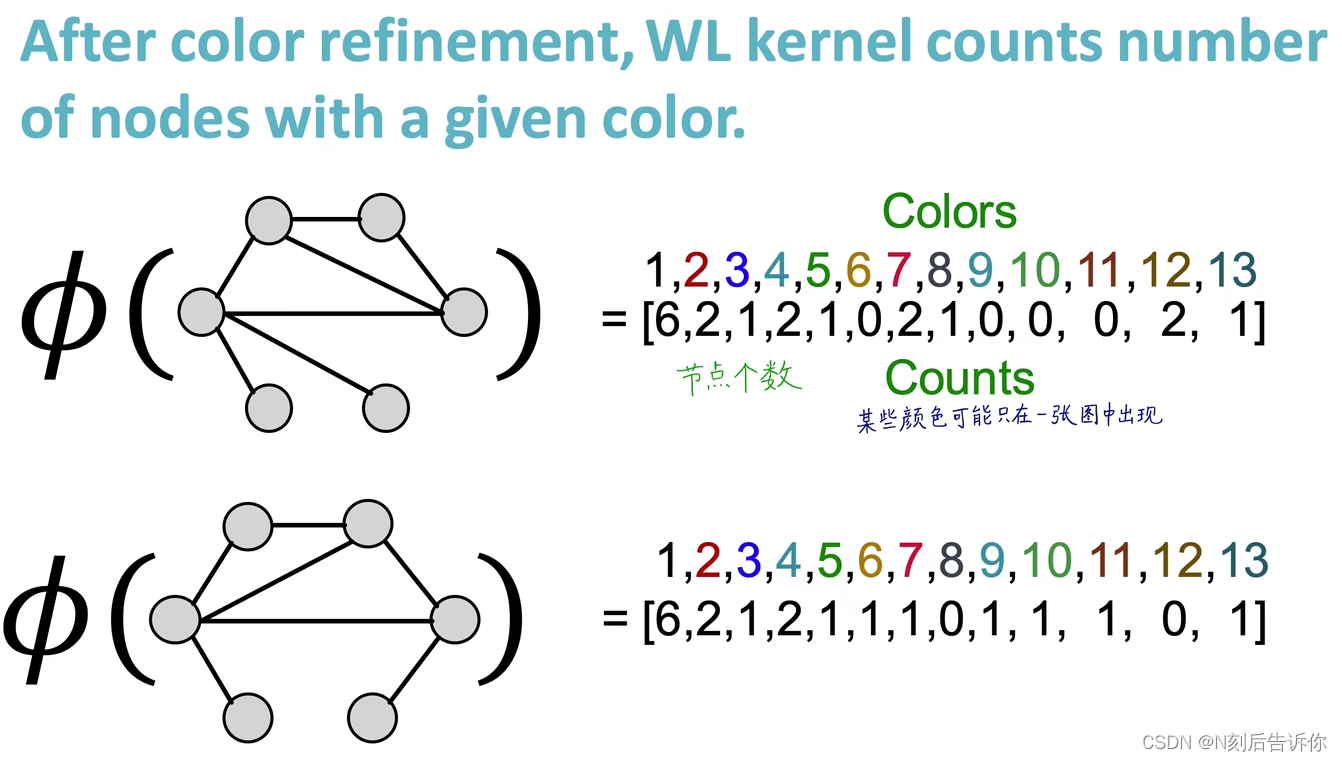
c ( K ) ( v ) c^{(K)}(v) c(K)(v)中包含了K跳邻域的信息。
- 4.计算WL Kernel: ϕ ( G ) T ϕ ( G ) \phi(G)^T\phi(G) ϕ(G)Tϕ(G)
总体而言,WL Kernel的时间复杂度是O(#(edges))。
kernel methods
核方法是传统技巧学习在图层面的预测的常用方法。它的核心是如何设计Kernel而非特征向量。
Kernel K ( G , G ′ ) K(G, G') K(G,G′)是标量,描述了数据间的相似度
核矩阵 K = ( K ( G , G ′ ) ) G , G ′ \boldsymbol{K}=\left(K\left(G, G^{\prime}\right)\right)_{G, G^{\prime}} K=(K(G,G′))G,G′永远半正定,即有正的特征值。
存在特征表示 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)使得 K ( G , G ′ ) = ϕ ( G ) T ϕ ( G ′ ) K\left(G, G^{\prime}\right)=\phi(G)^{\mathrm{T}} \phi\left(G^{\prime}\right) K(G,G′)=ϕ(G)Tϕ(G′)
一定kernel确定了,现成的机器学习模型,如Kernel SVM就可以用来预测。
Node Embeddings-图嵌入表示学习
图表示学习减轻了做特征工程的工作。
映射得到的向量具有低维(向量维度远小于节点数)、连续(每个元素都是实数)、稠密(每个元素都不为0)的特点。
图嵌入-基本框架:编码器-解码器
假设:G是图,V是节点集,A是无权图,本节仍仅考虑连接信息,不考虑节点信息。
目标是:节点编码后,两节点在嵌入空间中的向量的(余弦)相似度可以反应(近似)两节点在图中的相似度。即
s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v)\approx \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u similarity(u,v)≈zvTzu
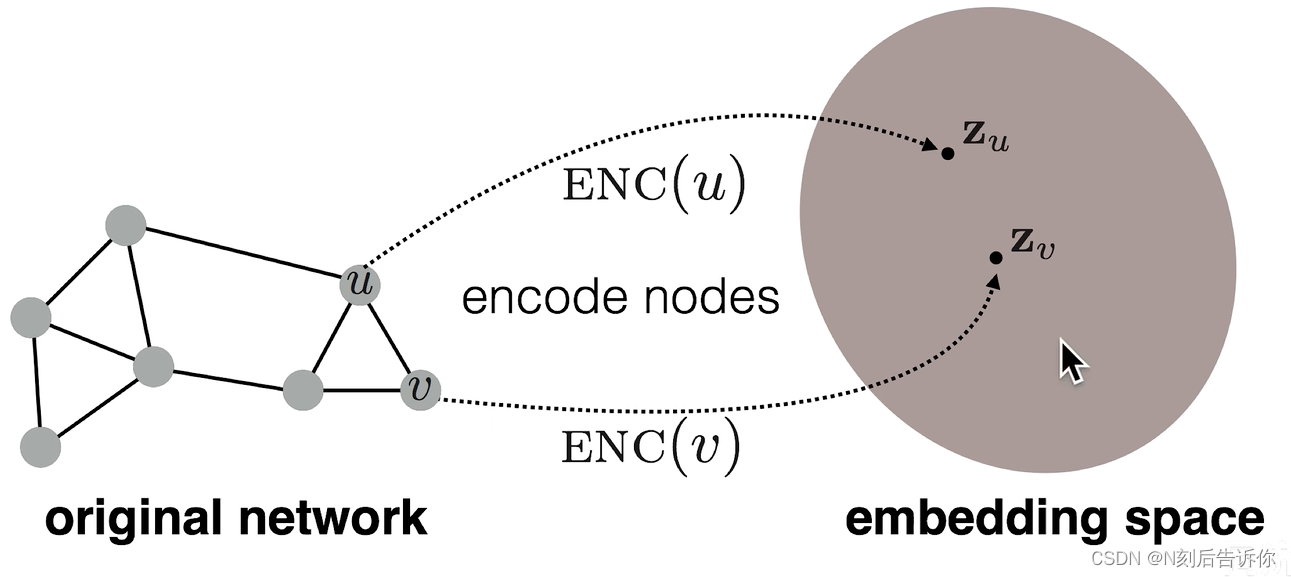
关键:如何定义节点的相似度。
步骤:
- 编码器:节点-》d维向量
- 定义节点在图中的相似度函数: s i m i l a r i t y ( u , v ) similarity(u,v) similarity(u,v)
- 解码器:计算两个节点向量的相似度:如 z v T z u \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u zvTzu
- 迭代优化编码器的参数使得图中相似节点的向量数量积大,不相似节点向量数量积小: s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v)\approx \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u similarity(u,v)≈zvTzu
node embeddings方法是无监督/自监督的,且与下游任务无关。
浅编码器
最简单的编码器-查表
只需要直接优化Z矩阵
对应方法有:DeepWalk,node2vec

基于随机游走的方法
图机器学习的很多概念可以类比NLP的很多概念
[暂时跳过这里去看DeepWalk论文精读]