139. 单词拆分
链接: 139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
1.状态表示*
这⾥我们选择⽐较常⽤的⽅式,以某个位置为结尾,结合题⽬要求,定义⼀个状态表⽰:
dp[i] 表⽰: [0, i] 区间内的字符串,能否被字典中的单词拼接⽽成
2.状态转移方程
对于 dp[i] ,为了确定当前的字符串能否由字典⾥⾯的单词构成,根据最后⼀个单词的起始位1置 j ,我们可以将其分解为前后两部分:
- i. 前⾯⼀部分 [0, j - 1] 区间的字符串;
- ii. 后⾯⼀部分 [j, i] 区间的字符串。
其中前⾯部分我们可以在 dp[j - 1] 中找到答案,后⾯部分的⼦串可以在字典⾥⾯找到。
因此,我们得出⼀个结论:当我们在从 0 ~ i 枚举 j 的时候,只要 dp[j - 1] = true
并且后⾯部分的⼦串 s.substr(j, i - j + 1) 能够在字典中找到,那么 dp[i] =true 。
3. 初始化
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:
i. 辅助结点⾥⾯的值要「保证后续填表是正确的」;
ii. 「下标的映射关系」;
在本题中,最前⾯加上⼀个格⼦,并且让 dp[0] = true ,可以理解为空串能够拼接⽽成。其中为了⽅便处理下标的映射关系,我们可以将字符串前⾯加上⼀个占位符 s = ’ ’ + s ,这样就没有下标的映射关系的问题了,同时还能处理「空串」的情况。
4. 填表顺序
显⽽易⻅,填表顺序「从左往右」
5. 返回值
根据状态表示,返回dp[n].
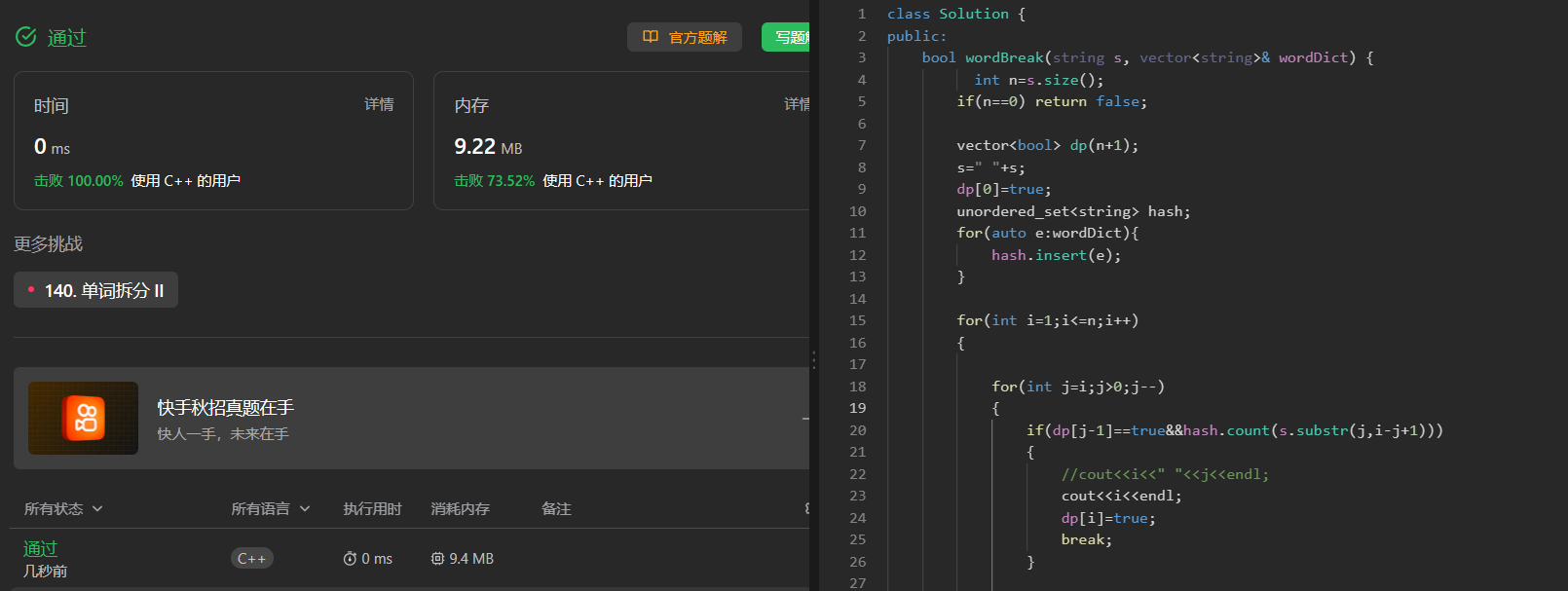
代码:
bool wordBreak(string s, vector<string>& wordDict) {int n=s.size();if(n==0) return false;vector<bool> dp(n+1);s=" "+s;dp[0]=true;unordered_set<string> hash;for(auto e:wordDict){hash.insert(e);}for(int i=1;i<=n;i++){for(int j=i;j>0;j--){if(dp[j-1]==true&&hash.count(s.substr(j,i-j+1))){//cout<<i<<" "<<j<<endl;cout<<i<<endl;dp[i]=true;break;}}//cout<<dp[i]<<endl;} return dp[n];}
467. 环绕字符串中唯一的子字符串
链接: 467. 环绕字符串中唯一的子字符串
定义字符串 base 为一个 “abcdefghijklmnopqrstuvwxyz” 无限环绕的字符串,所以 base 看起来是这样的:
“…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd…”.
给你一个字符串 s ,请你统计并返回 s 中有多少 不同非空子串 也在 base 中出现。
示例 1:
输入:s = “a”
输出:1
解释:字符串 s 的子字符串 “a” 在 base 中出现。
示例 2:
输入:s = “cac”
输出:2
解释:字符串 s 有两个子字符串 (“a”, “c”) 在 base 中出现。
示例 3:
输入:s = “zab”
输出:6
解释:字符串 s 有六个子字符串 (“z”, “a”, “b”, “za”, “ab”, and “zab”) 在 base 中出现。
1.状态表示*
dp[i] 表⽰:以 i 位置的元素为结尾的所有⼦串⾥⾯,有多少个在 base 中出现过。
2.状态转移方程
对于 dp[i] ,我们可以根据⼦串的「⻓度」划分为两类:
-
i. ⼦串的⻓度等于 1 :此时这⼀个字符会出现在 base 中;
-
. ⼦串的⻓度⼤于 1 :如果 i 位置的字符和 i - 1 位置上的字符组合后,出现在 base中的话,那么 dp[i - 1]
⾥⾯的所有⼦串后⾯填上⼀个 s[i] 依旧在 base 中出 现。因此 dp[i] = dp[i - 1] 。
综上, dp[i] = 1 + dp[i - 1] ,其中 dp[i - 1] 是否加上需要先做⼀下判断。
3. 初始化
可以根据「实际情况」,将表⾥⾯的值都初始化为 1 。
4. 填表顺序
显⽽易⻅,填表顺序「从左往右」
5. 返回值
⾥不能直接返回 dp 表⾥⾯的和,因为会有重复的结果。在返回之前,我们需要先「去重」:
- i. 相同字符结尾的 dp 值,我们仅需保留「最⼤」的即可,其余 dp 值对应的⼦串都可以在 最⼤的⾥⾯找到;
- ii. 可以创建⼀个⼤⼩为 26 的数组,统计所有字符结尾的最⼤ dp 值。
最后返回「数组中所有元素的和」即可。
代码:
int findSubstringInWraproundString(string s) {int n=s.size();vector<int> dp(n,1);for(int i=1;i<n;i++){//还需要去重if(s[i]==s[i-1]+1||(s[i]=='a'&&s[i-1]=='z'))dp[i]=dp[i-1]+1;}// 计算每⼀个字符结尾的最⻓连续⼦数组的⻓度int hash[26] = { 0 };for(int i = 0 ; i < n; i++)hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);// 3. 将结果累加起来int sum = 0;for(auto x : hash) sum += x;return sum;}