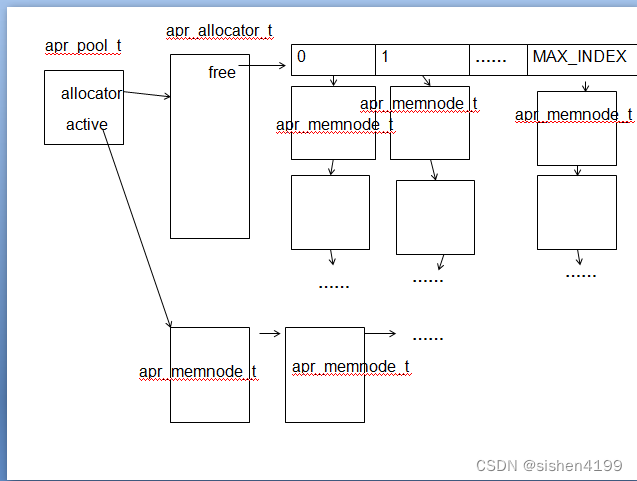
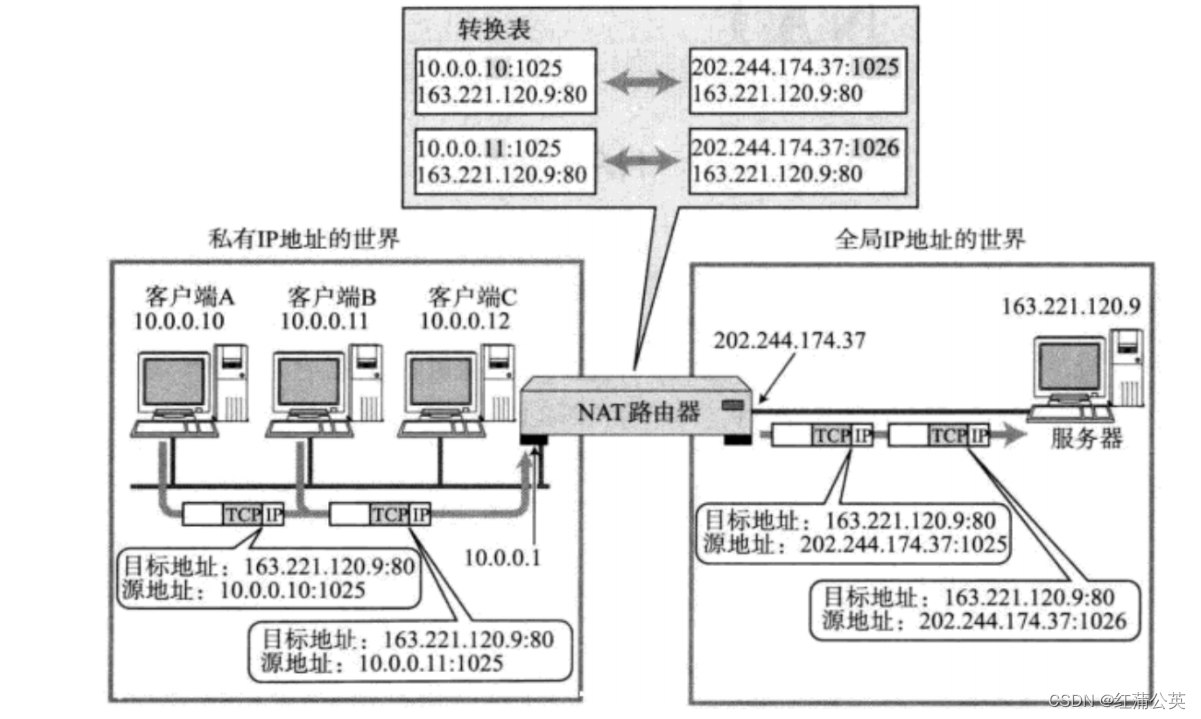
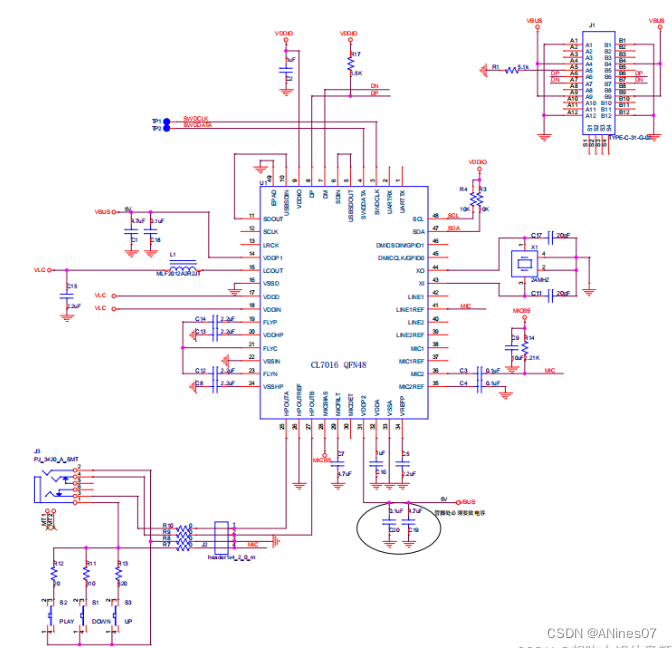
首先从散度的物理解释开始。首先，在球内的向量场的散度的积分，等于它在球边界上的流量的积分。所以根据积分中值定理，我们可以这么理解散度，它就是这个体积内的速度场的平均密度。而速度场只和源有关，所以它表示的某个点的源的密度。 

这里引出了狄拉克函数。因为存在一个点，它的密度是无穷大的。我们不好定义这样的函数，但我们可以定义它的积分。

 这里用了和散度一样的方法，不过分母不是体积，而是面积，这和普通的密度概念不太一样。但我们可以知道，它应该和旋转有关。在某个点的邻域的瞬时旋转轴，绕轴的瞬时角速度和旋转方向，就是旋度。

梯度比较简单，就不详细说了。

 这些老师都有单独证明，我们就不仔细说了。

这是在梯度散度旋度下的斯托克斯公司的写法。

 最后是格林公式。

 

 

 

后面因为不考虑具体的物理的例子的话，是很难有印象的。等后面需要用的时候再回来看吧。