一、什么是Numpy?

二、如何导入NumPy?

三、生成NumPy数组

3.1利用序列生成

3.2使用特定函数生成NumPy数组

（1）使用np.arange()

（2）使用np.linspace()

四、NumPy数组的其他常用函数

（1）np.zeros()

（2）np.ones()

五、N维数组的属性

1.NumPy数组的物理内存和逻辑视图

2.ndim属性

3.shape属性

六、NumPy数组中的运算

0.背景

1.数组向量运算

2.张量点乘运算

方法一：将二维数组转换为矩阵

方法二：使用张量点乘运算函数dot()

3.NumPy中提供的一些其他常用函数

参考：

说明：本文主要参考《Python极简讲义：一本书入门数据分析与机器学习》（2020年4月出版，电子工业出版社），本文图也是来源于这本书。

仅供学习使用。

R与Python系列第三篇，实际上内容全是Python的内容，跟R没有一点关系，只不过是本人学习Python的第三篇文章，想将R与Python结合使用。当在RStudio中配置好Python环境后（可以看R与Python系列第一篇），Python的代码可以在RStudio中运行，在RStudio的console中>>>表示此时运行的是Python代码，>表示运行R代码。

一、什么是Numpy?

在机器学习算法中，经常会用到数组和矩阵（向量）运算。NumPy是Python的基础，更是数据科学的通用语言，而且与TensorFlow关系密切。

为什么NumPy如此重要？实际上Python本身含有列表（list）和数组（array)，但对于大数据来说，这些结构有很多不足。

虽然Python中提供了列表，它可以当作数组使用。但是列表中的元素可以是任意“大杂烩”对象，因此为了区分彼此，列表付出了额外的代价----保存列表中每个对象的指针。这样一来，为了保存一个简单的列表，如[1,2,3,4]，Python就不得不配备四个指针，指向四个整数对象。也就是说是，Python不仅要保存对象1，2，3，4的内容，还要保存四个指针，增加了内存成本，是一种低效的行为。
Python中也提供了数组，但是它仅仅支持一维数组，不支持多维数组，也没有各种运算函数，因此不适合数值运算。
为了弥补Python数值计算的不足，Jim Hugunin、Travis Oliphant等人联合开发了NumPy项目，NumPy是Python语言的一个扩展程序库，是Numerical Python的简称，它提供了两种基本的对象： ndarray(N-dimensional array object)和ufunc(universal function object)。ndarray是存储单一数据类型的多维数组，而ufunc则是可以对数组进行处理的函数。NumPy支持多维度的数组（即N维数组对象ndarray）与矩阵运算，并对数组运算提供了大量的数学函数库。NumPy功能非常强大，支持广播、线性代数运算、傅里叶变换、随机数生成等功能，对很多第三方库（如SciPy、Pandas等）提供了底层支持。

二、如何导入NumPy?

NumPy是Python的外部库。由于Anaconda提供了“全家桶”式的服务，因此在安装Anaconda时，NumPy这个常用的第三方库也被默认安装了。但在使用时，NumPy还是需要显示导入的。使用外部库时，为了方便，我们常会为NumPy起一个别名，通常这个别名为np。

import numpy as np       #导入NumPy并制定别名
print(np.__version__)      #输出其版本号

我们可以使用np.__version__(注意：version前后都是两个下划线)输出NumPy的版本号，这句代码的附属目的是验证NumPy是否被正确加载。如果能正常显示版本号，则说明一切正常，我们可以开始如下的操作了。

三、生成NumPy数组

NumPy最重要的一个特点就是支持N维数组对象ndarray。ndarray对象与列表有相似之处，但也有显著区别。例如，构成列表的元素是大杂烩的，元素类型可以是字符串、字典、元组中的一种或多种，但是NumPy数组中的元素类型要求一致。

3.1利用序列生成

使用array()生成NumPy数组，array()可以接收任意数据类型（如列表、元组等）作为数据源。

如果构造NumPy数组的数据精度不一致，如有整数，也有浮点数，NumPy会自动把所有数据都转换为浮点数，这是因为浮点数的精度更高。

data1 <- [6, 8.5, 9, 0]
arr1 <- np.array(data1)
arr1
输出: array( [6., 8.5, 9., 0.] )

每个数组都有一个dtype属性，用来描述数组的数据类型。除非显示指定，否则np.array会自动推断数据类型。数据类型会被存储在一个特殊的元数据dtype中。

arr1.dtype                   #默认保存为双精度（64 bit）浮点数
输出：dtype('float64')

如果数据序列是嵌套的，且嵌套序列是等长的，则通过array()方法可以把嵌套的序列转为与嵌套级别适配的高维数组。

data2 = [ [1, 2, 3, 4], [5, 6, 7, 8] ]     #这是一个两层嵌套列表
arr2 = np.array(data2)                     #转换为一个二维数组
arr2输出：
array([[1, 2, 3, 4],[5, 6, 7, 8] ])

3.2使用特定函数生成NumPy数组

（1）使用np.arange()

arange(start, stop, step, dtype)

描述：arange()根据start与stop指定的范围及step设定的步长，生成一个ndarray对象，即一个数组，不仅可以直接输出，还可以当作向量，参与到实际运算当中。取值区间是左闭右开的，即stop这个终止值是不包括在内的。

start：起始值，默认为0；

stop：终止值；

step：步长，如果不指定，默认值为1；

dtype：指定返回ndarray的数据类型，如果没有提供，则会使用输入数据的类型。

arr3 = np.arange(10)     #生成0~9的ndarray数组
print(arr3)
输出：
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

ndarray对象可以做运算，如

arr3 = arr3 + 1      #将arr3中每个元素都加1
arr3
输出：
array( [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] )

需要说明的是，上述arr3是一个包含10个元素的向量[0,1,2,3,4,5,6,7,8,9]，它和标量“1”实施相加操作，原本在向量“尺寸”上是不适配的。之所以能成功实施，是因为利用了“广播”机制。广播机制将这个标量“1”扩展为等长的向量[1,1,1,1,1,1,1,1,1]，此时二者的维度是一样的，这才对两个长度不相等的向量进行了相加，这一点和R是一样的。

（2）使用np.linspace()

使用np.linspace()指定区间内生成指定个数的数组。（当然，也可以使用np.arange()，但是需要手动计算函数所需的步长）。

c = np.linspace(1, 10, 20)
c输出：
array([ 1.        ,  1.47368421,  1.94736842,  2.42105263,  2.89473684,3.36842105,  3.84210526,  4.31578947,  4.78947368,  5.26315789,5.73684211,  6.21052632,  6.68421053,  7.15789474,  7.63157895,8.10526316,  8.57894737,  9.05263158,  9.52631579, 10.        ])

上述代码使用np.linspace()在区间[1,10]中生成了20个等间隔的数据，该方法的前两个参数分别指明生成元素的左右区间边界，第三个参数确定上下限之间均匀等分的数据个数。

需要注意的是，np.arange()中数据区间是左闭右开的（即区间的最后一个数值是取不到的），而np.linspace()生成的数据区间是闭区间。当然可以指定np.linspace()中的参数endpoint=False，使生成数据区间编程左闭右开区间。

四、NumPy数组的其他常用函数

（1）np.zeros()

np.zeros()、np.ones()函数用来生成指定维数和填充固定数值的数组。其中，np.zeros()函数生成的数组由0来填充，np.ones()生成的数组由1来填充。它们通常用来对某些变量进行初始化。

>>> zeros = np.zeros((3,4))     #生成3X4的二维数组，元素均为0
>>> zeros
array([[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]])

值得注意的是，np.zeros((3,4))的含义。尺寸参数3和4使用两层括号包裹，实际上，应该将(3,4)整体看作是一个匿名元组对象，np.zeros((3,4))等价于np.zeros(shape=(3,4))，在shape参数处需要通过一个元组或者列表来指明生成数组的尺寸。

元组的外部轮廓是两个圆括号，那么在默认指定shape参数的情况下，那么在默认指定shape参数的情况下，这对圆括号就会和np.zeros()方法的外层括号相连，造成一定程度上的理解困扰，为此，推荐np.zeros( shape = [3,4] )，即将方括号作为轮廓特征的列表 来表示数组的尺寸。（元组的外部轮廓特征是两个圆括号，列表的外部轮廓特征是方括号。）

（2）np.ones()

类似地，可以用np.ones()生成指定尺寸、元素全为1的数组：

>>> ones_ = np.ones(shape = [3,4], dtype =float)
>>> ones_
array([[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]])

（3）.reshape() 重构数组尺寸

>>> arr = np.arange(6)         #创建一个一维数组，数组元素为0,1,...,5
>>> arr = arr.reshape((2,3))   #将arr的尺寸重构为两行三列
>>> arr
array([[0, 1, 2],[3, 4, 5]])

注意，reshape()内参数(2,3)的类型是元组，表示数组为两行三列的。

五、N维数组的属性

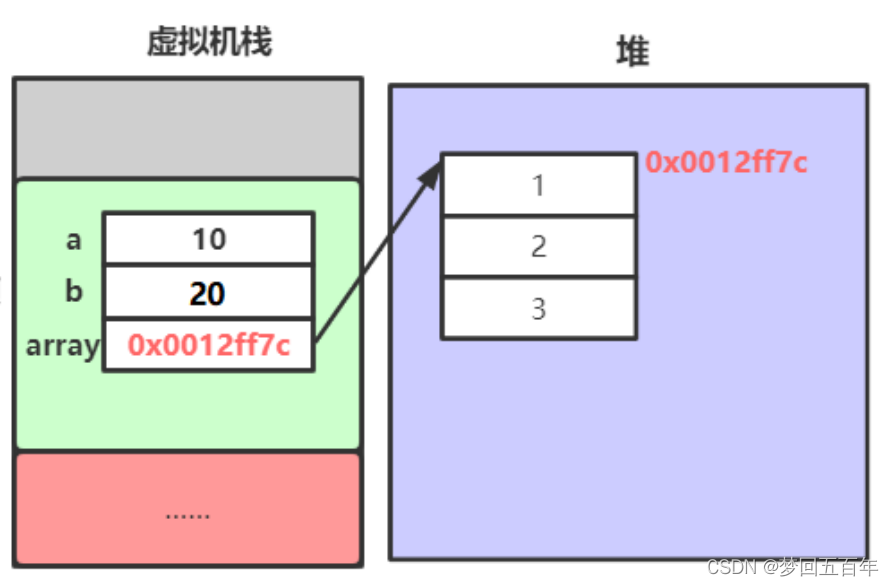
1.NumPy数组的物理内存和逻辑视图

需要说明的是，在物理内存中是不存在N维数组的，限于存储介质的物理特性，它永远只有一维结构。我们常见的便于理解的N维数组仅仅是“逻辑视图”，它们不过是包装出来的。NumPy数组的物理内存和逻辑视图如下图所示，“编译器”或第三方工具在幕后做了很多额外的工作，这才使得我们享受到了便利。（大致了解一下即可。）

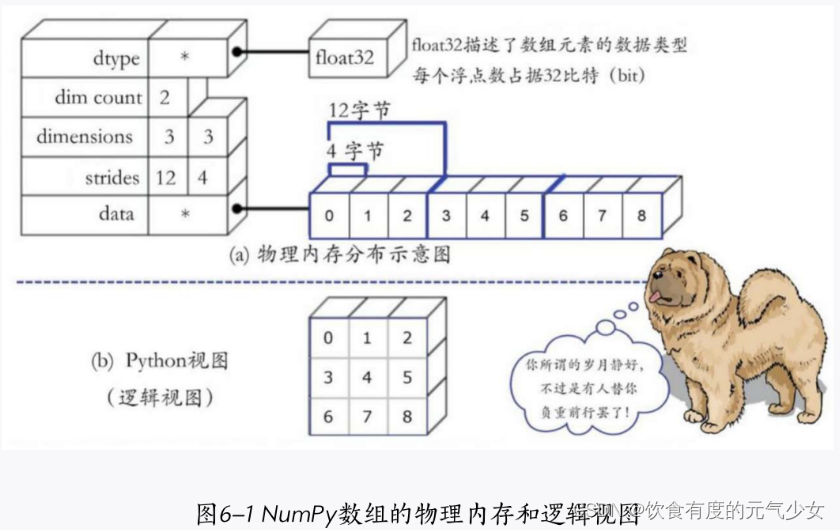
2.ndim属性

N维数组是包含同类型的数据容器，每个数组的维度（dimension）都是由一个ndim属性来描述。

使用.ndim来查看数组的维度。

一维数组，是由一个维度构成，.ndim=1, 有时候，一维数组也被称为1D张量（1D Tensor）。
二维数组，是由两个维度构成，.ndim=2，行和列，有时候，二维数组也被称为2D张量（2D Tensor）。
三维数组，是由三个维度构成，.ndim=3，通道、行和列（或者可以记为页，行，列，其中页表示书的一页，这只是为了便于记忆，没啥实质内容。）
以此类推。。。

>>> mp_array = np.arange(0,10)  #创建一个一维数组
>>> mp_array.ndim
1

3.shape属性

对于N维数组，shape（数组的形状）主要用来表示数组每个维度的数量，一维数组的shape就是它的长度。

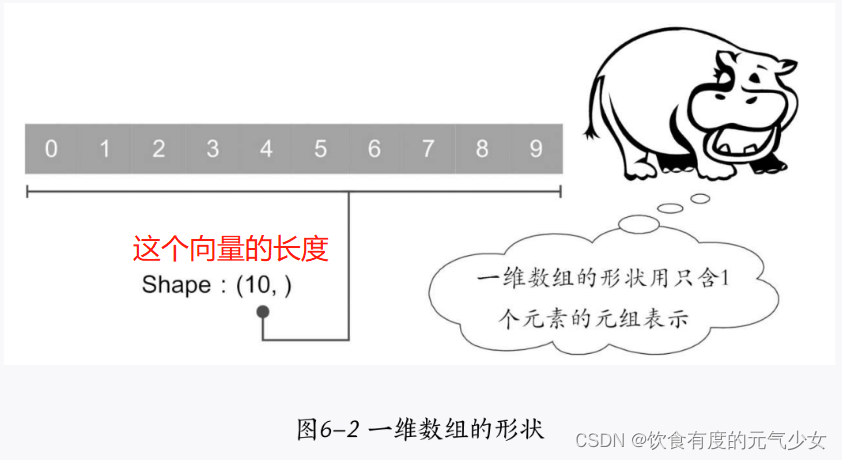
使用.shpae查看形状属性。

>>> mp_array.shape      #查看数组的形状信息
(10,)

NumPy数组形状并不是一成不变的，可以通过reshape()方法将原有数组进行“重构”（变形reshape）。

>>> b = np.arange(15)  #创建一个包含15个元素的一维数组
>>> b
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])
>>> b = b.reshape(3,5)  #改变数组形状为3行5列
>>> b
array([[ 0,  1,  2,  3,  4],[ 5,  6,  7,  8,  9],[10, 11, 12, 13, 14]])
>>> b.ndim  #查看数组的维度信息
2     #这是一个2D张量
>>> b.shape #查看数组的形状信息
(3, 5)
>>> b.size  #查看数组元素的总个数
15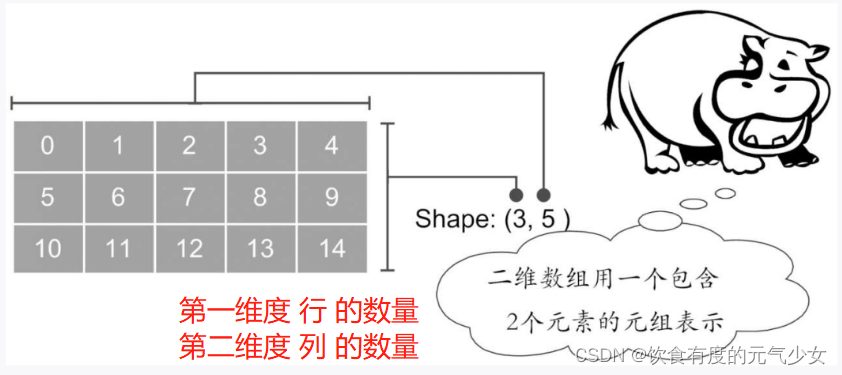

三维数组的构建

>>> a = np.arange(30).reshape(2,3,5) #重构数组为2通道3行5列
>>> a
array([[[ 0,  1,  2,  3,  4],[ 5,  6,  7,  8,  9],[10, 11, 12, 13, 14]],[[15, 16, 17, 18, 19],[20, 21, 22, 23, 24],[25, 26, 27, 28, 29]]])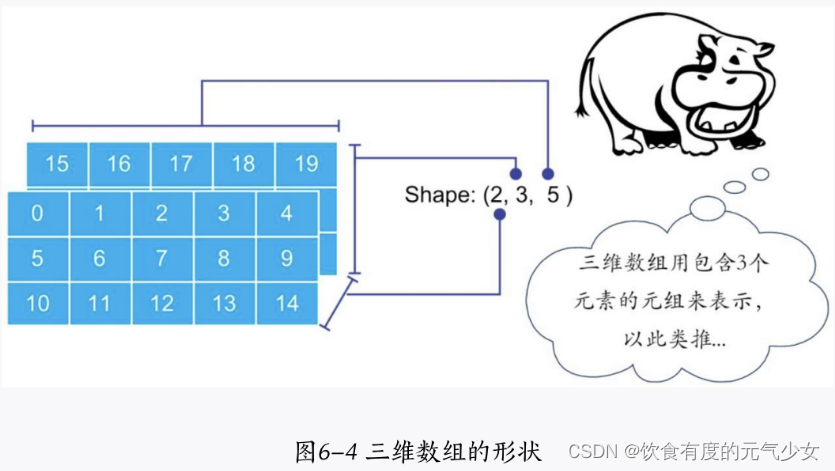

六、NumPy数组中的运算

0.背景

如果想要让两个列表对应元素相加，除了使用for循环，还可以使用列表推导式来完成这个任务（这里不介绍列表推导式，可以参考1中6.5.1内容。），列表不能直接进行对应元素的相加！而R中是可以直接进行向量化运算，即逐元素运算。

Python中由于NumPy扩展库使得数组可以进行向量化运算，NumPy扩展库是是一个久经考验的数值计算包，NumPy有十分成熟的算数运算函数，我们不需要给出复杂的计算公式，直接调用NumPy的内置函数，即可达到我们的运算目的。

列表是不能直接完成对应元素相加的，而NumPy数组是可以进行逐元素运算的，逐元素实施加、减、乘、除等运算。

事实上，NumPy中数组的运算，都是基于更为基础的算法库---基础线性子程序（basic linear algebra subprograms,简成BLAS）而实现的。BLAS是一个更底层的、高度并行和优化的张量操作程序，通常由Fortran、C语言编写。

1.数组向量运算

向量化运算即对应元素进行运算。要求两个对象的形状（即维数）是一样的。NumPy吸纳了Fortran或MATLAB等语言的优点，只要操作数组的形状（维度）一致，我们就可以很方便地对它们逐元素（element-wise）实施加、减、乘、除、取余、指数运算等操作。

>>> a = np.arange(10) #生成一维ndarray数组，长度为10
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b =np.linspace(1,10,10)#生成一维ndarray数组，长度为10
>>> b
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])
>>> a+b #数组加法
array([ 1.,  3.,  5.,  7.,  9., 11., 13., 15., 17., 19.])
>>> a-b #数组减法
array([-1., -1., -1., -1., -1., -1., -1., -1., -1., -1.])
>>> a*b #数组乘法
array([ 0.,  2.,  6., 12., 20., 30., 42., 56., 72., 90.])
>>> a/b#数组除法
array([0.        , 0.5       , 0.66666667, 0.75      , 0.8       ,0.83333333, 0.85714286, 0.875     , 0.88888889, 0.9       ])
>>> a%b #数组取余
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
>>> a**2 #数组元素平方
array([ 0,  1,  4,  9, 16, 25, 36, 49, 64, 81])

2.张量点乘运算

张量点乘运算是指二维数据在数学意义上的矩阵运算，点乘运算这个名称是由NumPy取的。

值得注意的是，二维数组和矩阵本质上是相同地，但是数组默认操作是基于“逐元素”原则的，所以要求两个操作对象之间的维度信息必须是一样的。然而，数学意义上的矩阵乘法不要求两个操作对象之间的维度是一样的，只要求前一个矩阵的列数等于后一个矩阵的行数。

如何执行矩阵的乘法运算？

方法一：将二维数组转换为矩阵；
方法二：使用张量点乘运算，是NumPy给矩阵乘法取得新名称dot（点乘）。

方法一：将二维数组转换为矩阵

>>> a = np.array([[1,2], [3,4]])
>>> a
array([[1, 2],[3, 4]])
>>> a = np.mat(a)  #将数组a转成矩阵a
>>> a
matrix([[1, 2],[3, 4]])>>> b = np.arange(8).reshape(2,4)
>>> b
array([[0, 1, 2, 3],[4, 5, 6, 7]])
>>> b = np.mat(b)  #将数组b转换成矩阵b
>>> b
matrix([[0, 1, 2, 3],[4, 5, 6, 7]])
>>> a*b #此时，矩阵a和矩阵b之间执行的是点乘运算
matrix([[ 8, 11, 14, 17],[16, 23, 30, 37]])

方法二：使用张量点乘运算函数dot()

>>> a     #是矩阵形式
matrix([[1, 2],[3, 4]])
>>> a.A   #.A表示 将矩阵a变换成 二维数组
array([[1, 2],[3, 4]])
>>> b.A   #.A表示 将矩阵b变换成 二维数组
array([[0, 1, 2, 3],[4, 5, 6, 7]])#执行矩阵乘法运算--Numpy又称其为点乘运算
>>> np.dot(a.A, b.A)
array([[ 8, 11, 14, 17],[16, 23, 30, 37]])
>>> a.A @ b.A
array([[ 8, 11, 14, 17],[16, 23, 30, 37]])

说明：np.dot()函数可以在两个元素之间用@符号代替，即a@b结果和np.dot(a,b)是一样的。使用a@b这样更简便一些。

3.NumPy中提供的一些其他常用函数

统计函数：sum() 、min()、 max()、 median()、 mean()、 average()、 std()、 var()分别用于求和、求最小值、求最大值、求中位数、求平均数、求加权平均数、求标准差、求方差。
数学函数：三角函数sin() 、cos() 、tan()等。
NumPy提供的函数远不止于此，如果想要娴熟运用它，多查询NumPy的官方帮助文件。