如果你发现某段信号里面有干扰,想要分析这段信号里面的频率成分,就可以使用matlab导入Excel数据后进行快速傅里叶变换(fft)。
先直接上使用方法,后面再补充理论知识。
可以通过串口将需要分析的数据发送到串口助手,注意,串口助手复制数据,是你接收了多少,就能复制多少。
将接收到的数据放到Excel表格中,用一列就可以了,不必给数据列表头起名字。

注意:
为了方便进行 FFT 运算,通常数据数量 取 2 的整数次方。可以加快matlab的分析速度,不是也关系不大。
另外,要去掉这一列数据中的空格,否则matlab无法分析出正确结果,选中这一列,查找全部空格,然后在某一个选中的空格上右键删除行即可删除所有空格。
打开matlab软件,点击导入数据

等待一段时间(根据电脑配置而不同)后,就会出现如下界面
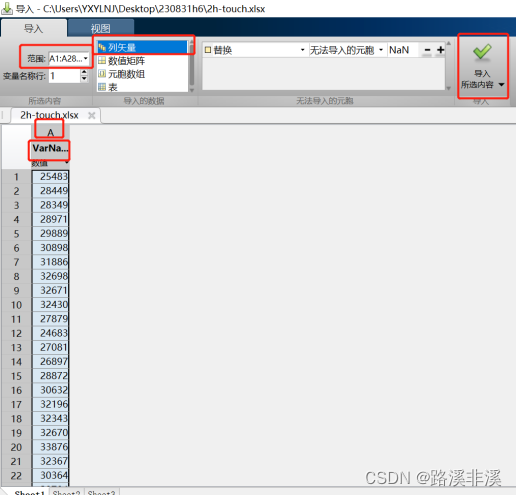
范围:虽然将Excel中的所有数据都导入了,但是可以选择数据范围进行分析,这里就可以选择,Am:An,表示A列的第m到第n个数据。
列矢量:因为只导入了一列,所以选择列矢量即可,网上好多教程都是让导入两列,然后选择数值矩阵,其实没有必要。
VarName:导入一列数据时,该列向量的变量名就是VarName,多个的话就是VarName1、VarName2、VarName3……最多到VarName9,所以,如果超过VarName9,就不能再用VarName这个名称了。不过,我们也可以双击这里的名称,然后修改。
一般情况下,数据导入后,只需要选择性地更改名称即可,其他都是默认选择。
确认无误后,点击绿色对钩导入所选内容,当出现蓝色字提示,就表示数据已经导入了
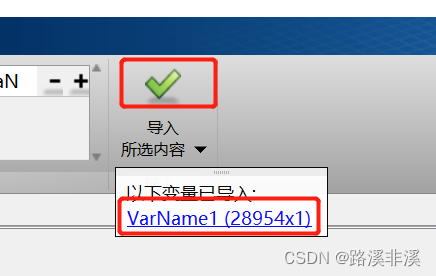
此时,可以在工作区看到该变量名

到了这里,数据已经被导入了。
接下来,就可以进行傅里叶变换,并绘制出幅频图了。
点击新建脚本并保存,然后在脚本中输入以下程序
Fs = 2000;
Y = fft(VarName1);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
axis([0,Fs/2,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');
其中,Y = fft(VarName1);这里的VarName1就是刚才导入的变量名,如果是别的名称,对应起来即可。
选中这些程序,然后右键执行所选内容

稍作等待,就会出现幅频图
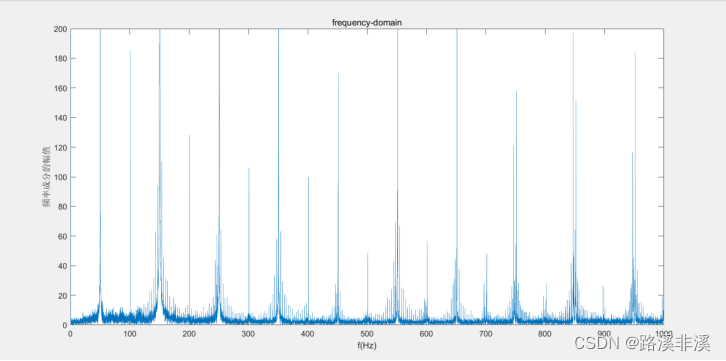
可以看到,这个信号里面,是有很多工频干扰的,而且,干扰的范围还不小。
至此,整个使用过程已结束。
理论知识补充
以上的过程其实就是涉及到DSP数字信号处理的知识。
接下来补充一下理论知识,帮助更好地理解以上内容。
首先,什么是傅里叶变换?
傅立叶变换是一种分析信号的方法,它可分析信号的成分,也可用这些成分合成信号。
想要更好地理解这个问题,可以参考:
傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎
这篇文章形象地讲解了什么是傅里叶级数和傅里叶变换。
摘录精华如下:

简单点来说,就是任一函数都可以展成三角函数的无穷级数
其次,什么是FFT?
FFT 是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
了解了什么是FFT,就能更好地理解一些问题了。
比如,为什么信号有干扰之后数值会变大?
一般,我们看电流或者电压强度,都是看幅值,本来信号值是5,可是采到的却是48,显然太大了,此时,就是因为有其他频率的干扰叠加在了信号上面,导致幅值增大。如果干扰很大,幅值就会增大很多。
所以,就要搞清楚是什么频率的干扰波叠加在信号上面,因此就可以进行fft变换来分析。
幅频图表示什么含义?
横坐标是连续的频率值,纵向就是各频率信号的幅度值,也就是叠加在原始信号上的强度。
注意:我在上面提供的程序所出来的图,因为做了纵向量纲的校准,所以显示的幅值就是频率的实际幅值。
接下来就要重点讲解一下这段程序。
首先,可以看看这几个视频,看完你就会恍然大悟。
NO.12 傅里叶变换频谱图你必须知道的_哔哩哔哩_bilibili
Fs = 2000;
Y = fft(VarName1);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
axis([0,Fs/2,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');
针对这个程序,一句一句地分析。
Fs = 2000;
一开始,这里面有个采样率Fs,是我最不能理解的部分,因为真的很难理解。
我看了很多网络上的讲解,都没有能够讲解Fs这个怎么来的。
而且,这个Fs真的很关键,非常关键。我在实际操作中,只要Fs变了,频率值就变了,比如,原本是50Hz的干扰,如果Fs减半,频率也会减半到25Hz去显示,这样,就会误导我们,到底是什么频率的干扰?非常容易造成误判。
2000的采样率
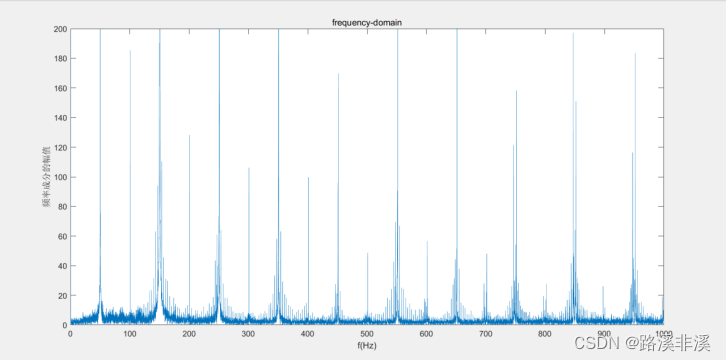
1000的采样率

很明显,虽然总体趋势没变,但是频率从原来的50Hz干扰,变到了25Hz的干扰。
这就已经对我们造成了严重的误导。因为就会导致后面一系列的连锁错误。
这么重要的问题,不知道为什么大家都不讲清楚。
由上面的分析可知,只有唯一一个确定的Fs才能够保证我们的分析结果是正确的。
那这个Fs值到底是多少呢?
这个Fs到底是怎么确定的呢?
一开始,我有好多疑问,Fs是matlab分析所需要的,可以任意取值的吗?上面我们已经证明了并不是随便取值的。
然后,我又想,难道是跟原始信号的频率有关?原始信号有无数个频率叠加,不可能是由它们来确定的。而且,叠加之后的频率也没法确定。
那就是ADC的采样频率?有点接近了,不过我查了一下程序,发现ADC的采样频率对不上。
再理一理思路,有一个原始信号,叠加了很多的干扰信号,我用ADC来采集,采集之后通过串口一个一个地发送到PC,ADC的采样速度比串口的速度要快。假设原始信号最大频率是1000Hz,ADC按照2000Hz去采,采了3000个点,可是串口只每隔2个点上传一次,那采样率就是1000?
最终,我想明白了,我要分析的数据是怎么来的,就看它的最终获取频率。
只需要看最终输出,不管中间经历了多少路径,只看最后收到了多少原始数据,不经过任何处理。
串口是每500us发送一个数据,也就是说,采样率是2000,这是我最终得到的数据采样率,也就是我要分析的数据的采样率。
有三种方式可以验证:
- 更改串口的发送频率来验证;
- 看串口是不是1秒钟接收了那么多数据;
- 可以输入一个有明显幅度的特定频率信号,然后验证设定的采样率下,频率显示是否正确。
其中,第三种方式,是最直观最准确的,推荐使用。
Y = fft(VarName1);
傅里叶变换
将时域数据转换成频域数据,也就是一个一个的频率点,是根据欧拉公式,使用复数来表示的。
时域数据

频域数据

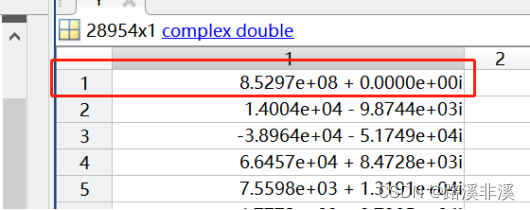
这里是用科学计数法来表示的。
第一个数就是实数,第二个数就是虚数,后面的i是虚数单位。
时域数据和频域数据的数量是一样的。N 个采样点,经过 FFT 之后,就可以得到 N 个点的FFT结果。
频域数据具有对称性和周期性。
L = length(Y);
获取数据的长度,也就是数量。
P2 = abs(Y/L);
P1 = P2(1:L/2+1);%这里加1是为了包含对称性数据的中间数据
P1(2:end-1) = 2*P1(2:end-1);
上面说了,频域数据里就是一个一个频率点的复数表示,这些频率点的强度是多少呢?直接对复数值取模即可,也就是abs(Y);
假设 FFT之后某点 n 用复数 a+bi 表示,那么这个复数的模就是:
![]()
为什么上面要除以L呢?P2 = abs(Y/L);
其实,不是为了除以L,是想除以L/2。
为什么?
FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为 A,那么 FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是 A 的 N/2 倍。 而第一个点就是直流分量,它的模值就是直流分量的 N 倍。
根据这段话可知:点的模值=原始信号的模值*(N/2),所以,点的模值/(N/2),就能获取该频率信号实际的幅度值。
以上是先除以L,再P1(2:end-1) = 2*P1(2:end-1);这里乘以2,就是为了换算成实际的幅值。
而且,P1(2:end-1) = 2*P1(2:end-1);这里从第2点开始是为了将直流分量去掉,因为直流分量不用乘以2,直接除以L即可。这里的end表示最后一个元素索引:

为什么去掉最后一个点,只到end-1。
因为end-1表示对称的最中心数据,该频率点的波形不显示。
说明如下:
fs=1000; %设置采样频率 1k
N=1024; %采样点数
n=0:N-1;
t=0:1/fs:1-1/fs; %时间序列
f=n*fs/N; %频率序列
x1=sin(2*pi*70*t); %噪声
x2=sin(2*pi*200*t); %信号
x3=sin(2*pi*500*t); %信号
x=x1+x2+x3; %信号混合
subplot(311);
plot(t,x); %绘制原始信号
xlabel('时间');
ylabel('幅值');
title('原始信号');
可以看到,500Hz的频率图像没有显示出来。

为什么这里只取一半的值?
要注意,这里并不是取一半的值,而是只取一半的点来分析。这是因为傅里叶变换后的数据具有对称性,后一半的数据不具备实际意义。

接下来的这句f = Fs*(0:(L/2))/L;就是为了适应这一点,这句话实际结果就是0—Fs/2,这句话不是为了取一半的点,而是为了取一半的频率。
FFT 之后结果就是一个为 N 点的复数。每一个点就对应着一个频率点。第一个点表示直流分量(即 0Hz),而最后一个点 N 的再下一个点(实际上这个点是不存在的,这里是假设的第 N+1 个点,可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率 Fs,这中间被 N-1 个点平均分成 N 等份,每个点的频率依次增加。
其实,可以从另一个角度来理解,那就是著名的奈奎斯特采样定律:只要采样频率大于或等于有效信号最高频率的两倍,采样值就可以包含原始信号的所有信息,被采样的信号就可以不失真地还原成原始信号。
一个模拟信号,经过 ADC 采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍。
我们这里的采样率是Fs,所以最大只能采到Fs/2的最大频率信号,那么,高于Fs/2的频率部分其实是没有意义的。
另外,根据上面的频率分布可知道,Fn 所能分辨到频率为 Fs/N,如果采样频率 Fs 为 1024Hz,采样点数为1024点,则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点,刚好是 1 秒,也就是说,采样 1 秒时间的信号并做 FFT,则结果可以分析到 1Hz,如果采样 2 秒时间的信号并做 FFT,则结果可以分析到 0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
所以,如果对分辨率要求不高,就可以少取一些数据。对分辨率要求高,就需要多取一些数据。
由于 FFT 结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
FFT结果的是存在对称性的,这是由FFT计算中隐含的复数运算处理、以及计算是对周期性离散处理(时域、频域转换) 等带来的特性,一般使用时不用详究,只需要知道存在这个特性即可,数据也只需要用任意一半即可(普遍采用前一半)。
具体原因,可自行查找资料。
对称性示例:

注意,对称性不包含第一个直流分量。
附上手写信号测试:
ts = 0:0.01:10;
sig = sin(2*pi*ts) + 5*sin(2*pi*10*ts);
Fs = 100;
Y = fft(sig);
L = length(Y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
plot(f,P1);
%axis([0,1000,0,200]);
title('frequency-domain');
xlabel('f(Hz)');
ylabel('频率成分的幅值');