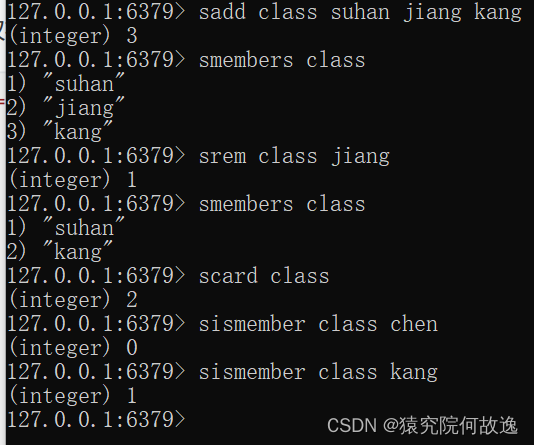
在模态分析中，所研究的系统通常表示为一组质量、刚度和阻尼元件（在下面的文章中忽略了阻尼）。通过求解系统的运动方程，可以确定系统振动的固有频率以及相应的振型或运动模式。

        固有频率表示系统在被激发或干扰时倾向于振动的频率。每个固有频率对应于一种振动模式，该振动模式是与特定频率相关的独特运动模式。振型描述了系统在每种振动模式下的移动和变形方式。

        模态分析通常用于各个领域，包括结构工程、机械工程、航空航天工程和声学。它在结构设计、隔振、噪声控制和故障分析等领域都有应用。通过了解系统的自然模式，工程师可以设计不易产生共振的结构，优化性能，并识别潜在问题，如弱点或过度振动。

二、直觉

          我们可以接收到我们相关的模态分析和傅里叶分析的模式感，此外还有不同的概念。

        模态分析侧重于将振动系统的运动分解为其单独的振动模式。每种模式代表具有特定固有频率和相应振幅的独特运动模式。通过确定固有频率和振型，模态分析使我们能够理解和分析系统的动态行为。

        另一方面，傅里叶分析是一种数学技术，用于将复杂信号分解为更简单的正弦分量的总和。它表示频域中的信号，其中每个正弦分量对应于特定的频率和幅度。傅里叶分析通常用于信号处理、频谱分析以及时域和频域之间的转换信号。

        虽然模态分析和傅里叶分析都涉及将信号分解为更简单的分量，但基本原理和目标是不同的。模态分析侧重于物理系统的固有振动模式，而傅里叶分析则处理信号的频谱分解为正弦分量。

        总之，虽然模态分析和傅里叶分析在分解信号方面有一些相似之处，但它们是用于不同目的的不同技术。模态分析特别关注物理系统的振动行为，而傅里叶分析是用于分析频域信号的更通用的数学工具。

        请注意，该模式是指振动系统表现出的特定运动模式。每种模式都与独特的位移组合相关联，并对应于固有频率。
        固有频率是系统的固有属性，由其质量、刚度和几何形状决定。固有频率表示系统在没有任何外部强迫的情况下被激励或干扰时倾向于振动的频率。系统中的每种振动模式都有其相应的固有频率。
        然而，共振频率是系统在受到外部激励（力）时表现出最强响应或放大的频率。当激励频率匹配或接近系统的固有频率时，就会发生这种情况。由于激励和系统之间的能量有效传递，共振会导致更大的振动幅度。
        在模态分析的上下文中，特征值是通过求解系统的特征方程获得的参数。特征方程与系统的动态行为有关，涉及刚度和质量矩阵。特征值表示特征方程的根，并确定系统的固有频率。每个特征值对应于特定的振动模式，并表示该模式振动的频率。

三、模态分析概述

        拉格朗日方程描述的机械系统可能难以求解，因为方程通常是耦合的。这意味着一个组件的运动或行为会影响其他组件的运动。

        在耦合系统中，不能为每个分量独立求解运动方程。这些方程通过涉及多个分量的位移、速度、加速度或力的项相互关联。

        耦合可能是由于系统不同部分之间的物理相互作用或连接而发生的，例如弹簧、阻尼器或相互依赖的力。

        求解耦合系统涉及考虑方程的相互依赖性并同时求解它们，以获得满足组件之间相互作用的完整解。这可能比求解非耦合方程组更复杂，其中每个方程都可以独立求解。

        对于这样的系统，我们经常使用模态分析，它通常旨在解耦运动方程，并以独立的振动模式来表达它们。这简化了分析，并允许单独检查每个模式（在模态坐标中）。

        下图提供了模态分析的一般概述。

四、吸收器设计和模拟

        为了简化设计分析，让我们考虑质量 1 受到周期性力 F 的场景。该力影响质量1的运动。吸收器质量2分量通过弹簧连接到质量1的目的是减少这些运动。

        我们系统的模型可以呈现如下。

        动态方程，我通过应用Ruge-Kutta方法求解。

        我们的目标是找到质量 2 的某些条件（质量和弹簧刚度值），这些条件会影响质量 1 保持静止。

        动力学方程相对简单，因此不需要模态分析。尽管如此，在所讨论的模型分析中概述主要步骤以充分结束我们的讨论将是有益的。

        程序如下。对于我们的系统（运动方程），我们需要解决特征值问题。这意味着我们需要确定模态频率（特征值）和振型（特征向量）。我在 Python 中解决了这个讨论的方程，并确定了两对特征值和特征向量。
        稍后计算的特征值和向量，我们应用来查找系统的模态。最后，我们可以指定系统的模式如下（有关更多详细信息，请参阅此处 )

        模式 1

        模式 2

        现在我们必须分析整个系统的响应。我们将早期的计算模式相加并绘制绝对值。

        在分析该图时，很明显存在某些不同的频率，其中质量1的运动可以忽略不计，导致其保持静止。这个特定的频率被称为反共振频率（这里为15rad / s）。

        为了创建详细设计，我们遵循求解拉格朗日运动方程的标准方法，以找到相应的解。这个方程的解是谐波，可以表示如下：

        有了这个谐波解，我们可以很容易地计算速度和加速度，并将它们代入我们的拉格朗日运动方程。

        通过应用一些基本的代数，我们可以将方程简化为以下形式：

        为了找到质量 1 保持静止的条件，我们将求解给定方程中的 Y = 0。

        通过代入这些值，我们可以确定质量 2 的设计条件和弹簧 2 的刚度，以满足所需的频率平方。也可以确定质量 2 位移。我们的设计标准如下：

        我们可以再次使用运动方程，并应用设计条件来正确设计吸收器。
假设质量 1 和质量 2 之间存在一个因子（通常比率为 0.1），我们可以指定主频率（对于质量 1）。

        代数计算得出一个方程，其中如果欧米茄等于欧米茄 （*），则质量 1 保持不变。

        绘制此关系将生成与模型分析中预期的相同的图。
        在频率等于15rad/s时，我们可以消除质量1（Y=0）的运动。有了质量 1 和质量 2 的比例因子，我们可以很容易地找到 k2 的刚度

        我们可以根据设计标准模拟两个质量的运动，其中我们计算 k2 的刚度以消除质量 1 运动。

        你可以在我的GitHub上找到源代码。

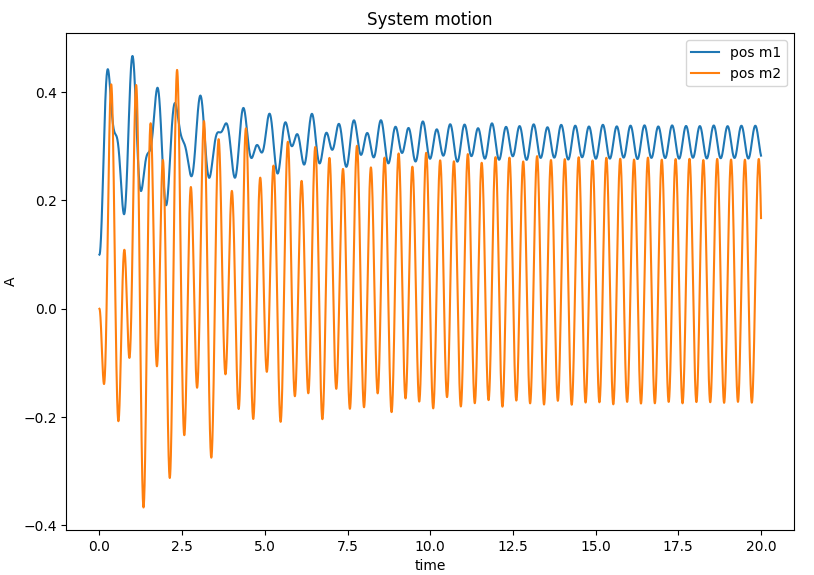
        m1的运动几乎被移除（作者）

        正如预期的那样，阻尼器消除了质量 1 上的（几乎）运动。