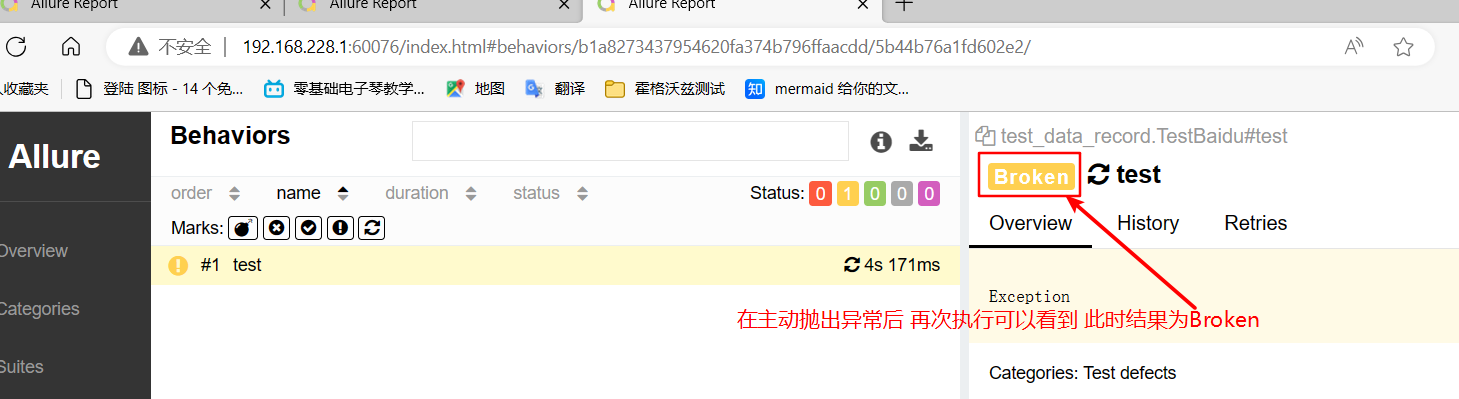
需求需要缓存这个出入记录，当tab切换时不重新加载，当刷新页面时，或把这个关闭在重新打开时重新加载如图：

（我这里用的是芋道源码的前端框架)

keep-alive

1、include 包含页面组件name的这些组件页面，会被缓存起来
2、exclude 除了这些name以外的页面组件，会被缓存起来
3、没有include或者exclude属性，表示所有的路由组件都会被缓存起来

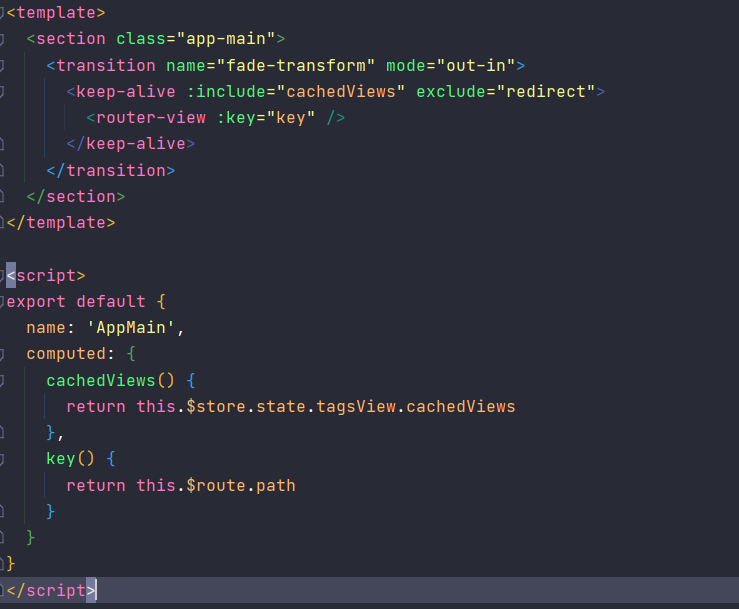
<template><section class="app-main"><transition name="fade-transform" mode="out-in"><keep-alive :include="cachedViews" exclude="redirect"><router-view :key="key" /></keep-alive></transition></section>
</template><script>
export default {name: 'AppMain',computed: {cachedViews() {return this.$store.state.tagsView.cachedViews},key() {return this.$route.path}}
}
</script>

解决方法

现在router里面的index.js里面把这三个路由写出来

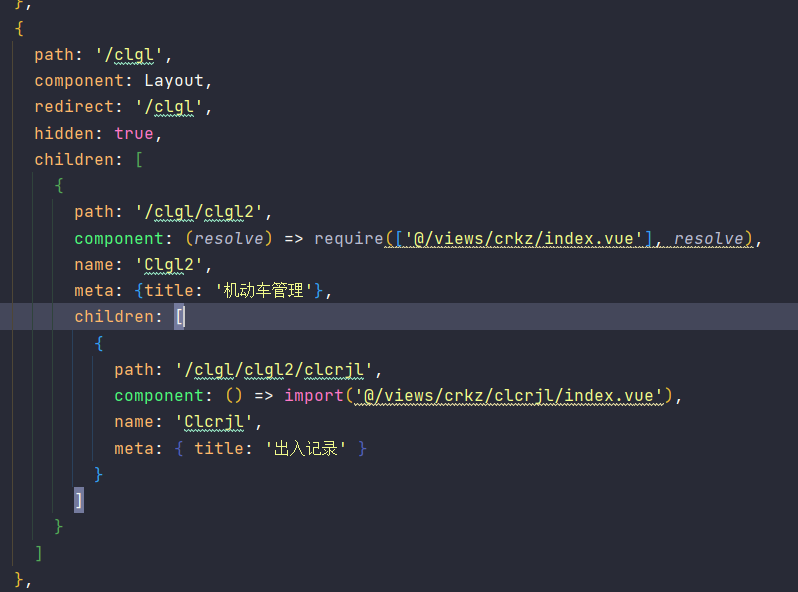
然后在仓库里面手动把二级路由加上

这样就可以了