duffing混沌振子形式如下:
k,a,c,f为自定义系数,将初值设为,k=0.5,a=c=1
此时可通过更改f的值从0到1来改变duffing混沌系统状态,从固定点状态,小周期状态,混沌状态到大周期状态。例如f=0.6时处于混沌状态,如下:
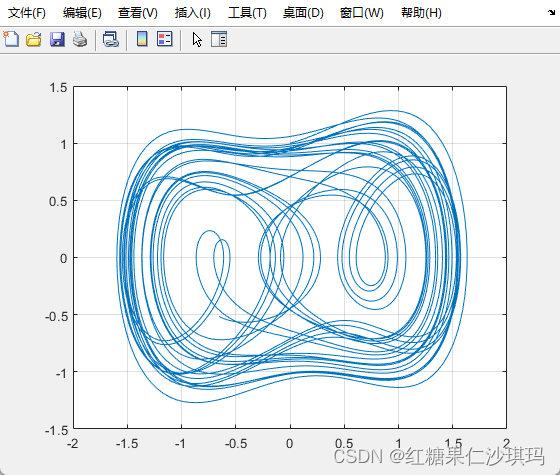
上图横坐标x,纵坐标x的一阶导数

上图横坐标为时间t,纵坐标x
clc;clear;
[x,y]=ode113(@duffingFunc,[0:0.05:200],[0;1]);
figure(1);
plot(x,y(:,1));
grid on;
figure(2);
plot(y(:,1),y(:,2));
grid on;
function res=duffingFunc(x,y)k=0.5;a=1;c=1;f=0.75;res=zeros(2,1);res(1)=y(2);res(2)=a*y(1)-c*y(1)^3-k*y(2)+f*cos(x);
end求解利用matlab中的ode113函数,duff ingFunc函数步骤为
利用四阶龙格库塔绘制,y3=t先转化三阶自治系统
clc;clear;format long;
h=0.005;%步长
iters=50000;%迭代次数
ys=zeros(3,iters);
y1=1;y2=1;y3=0;
for i=1:iters[y1n,y2n,y3n]=myfunc(y1,y2,y3,h);y1=y1n;y2=y2n;y3=y3n;ys(1,i)=y1;ys(2,i)=y2;ys(3,i)=y3;
end
figure();
plot(1:iters,ys(1,:));
hold on;
plot(1:iters,ys(2,:));
legend("y1","y2");
figure();
plot(ys(3,:),ys(1,:));
figure();
plot(ys(1,:),ys(2,:));
function [y1n,y2n,y3n]=myfunc(y1,y2,y3,h)
f=0.9;
ky1_1=y2;
ky2_1=-0.5*y2+y1-y1^3+0.6*sin(y3);
ky3_1=1;ky1_2=y2+ky1_1*h/2;
ky2_2=-0.5*(y2+ky2_1*h/2)+(y1+ky1_1*h/2)-(y1+ky1_1*h/2)^3+f*sin(y3+ky3_1*h/2);
ky3_2=1;ky1_3=y2+ky1_2*h/2;
ky2_3=-0.5*(y2+ky2_2*h/2)+(y1+ky1_2*h/2)-(y1+ky1_2*h/2)^3+f*sin(y3+ky3_2*h/2);
ky3_3=1;ky1_4=y2+ky1_3*h;
ky2_4=-0.5*(y2+ky2_3*h)+(y1+ky1_3*h)-(y1+ky1_3*h)^3+f*sin(y3+ky3_1*h/2);
ky3_4=1;y1n=y1+h*(ky1_1+2*ky1_2+2*ky1_3+ky1_4)/6;
y2n=y2+h*(ky2_1+2*ky2_2+2*ky2_3+ky2_4)/6;
y3n=y3+h*(ky3_1+2*ky3_2+2*ky3_3+ky3_4)/6;
end