学习二叉树之前先学习树的概念。

1. 树的基本概念

之前所学均为线性表，线性表具有什么特点呢？
第一个节点只有一个后继结点，没有前驱，最后一个节点，只有一个前驱，没有后继，其他位置的节点都有前驱和后继。
线性表中每个节点之间都是一对一的关系，存储也就相对容易一些。

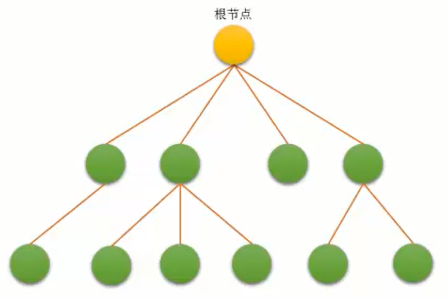
下图就是一个树的结构，每一个节点是一对多的关系，每一个节点都有一个双亲节点（父节点、爹妈节点），但是有多个后继，这就是树概念。

1.1 树的定义

由一个或多个(n≥0)结点组成的有限集合 T，有且仅有一个结点称为根(root)，当n>1时，其余的结点分为m(m≥0)个互不相交的有限集合 T1,T2，…，Tm。每个集合本身又是棵树，被称作这个根的子树。

1.2 树的特点

• 非线性结构，有一个直接前驱，但可能有多个直接后继(1:n )
• 树的定义具有递归性，树中还有树。
• 树可以为空，即节点个数为 0。

1.3 若干术语

• 根–>即根结点(没有前驱)
• 叶子–>即终端结点(没有后继)
• 森林–>指 m 棵不相交的树的集合(例如删除 A 后的子树个数)
• 有序数–>结点各子树从左至右有序，不能互换(左为第一)
• 无序树–>结点各子树可互换位置。
• 双亲–>即上层的那个结点(直接前驱) parent
• 孩子–>即下层结点的子树(直接后继) child
• 兄弟–>同一双亲下的同层结点(孩子之间互称兄弟) sibling
• 堂兄弟–>即双亲位于同一层的结点(但并非同一双亲)cousin
• 祖先–>即从根到该结点所经分支的所有结点
• 子孙–>即该结点下层子树中的任一结点
  
• 结点–>即树的数据元素
• 结点的度–>结点挂接的子树数( 有几个直接后继就是几度 )
• 结点的层次–>从根到该结点的层数( 根结点算第一层 )
• 终端结点–>即度为 0 的结点，即叶子
• 分支结点–>除树根以外的结点( 也称为内部结点)
• 树的度–>所有结点度中的最大值( Max(各结点的度》)
• 树的深度(或高度)–>所有结点中最大的层数( Max(各结点的层次))
  上图中的结点数= 13，树的度= 3，树的深度= 4

2. 树的表示法

2.1 图形表示法

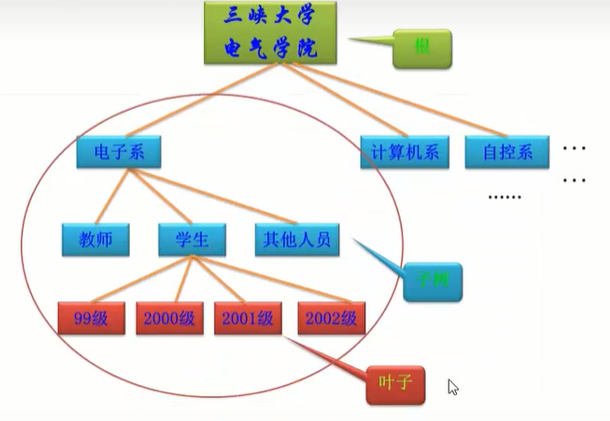
事物之间的逻辑关系可以通过数的形式很直观的表示出来，如下图：

2.2 广义表表示法

用广义表表示法表示上图:
中国( 河北( 保定，石家庄 )，广东( 广州，东莞 )，山东( 青岛，济南 ) )
根作为由子树森林组成的表的名字写在表的左边。

3. 树的存储

前面我们学习了顺序存储和链式存储，以下面的树为例，如何进行存储呢？也可以使用顺序存储：A,B,C,D...M，放到数组中，但是你不知道谁是谁儿子和爹吗？

3.1 双亲表示法：保存父节点关系

了解即可

struct Node {int data; //节点值int parent; //父节点下标
}

为了找到某一个节点的孩子是谁，需要进行遍历查看父节点信息。
上面的方法是站在爹妈的角度去看的

3.2 孩子表示法

以孩子成长的角度来看就是孩子表示法。以链式去保存，需要保存孩子的信息，但是孩子数量不固定，对于ChildNode*就不知道定义几个指针了，定义的多了就会产生多余指针。

可以通过链表将孩子节点进行保存，这样就可以通过链表将节点进行保存

struct ChildNode {int data; //节点值ChildNode*
}
childNode D;
D.ChildNode*;

3.3 左孩子右兄弟表示法

不管是什么样的树，都可以转换为二叉树

第一个节点A，左孩子为B，右兄弟没有，B的左孩子E，右兄弟C，E的左孩子K，右兄弟F，K的左孩子没有，右兄弟L，到F，左孩子和右兄弟没有，到C，左孩子G，右兄弟D，D的左孩子H，右兄弟没有，到H，左孩子M，右兄弟I，I的左孩子没有，右兄弟J。

通过左孩子右兄弟之后就转换为这种树，每个节点有0到2个孩子，这种树称为二叉树。