一、前言

二、实验环境

三、NumPy

0、多维数组对象（ndarray）

多维数组的属性

1、创建数组

2、数组操作

3、数组数学

1. 元素级别

a. 直接运算

b. 加法：np.add()函数

c. 减法：np.subtract()函数

d. 乘法：np.multiply()函数

e. 除法：np.divide()函数

f. 幂运算：np.power()函数

g. 取余与求商：

2. 数组级别

a. 平均值：np.mean()

b. 最大值和最小值：np.max()、np.min()

c. 求和：np.sum()

d. 标准差和方差：np.std()、np.var()

3. 矩阵级别

a. 矩阵乘法

b. 矩阵转置

c. 矩阵求逆

d. 行列式

e. 特征值和特征向量

f. 矩阵的迹

g. 点积

4. 其他数学函数

a. 三角函数

b. 指数和对数函数

c. 取整函数

d. 绝对值

e. 累加和和累积

一、前言

Python是一种高级编程语言，由Guido van Rossum于1991年创建。它以简洁、易读的语法而闻名，并且具有强大的功能和广泛的应用领域。Python具有丰富的标准库和第三方库，可以用于开发各种类型的应用程序，包括Web开发、数据分析、人工智能、科学计算、自动化脚本等。

Python本身是一种伟大的通用编程语言，在一些流行的库（numpy，scipy，matplotlib）的帮助下，成为了科学计算的强大环境。本系列将介绍Python编程语言和使用Python进行科学计算的方法，主要包含以下内容：

Python：基本数据类型、容器（列表、元组、集合、字典）、函数、类
Numpy：数组创建、数组操作、数组数学、广播
Matplotlib：绘图，子图，图像
IPython：创建笔记本，典型工作流程

二、实验环境

numpy	1.21.6
python	3.7.16

运行下述命令检查Python版本

 python --version

运行下述代码检查Python、NumPy版本

import sys
import numpy as npprint("Python 版本:", sys.version)
print("NumPy 版本:", np.__version__)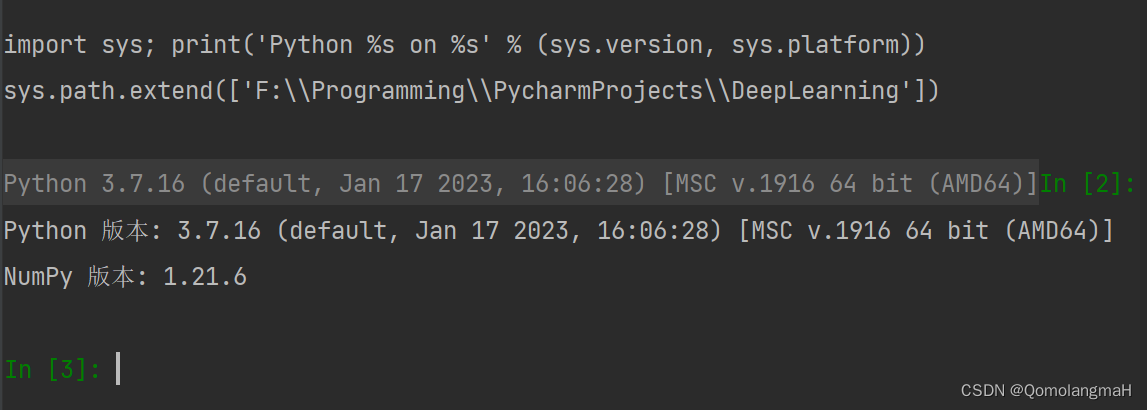

三、NumPy

NumPy（Numerical Python）是一个用于科学计算的Python库。它提供了一个强大的多维数组对象（ndarray），用于进行高效的数值运算和数据处理。Numpy的主要功能包括：

多维数组：Numpy的核心是ndarray对象，它是一个多维数组，可以存储同类型的元素。这使得Numpy非常适合处理向量、矩阵和其他多维数据结构。

数学函数：Numpy提供了许多常用的数学函数，如三角函数、指数函数、对数函数等。这些函数可以直接应用于整个数组，而无需编写循环。

广播（Broadcasting）：Numpy支持不同形状的数组之间的运算，通过广播机制，可以对形状不同的数组进行逐元素的操作，而无需显式地编写循环。

线性代数运算：Numpy提供了丰富的线性代数运算函数，如矩阵乘法、求解线性方程组、特征值计算等。

随机数生成：Numpy包含了用于生成各种概率分布的随机数的函数，如均匀分布、正态分布、泊松分布等。

数据操作：Numpy提供了很多用于操作数组的函数，如切片、索引、排序、去重等。

Numpy广泛应用于科学计算、数据分析、机器学习等领域。它的高效性和便捷性使得它成为Python数据科学生态系统中不可或缺的组成部分。

0、多维数组对象（ndarray）

NumPy的ndarray对象是NumPy库中最重要的对象之一，也是进行科学计算的核心数据结构。ndarray代表了一个多维的数组，可以存储相同类型的元素。

多维数组的属性

ndarray.shape：返回表示数组形状的元组，例如(2, 3)表示2行3列的数组。
ndarray.dtype：返回数组中元素的数据类型，例如int、float、bool等。
ndarray.ndim：返回数组的维度数，例如1表示一维数组，2表示二维数组。

1、创建数组

【深度学习】 Python 和 NumPy 系列教程（九）：NumPy详解：1、创建数组的n种方式_QomolangmaH的博客-CSDN博客https://blog.csdn.net/m0_63834988/article/details/132782221?spm=1001.2014.3001.5501

2、数组操作

【深度学习】 Python 和 NumPy 系列教程（十）：NumPy详解：2、数组操作（索引和切片、形状操作、转置操作、拼接操作）_QomolangmaH的博客-CSDN博客https://blog.csdn.net/m0_63834988/article/details/132830547?spm=1001.2014.3001.5501

3、数组数学

1. 元素级别

NumPy提供了许多在数组元素级别进行数学运算的函数，例如加法、减法、乘法、除法、幂运算等。这些函数会对数组中的每个元素进行相应的数学计算，并返回一个新的数组作为结果。

a. 直接运算

import numpy as nparr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])# 加法
result = arr1 + arr2
print(result)  # 输出: [5 7 9]# 减法
result = arr1 - arr2
print(result)  # 输出: [-3 -3 -3]# 乘法
result = arr1 * arr2
print(result)  # 输出: [4 10 18]# 除法
result = arr1 / arr2
print(result)  # 输出: [0.25 0.4  0.5]

b. 加法：`np.add()`函数

import numpy as nparr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])# 数组元素级别的加法
result = np.add(arr1, arr2)
print(result)

输出：

[5 7 9]

c. 减法：`np.subtract()`函数

import numpy as nparr1 = np.array([4, 5, 6])
arr2 = np.array([1, 2, 3])# 数组元素级别的减法
result = np.subtract(arr1, arr2)
print(result)

输出：

[3 3 3]

d. 乘法：`np.multiply()`函数

import numpy as nparr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])# 数组元素级别的乘法
result = np.multiply(arr1, arr2)
print(result)

输出：

[ 4 10 18]

e. 除法：`np.divide()`函数

import numpy as nparr1 = np.array([4, 6, 8])
arr2 = np.array([2, 3, 4])# 数组元素级别的除法
result = np.divide(arr1, arr2)
print(result)

输出：

[2. 2. 2.]

f. 幂运算：`np.power()`函数

import numpy as nparr = np.array([1, 2, 3])# 数组元素级别的幂运算
result = np.power(arr, 2)
print(result)

输出：

[1 4 9]

g. 取余与求商：

import numpy as nparr1 = np.array([7, 8, 9])
arr2 = np.array([2, 3, 4])# 数组的取余
result = np.mod(arr1, arr2)
print(result)  # 输出: [1 2 1]# 数组的求商
result = np.divmod(arr1, arr2)
print(result)  # 输出: (array([3, 2, 2]), array([1, 2, 1]))

2. 数组级别

a. 平均值：`np.mean()`

import numpy as nparr = np.array([1, 2, 3, 4, 5])# 计算数组的平均值
mean_value = np.mean(arr)
print(mean_value)

输出：

3.0

b. 最大值和最小值：`np.max()、np.min()`

使用np.max()和np.min()函数分别计算数组的最大值和最小值。

import numpy as nparr = np.array([1, 2, 3, 4, 5])# 计算数组的最大值和最小值
max_value = np.max(arr)
min_value = np.min(arr)print(max_value, min_value)

输出：

5 1

c. 求和：`np.sum()`

计算数组所有元素的和

import numpy as nparr = np.array([1, 2, 3, 4, 5])# 计算数组的元素和
sum_value = np.sum(arr)
print(sum_value)

输出：

d. 标准差和方差：`np.std()`、`np.var()`

使用np.std()和np.var()函数计算数组的标准差和方差

import numpy as nparr = np.array([1, 2, 3, 4, 5])# 计算数组的标准差和方差
std_value = np.std(arr)
var_value = np.var(arr)print(std_value, var_value)

输出：

1.4142135623730951 2.0