目录
蓝桥杯2023年第十四届省赛真题-更小的数
题目描述
输入格式
输出格式
样例输入
样例输出
提示
【思路解析】
【代码实现】
蓝桥杯2023年第十四届省赛真题-更小的数
时间限制: 3s 内存限制: 320MB 提交: 895 解决: 303
题目描述
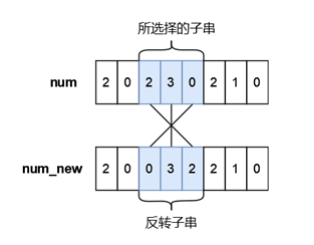
小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串,下标从 0 到 n − 1,你可以将其视作是一个具有 n 位的十进制数字 num,小蓝可以从 num 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num,请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 ,这是合法的。
输入格式
输入一行包含一个长度为 n 的字符串表示 num(仅包含数字字符 0 ∼ 9),
从左至右下标依次为 0 ∼ n − 1。
输出格式
输出一行包含一个整数表示答案。
样例输入
复制
210102
样例输出
复制
8
提示
一共有 8 种不同的方案:
1)所选择的子串下标为 0 ∼ 1 ,反转后的 numnew = 120102 < 210102 ;
2)所选择的子串下标为 0 ∼ 2 ,反转后的 numnew = 012102 < 210102 ;
3)所选择的子串下标为 0 ∼ 3 ,反转后的 numnew = 101202 < 210102 ;
4)所选择的子串下标为 0 ∼ 4 ,反转后的 numnew = 010122 < 210102 ;
5)所选择的子串下标为 0 ∼ 5 ,反转后的 numnew = 201012 < 210102 ;
6)所选择的子串下标为 1 ∼ 2 ,反转后的 numnew = 201102 < 210102 ;
7)所选择的子串下标为 1 ∼ 4 ,反转后的 numnew = 201012 < 210102 ;
8)所选择的子串下标为 3 ∼ 4 ,反转后的 numnew = 210012 < 210102 ;
对于 20% 的评测用例,1 ≤ n ≤ 100 ;
对于 40% 的评测用例,1 ≤ n ≤ 1000 ;
对于所有评测用例,1 ≤ n ≤ 5000 。
【思路解析】
遍历所有可能性,对于一个子串 i -- j,有3种情况。
(1)如果str[i] > str[j],可以交换。
(2) 如果str[i] < str[j],不可以交换。
(3)如果str[i] == str[j],则考虑 子串 i+1 --- j-1,可不可以被交换,如果可以交换,则原子串可以交换,否则不可以被交换。
【代码实现】
import java.util.Scanner;/*** @ProjectName: study3* @FileName: Ex2* @author:HWJ* @Data: 2023/9/17 9:22*/
public class Ex2 {static int ans = 0;public static void main(String[] args) {Scanner input = new Scanner(System.in);String s = input.next();char[] str = s.toCharArray();for (int right = 1; right < str.length; right++) {for (int left = 0; left < right; left++) {int L = left + 1;int R = right - 1;boolean loop = false;while (L < R){if(str[L] > str[R]){loop = true;break;} else if (str[L] < str[R]) {break;}else {L += 1;R -= 1;}}if (str[left] > str[right] || (loop && str[left] == str[right])){ans++;}}}System.out.println(ans);}}