双连通分量：判定准则

考查无向图G。若删除顶点v后G所包含的连通域增多，则v称作切割节点或关节点。
不含任何关节点的图称作双连通图。
任一无向图都可视作由若干个极大的双连通子图组合而成，这样的每一子图都称作原图的一个双连通域。

如何才能找出图中的关节点呢？
1.蛮力算法
首先，通过BFS或DFS搜索统计出图G所含连通域的数目；然后逐一枚举每个顶点v，暂时将其从图G中删去，并再次通过搜索统计出图G\{v}所含连通域的数目。于是，顶点v是关节点，当且仅当图G\{v}包含的连通域多于图G。这一算法需执行n趟搜索，耗时O(n(n + e))。
2.可行算法
DFS树中的叶节点，绝不可能是原图中的关节点，此类顶点的删除既不致影响DFS树的连通性，也不致影响原图的连通性。
此外，DFS树的根节点若至少拥有两个分支，则必是一个关节点。
在DFS搜索过程记录并更新各顶点v所能（经由后向边）连通的最高祖先，即可及时认定关节点，并报告对应的双连通域。

节点C的移除导致其某一棵（比如以D为根的）真子树与其真祖先（比如A）之间无法连通，则C必为关节点。反之，若C的所有真子树都能（如以E为根的子树那样）与C的某一真祖先连通，则C就不可能是关节点。C的真子树只可能通过后向边与C的真祖先连通。

双连通分量分解：算法

template <typename Tv, typename Te> void Graph<Tv, Te>::bcc(int s) { //基于DFS的BCC分解算法reset(); int clock = 0; int v = s; Stack<int> S; //栈S用以记录已访问的顶点doif (UNDISCOVERED == status(v)) { //一旦发现未发现的顶点（新连通分量）BCC(v, clock, S); //即从该顶点出发启劢一次BCCS.pop(); //遍历返回后，弹出栈中最后一个顶点——当前连通域的起点}while (s != (v = (++v % n)));
}
#define hca(x) (fTime(x)) //利用此处闲置的fTime[]充当hca[]
template < typename Tv, typename Te> //顶点类型、边类型
void Graph<Tv, Te>::BCC(int v, int& clock, Stack<int>&S) { //assert: 0 <= v < nhca(v) = dTime(v) = ++clock; status(v) = DISCOVERED; S.push(v); //v被发现并入栈for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u)) //枚举v的所有邻居uswitch (status(u)) { //并视u的状态分别处理case UNDISCOVERED:parent(u) = v; type(v, u) = TREE; BCC(u, clock, S); //从顶点u处深入if (hca(u) < dTime(v)) //遍历返回后，若发现u（通过后向边）可指向v的真祖先hca(v) = min(hca(v), hca(u)); //则v亦必如此else { //否则，以v为关节点（u以下即是一个BCC，且其中顶点此时正集中于栈S的顶部）while (v != S.pop()); //依次弹出当前BCC中的节点，亦可根据实际需求转存至其它结构S.push(v); //最后一个顶点（兲节点）重新入栈——总计至多两次}break;case DISCOVERED:type(v, u) = BACKWARD; //标记(v, u)，并按照“越小越高”的准则if (u != parent(v)) hca(v) = min(hca(v), dTime(u)); //更新hca[v]break;default: //VISITED (digraphs only)type(v, u) = (dTime(v) < dTime(u)) ? FORWARD : CROSS;break;}status(v) = VISITED; //对v的访问结束
}
#undef hca

由于处理的是无向图，故DFS搜索在顶点v的孩子u处返回之后，通过比较hca[u]与dTime[v]的大小，即可判断v是否关节点。
这里将闲置的fTime[]用作hca[]。
故若hca[u] ≥ dTime[v]，则说明u及其后代无法通过后向边与v的真祖先连通，故v为关节点。既然栈S存有搜索过的顶点，与该关节点相对应的双连通域内的顶点，此时都应集中存放于S顶部，故可依次弹出这些顶点。v本身必然最后弹出，作为多个连通域的联接枢纽，它应重新进栈。
反之若hca[u] < dTime[v]，则意味着u可经由后向边连通至v的真祖先。果真如此，则这一性质对v同样适用，故有必要将hca[v]，更新为hca[v]与hca[u]之间的更小者。
当然，每遇到一条后向边(v, u)，也需要及时地将hca[v]，更新为hca[v]与dTime[u]之
间的更小者，以保证hca[v]能够始终记录顶点v可经由后向边向上连通的最高祖先。

时间复杂度
与基本的DFS搜索算法相比，这里只增加了一个规模O(n)的辅助栈，故整体空间复杂度仍为O(n + e)。
时间方面，尽管同一顶点v可能多次入栈，但每一次重复入栈都对应于某一新发现的双连通域，与之对应地必有至少另一顶点出栈且不再入栈。因此，这类重复入栈操作不会超过n次，入栈操作累计不超过2n次，故算法的整体运行时间依然是O(n + e)。

优先级搜索

BFS搜索会优先考查更早被发现的顶点，而DFS搜索则恰好相反，会优先考查最后被发现的顶点。
每一种选取策略都等效于，给所有顶点赋予不同的优先级，而且随着算法的推进不断调整；而每一步迭代所选取的顶点，都是当时的优先级最高者。
按照这种理解，包括BFS和DFS在内的几乎所有图搜索，都可纳入统一的框架。鉴于优先级在其中所扮演的关键角色，故亦称作优先级搜索（priority-first search, PFS），或最佳优先搜索（best-first search, BFS）。

template <typename Tv, typename Te> template <typename PU> //优先级搜索（全图）
void Graph<Tv, Te>::pfs ( int s, PU prioUpdater ) { //assert: 0 <= s < nreset(); int v = s; //初始化do //逐一检查所有顶点if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点PFS ( v, prioUpdater ); //即从该顶点出发启动一次PFSwhile ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}template <typename Tv, typename Te> template <typename PU> //顶点类型、边类型、优先级更新器
void Graph<Tv, Te>::PFS ( int s, PU prioUpdater ) { //优先级搜索（单个连通域）priority ( s ) = 0; status ( s ) = VISITED; parent ( s ) = -1; //初始化，起点s加至PFS树中while ( 1 ) { //将下一顶点和边加至PFS树中for ( int w = firstNbr ( s ); -1 < w; w = nextNbr ( s, w ) ) //枚举s的所有邻居wprioUpdater ( this, s, w ); //更新顶点w癿优先级及其父顶点for ( int shortest = INT_MAX, w = 0; w < n; w++ )if ( UNDISCOVERED == status ( w ) ) //从尚未加入遍历树的顶点中if ( shortest > priority ( w ) ) //选出下一个{ shortest = priority ( w ); s = w; } //优先级最高的顶点sif ( VISITED == status ( s ) ) break; //直至所有顶点均已加入status ( s ) = VISITED; type ( parent ( s ), s ) = TREE; //将s及不其父的联边加入遍历树}
} //通过定义具体的优先级更新策略prioUpdater，即可实现不同的算法功能

PFS搜索的基本过程和功能与常规的图搜索算法一样，也是以迭代方式逐步引入顶点和边，最终构造出一棵遍历树（或者遍历森林）。如上所述，每次都是引入当前优先级最高（优先级数最小）的顶点s，然后按照不同的策略更新其邻接顶点的优先级数。

复杂度
PFS搜索由两重循环构成，其中内层循环又含并列的两个循环。若采用邻接表实现方式，同时假定prioUpdater()只需常数时间，则前一内循环的累计时间应取决于所有顶点的出度总和，即O(e)；后一内循环固定迭代n次，累计O(n^ 2时间。两项合计总体复杂度为O(n^2)。

Dijkstra 算法（最短路径）

设顶点s到v的最短路径为ρ。于是对于该路径上的任一顶点u，若其在ρ上对应的前缀为σ，则σ也必是s到u的最短路径（之一）。否则，若从s到u还有另一严格更短的路径τ，则易见ρ不可能是s到v的最短路径。
最短路径的任一前缀也是最短路径

歧义性： 首先，即便各边权重互异，从s到v的最短路径也未必唯一。另外，当存在非正权重的边，并导致某个环路的总权值非正时，最短路径甚至无从定义。

无环性： 路径的并集必然不含任何（有向）回路。

Dijkstra 算法

Dijkstra 算法是一种用于找到带权有向图中从一个起点到所有其他节点的最短路径的算法。该算法使用了贪心策略，逐步构建最短路径树，从起点开始，每次选择距离起点最近的未访问节点作为下一个中间节点，并更新从起点到每个节点的最短距离。Dijkstra算法适用于边的权值为非负数的情况。

template <typename Tv,typename Te> struct DijkstraPU {	//针对Dijkstra算法的顶点优先级更新器virtual void operator() ( Graph<Tv，Te>* g, int uk, int v ) {if ( UNDISCOVERED == g->status ( v ))	//对于uk每一尚未被发现的邻接顶点v，按Dijkstra策略if ( g->priority ( v ) > g->priority ( uk ) + g->weight ( uk,v ) ){	//做松弛g->priority ( v ) = g->priority ( uk ) + g->weight ( uk,v );	//更新优先级（数)g->parent ( v ) = uk; //并同时更新父节点}}
};

实例

1.初始化一个距离数组，表示从起点到每个节点的最短距离，初始值为无穷大，起点的距离为0。
2.创建一个优先队列（最小堆），用于选择下一个中间节点。将起点放入队列。
3.进入循环，直到优先队列为空：
a. 从优先队列中取出距离起点最近的节点（当前中间节点）。
b. 对于当前中间节点的所有邻居节点，计算从起点经过当前中间节点到达邻居节点的距离，并更新距离数组中的值。
c. 如果更新后的距离小于距离数组中原有的值，将邻居节点及其新距离放入优先队列中。
4.循环结束后，距离数组中存储了从起点到所有节点的最短距离。

#include <iostream>
#include <vector>
#include <queue>
#include <climits>using namespace std;// 定义图的邻接表表示，每个元素是一个pair，表示邻居节点和边的权值
vector<vector<pair<int, int>>> graph;// Dijkstra算法函数
void dijkstra(int start, vector<int>& dist) {int numNodes = dist.size();vector<bool> visited(numNodes, false);dist[start] = 0;priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;pq.push({0, start});while (!pq.empty()) {int currentNode = pq.top().second;pq.pop();if (visited[currentNode]) {continue; // 跳过已访问过的节点}visited[currentNode] = true;for (const pair<int, int>& neighbor : graph[currentNode]) {int neighborNode = neighbor.first;int weight = neighbor.second;if (dist[currentNode] + weight < dist[neighborNode]) {dist[neighborNode] = dist[currentNode] + weight;pq.push({dist[neighborNode], neighborNode});}}}
}int main() {int numNodes = 6;int startNode = 0;graph.resize(numNodes);vector<int> dist(numNodes, INT_MAX); // 初始化距离数组// 构建带权有向图的邻接表表示graph[0].emplace_back(1, 2);graph[0].emplace_back(2, 4);graph[1].emplace_back(2, 1);graph[1].emplace_back(3, 7);graph[2].emplace_back(3, 3);graph[3].emplace_back(4, 1);graph[4].emplace_back(5, 2);dijkstra(startNode, dist);cout << "从节点 " << startNode << " 到其他节点的最短距离：" << endl;for (int i = 0; i < numNodes; i++) {cout << "节点 " << i << ": " << dist[i] << endl;}return 0;
}

Prim 算法

最小支撑树（MST）

连通图G的某一无环连通子图T若覆盖G中所有的顶点，则称作G的一棵支撑树或生成树。

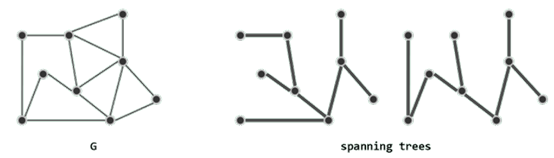
就保留原图中边的数目而言，支撑树既是“禁止环路”前提下的极大子图，也是“保持连通”前提下的最小子图。
尽管同一幅图可能有多棵支撑树，但由于其中的顶点总数均为n，故其采用的边数也均为n - 1。

若图G为一带权网络，则每一棵支撑树的成本即为其所采用各边权重的总和。在G的所有支撑树中，成本最低者称作最小支撑树（MST）。

歧义性： 尽管同一带权网络通常都有多棵支撑树，但总数毕竟有限，故必有最低的总体成本。然而，总体成本最低的支撑树却未必唯一。

蛮力算法

逐一考查G的所有支撑树并统计其成本，从而挑选出其中的最低者。然而根据Cayley公式，由n个互异顶点组成的完全图共有n^(n-2) 棵支撑树，即便忽略掉构造所有支撑树所需的成本，仅为更新最低成本的记录就需要 O(n^(n-2) 时间。

Prim 算法

Prim算法是一种用于求解最小生成树（Minimum Spanning Tree，MST）的贪心算法。最小生成树是一个连通图的子图，它包含了图中的所有节点，但只包含足够的边以保持树的性质，并且具有最小的总边权之和。Prim算法的目标是构建具有最小总边权的最小生成树。

图G = (V; E)中，顶点集V的任一非平凡子集U及其补集V\U都构成G的一个割，记作(U : V\U)。若边uv满足u∈U且 $v\notin U$，则称作该割的一条跨越边。因此类边联接于V及其补集之间，故亦形象地称作该割的一座桥。

最小支撑树总是会采用联接每一割的最短跨越边

图(a)所示假设uv是割(U : V\U)的最短跨越边，而最小支撑树T并未采用该边。于是由树的连通性，如图(b)所示在T中必有至少另一跨边st联接该割（有可能s = u或t = v，尽管二者不能同时成立）。同样由树的连通性，T中必有分别联接于u和s、v和t之间的两条通路。由于树是极大的无环图，故倘若将边uv加至T中，则如图(c )所示，必然出现穿过u、v、t 和 s的唯一环路。接下来，只要再删除边st，则该环路必然随之消失。
经过如此的一出一入，若设T转换为T'，则T'依然是连通图，且所含边数与T相同均为n - 1。这就意味着，T'也是原图的一棵支撑树。

template <typename Tv, typename Te> struct PrimPU { //针对 Prim 算法的顶点优先级更新器virtual void operator() ( Graph<Tv, Te>* g, int uk, int v ) {if ( UNDISCOVERED == g->status ( v ) ) //对亍uk每一尚未被发现的邻接顶点vif ( g->priority ( v ) > g->weight ( uk, v ) ) { //按 Prim 策略做松弛g->priority ( v ) = g->weight ( uk, v ); //更新优先级（数）g->parent ( v ) = uk; //更新父节点}}
};

顶点优先级更新器只需常数的运行时间，Prim算法的时间复杂度为O(n^2 )

实例

1.初始化一个空的最小生成树，开始时只包含一个任意选择的起始节点。
2.创建一个优先队列（最小堆），用于选择下一个要添加到最小生成树的边。将所有与初始节点相邻的边放入优先队列。
3.进入循环，直到优先队列为空：
a. 从优先队列中选择具有最小权值的边（称为最小边），并将其添加到最小生成树中。
b. 将最小边连接的节点（可能是新节点）标记为已访问。
c. 将与新节点相邻且未访问的边放入优先队列。
4.循环结束后，最小生成树就构建完成。

#include <iostream>
#include <vector>
#include <queue>
#include <climits>using namespace std;// 定义图的邻接矩阵表示，graph[i][j]表示节点i到节点j的边权值
vector<vector<int>> graph;// Prim算法函数
int prim(int numNodes) {vector<bool> visited(numNodes, false); // 标记节点是否已经访问vector<int> minEdgeWeight(numNodes, INT_MAX); // 存储每个节点到最小生成树的最小边权值int totalWeight = 0; // 最小生成树的总权值// 初始节点minEdgeWeight[0] = 0;for (int i = 0; i < numNodes; i++) {int minNode = -1;// 从未访问的节点中选择具有最小边权值的节点for (int j = 0; j < numNodes; j++) {if (!visited[j] && (minNode == -1 || minEdgeWeight[j] < minEdgeWeight[minNode])) {minNode = j;}}// 将选择的节点标记为已访问visited[minNode] = true;totalWeight += minEdgeWeight[minNode];// 更新与新节点相邻的边的权值for (int j = 0; j < numNodes; j++) {if (!visited[j] && graph[minNode][j] < minEdgeWeight[j]) {minEdgeWeight[j] = graph[minNode][j];}}}return totalWeight;
}int main() {int numNodes = 5;graph.resize(numNodes, vector<int>(numNodes, INT_MAX)); // 初始化邻接矩阵// 构建带权无向图的邻接矩阵表示graph[0][1] = 2;graph[1][0] = 2;graph[0][2] = 4;graph[2][0] = 4;graph[1][2] = 1;graph[2][1] = 1;graph[1][3] = 7;graph[3][1] = 7;graph[2][3] = 3;graph[3][2] = 3;graph[3][4] = 1;graph[4][3] = 1;int totalWeight = prim(numNodes);cout << "最小生成树的总权值为: " << totalWeight << endl;return 0;
}