目录标题
- 神经网络中的超参数
- 学习率
- 超参数优化方法
- 网格搜索法
- 随机搜索法
- 超参数搜索策略
- 粗搜索
- 精搜索
- 超参数的标尺空间
神经网络中的超参数
超参数
- 网络结构：隐层神经元个数，网络层数，非线性单元选择等
- 优化相关：学习率、dorpout比率、正则项强度等
学习率
学习率过大，训练过程无法收敛
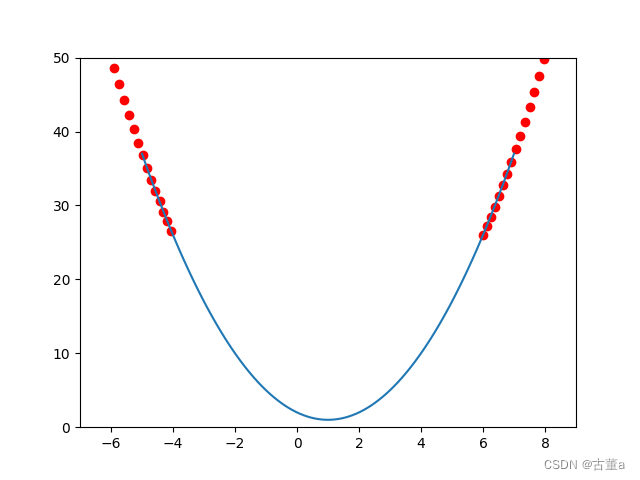
学习率偏大，在最小值附近震荡，达不到最优
学习率太小，收敛时间较长
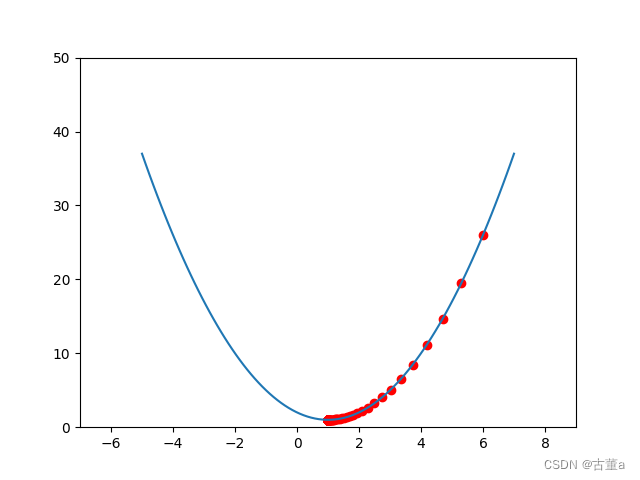
学习率适中，收敛快、结果好
超参数优化方法
网格搜索法
- 每个超参数分别取几个值，组合这些超参数值，形成多组超参数；
- 在验证集上评估每组超参数的模型性能；
- 选择性能最优的模型所采用的那组值作为最终的超参数的值。
缺点：横轴3个测试值*纵轴3个测试值=9组实验，将注意力放在了不重要的参数δ
随机搜索法
- 参数空间内随机取点，每个点对应一组超参数；
- 在验证集上评估每组超参数的模型性能；
- 选择性能最优的模型所采用的那组值作为最终的超参数的值。
优点：横轴9个测试值&纵轴9个测试值=9组实验
超参数搜索策略
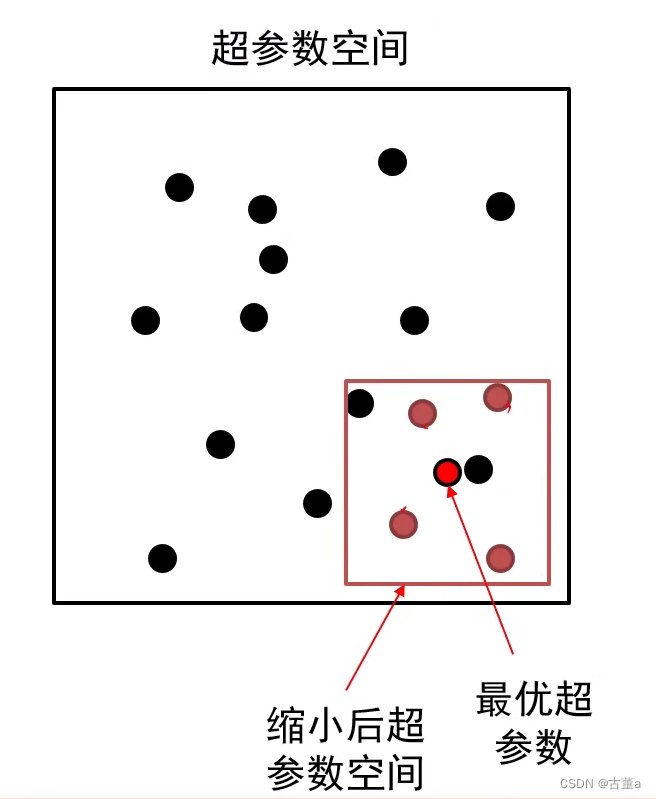
粗搜索
利用随机法在较大范围里采样超参数，训练一个周期，依据验证集正确率缩小超参数范围
精搜索
利用随机法在前述缩小的范围内采样超参数，运行模型五到十个周期，选择验证集上精度最高的那组超参数
超参数的标尺空间
例：假设最优值在0.0001到1之间，如果在0-1之间采样，90%会在0.1-1之间。
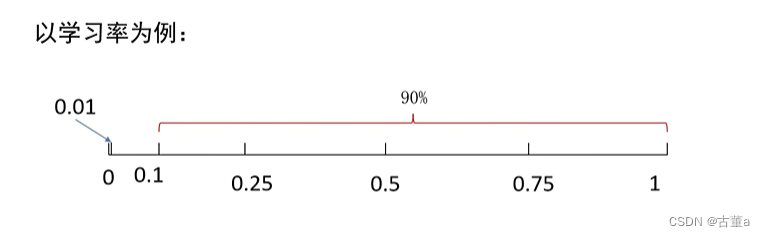
最优的值在[0.0001,1]之间，我们该如何采样？
建议：对于学习率、正则项强度这类超参数，在对数空间上进行随机采样更合适！
在1~0的量级范围内，差别不大，不敏感，所以一般在log对数空间上进行随机采样。
在log空间上，0.0001-0.001-0.01-0.1-1之间的间隔是等距的
