四、数学建模之图与网络模型

1.定义
2.例题及软件代码求解

一、定义

1.图和网络是相关概念

（1）图（Graph）：图是数学和计算机科学中的一个抽象概念，它由一组节点（顶点）和连接这些节点的边组成。图可以是有向的（有方向的，边有箭头表示方向）或无向的（没有方向的，边没有箭头表示方向）。图用于表示各种关系，如社交网络、电路、地图、组织结构等。

（2）网络（Network）：网络是一个更广泛的概念，可以包括各种不同类型的连接元素，不仅仅是图中的节点和边。网络可以包括节点、边、连接线、路由器、服务器、通信协议等多种组成部分。网络的概念在各个领域都有应用，包括计算机网络、社交网络、电力网络、交通网络等。

2.图论的概念

（1）图：图是由一组节点（顶点）和连接这些节点的边组成的数学结构。图可以分为有向图和无向图，根据边是否有方向。

（2）顶点：顶点是图中的节点，它们可以代表不同的实体或对象。

（3）边：边是连接两个顶点的线段，它可以表示顶点之间的关系或连接。

（4）有向图：有向图是一种图，其中边有方向，从一个顶点指向另一个顶点。

（5）无向图：无向图是一种图，其中边没有方向，只表示两个顶点之间的连接。

（6）最小生成树问题：在一个连通图中，寻找一个包含所有顶点的子图，使得边的权重之和最小，被称为最小生成树问题。其中，Prim算法和Kruskal算法是解决这个问题的常用方法。

（7）路径：路径是图中一系列相邻的顶点，它们通过边相连。

（8）环：环是一条路径，起始点和结束点相同，形成一个闭合的循环。

（9）连通图：如果在无向图中，任意两个顶点之间都存在路径，那么这个图是连通的。对于有向图，可以有强连通图的概念。

（10）度数：一个顶点的度数是与它相邻的边的数量。在有向图中，分为入度和出度。

（11）图的表示：图可以用邻接矩阵、邻接表等不同方式来表示，这取决于需要进行的操作和问题类型。

（12）最短路径问题：寻找两个顶点之间最短路径的问题是图论中的一个经典问题，例如Dijkstra算法和Bellman-Ford算法。

3.稀疏矩阵表示法

一种用于有效存储和处理稀疏矩阵（大部分元素为零）的方法。在很多实际应用中，矩阵中的许多元素都是零，因此使用传统的密集矩阵表示法会浪费大量的存储空间和计算资源。稀疏矩阵表示法可以显著减少这种浪费。

常见的稀疏矩阵表示法

（1）压缩稀疏行表示法：在CSR表示法中，矩阵被分为三个数组：值数组（非零元素的值）、列索引数组（每个值对应的列索引）、行偏移数组（每行的起始位置在值数组中的索引）。这种表示方法适用于稀疏矩阵中的非零元素分散地分布在各行中的情况。

（2）压缩稀疏列表示法：与CSR类似，CSC也使用值数组、行索引数组和列偏移数组，但是列偏移数组表示每列的起始位置。CSC适用于稀疏矩阵中的非零元素分散地分布在各列中的情况。

（3）三元组表示法：在这种表示法中，矩阵的每个非零元素都由一个三元组 (行号、列号、元素值) 来表示。适用于初始构建稀疏矩阵或者非常稀疏的情况，但不太适用于高效的矩阵操作。

（4）对角线存储法：当稀疏矩阵具有对角线稀疏性（非零元素主要分布在对角线上）时，可以使用对角线存储法，只存储对角线及其附近的元素。

（5）块压缩表示法：对于某些特定应用，可以将矩阵分成块，并对每个块使用一种稀疏矩阵表示法。这对于一些科学计算和图像处理任务中的大型稀疏矩阵很有用。

二、例题（matlab或lingo求解）

1.矩阵表示有向图
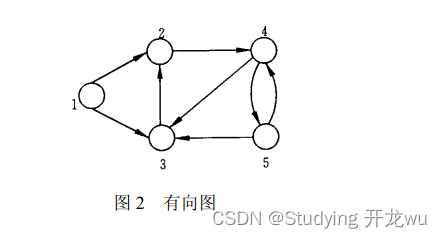
在这里插入图片描述

2.例某公司在六个城市中有分公司，从到的直接航程票价记在下述矩阵的位置上。（表示无直接航路），请帮助该公司设计一张城市到其它城市间的票价最便宜的路线图。

clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(find(a==0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb)<length(a)tb=find(pb==0);d(tb)=min(d(tb),d(temp)+a(temp,tb));tmpb=find(d(tb)==min(d(tb)));temp=tb(tmpb(1));pb(temp)=1;index1=[index1,temp];temp2=find(d(index1)==d(temp)-a(temp,index1));index2(temp)=index1(temp2(1));
end
d, index1, index2

3.例在图 3 中，用点表示城市，现有 A, B1, B2 ,C1,C2 ,C3 , D 共 7 个城市。点与
点之间的连线表示城市间有道路相连。连线旁的数字表示道路的长度。现计划从城市 A到城市 D 铺设一条天然气管道，请设计出最小价格管道铺设方案。
在这里插入图片描述
编写 LINGO 程序如下：


model: 
sets: 
cities/A,B1,B2,C1,C2,C3,D/; 
roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1, 
B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x; 
endsets 
data: 
w=2 4 3 3 1 2 3 1 1 3 4; 
enddata 
n=@size(cities); !城市的个数; 
min=@sum(roads:w*x); 
@for(cities(i)|i #ne#1 #and# i #ne#n: 
@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i))); 
@sum(roads(i,j)|i #eq#1:x(i,j))=1; 
@sum(roads(i,j)|j #eq#n:x(i,j))=1; 
end

例无向图的最短路问题）求图 4 中 1 v 到 11 v 的最短路。

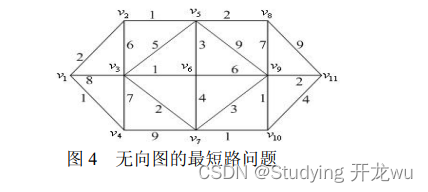
在这里插入图片描述
编写 LINGO 程序如下

：
model: 
sets: 
cities/1..11/; 
roads(cities,cities):w,x; 
endsets 
data: 
w=0; 
enddata 
calc: 
w(1,2)=2;w(1,3)=8;w(1,4)=1; 
w(2,3)=6;w(2,5)=1;
w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2; 
w(4,7)=9; 
w(5,6)=3;w(5,8)=2;w(5,9)=9; 
w(6,7)=4;w(6,9)=6; 
w(7,9)=3;w(7,10)=1; 
w(8,9)=7;w(8,11)=9; 
w(9,10)=1;w(9,11)=2;w(10,11)=4; 
@for(roads(i,j):w(i,j)=w(i,j)+w(j,i)); 
@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j))); 
endcalc 
n=@size(cities); !城市的个数; 
min=@sum(roads:w*x); 
@for(cities(i)|i #ne#1 #and# i #ne# 
n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i))); 
@sum(cities(j):x(1,j))=1; 
@sum(cities(j):x(j,1))=0; !不能回到顶点1; 
@sum(cities(j):x(j,n))=1; 
@for(roads:@bin(x)); 
end