怒刷LeetCode的第11天（Java版）

第一题

题目来源

题目内容

解决方法

方法一：迭代

方法二：递归

方法三：指针转向

第二题

题目来源

题目内容

解决方法

方法一：快慢指针

方法二：Arrays类的sort方法

方法三：计数器

方法四：额外的数组

第三题

题目来源

题目内容

解决方法

方法一：双指针

方法二：List

方法三：交换元素

方法四：递归

第一题

题目来源

25. K 个一组翻转链表 - 力扣（LeetCode）

题目内容

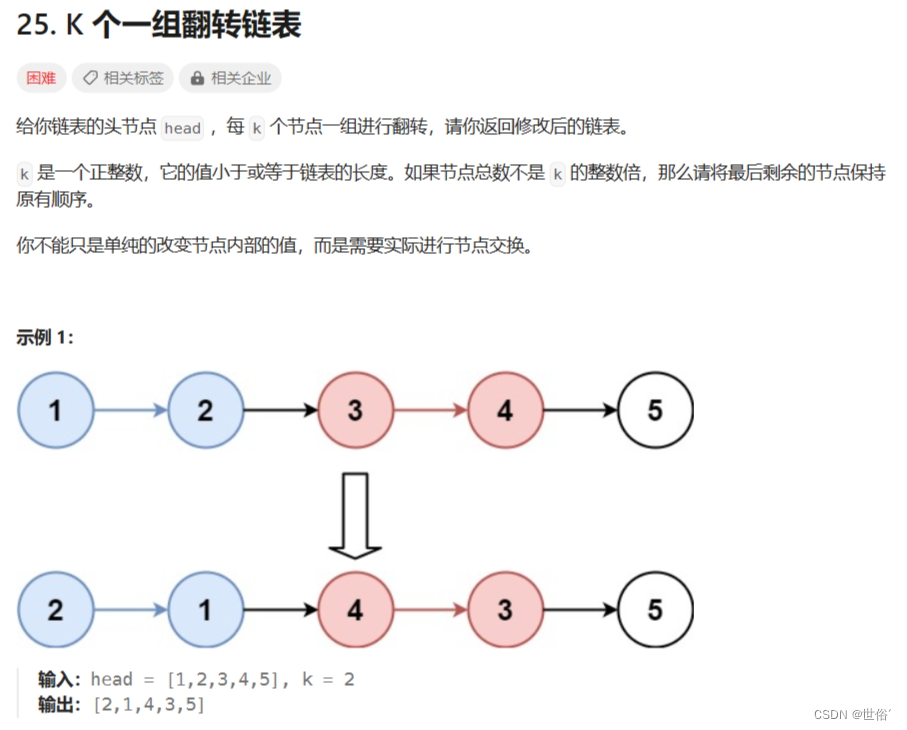
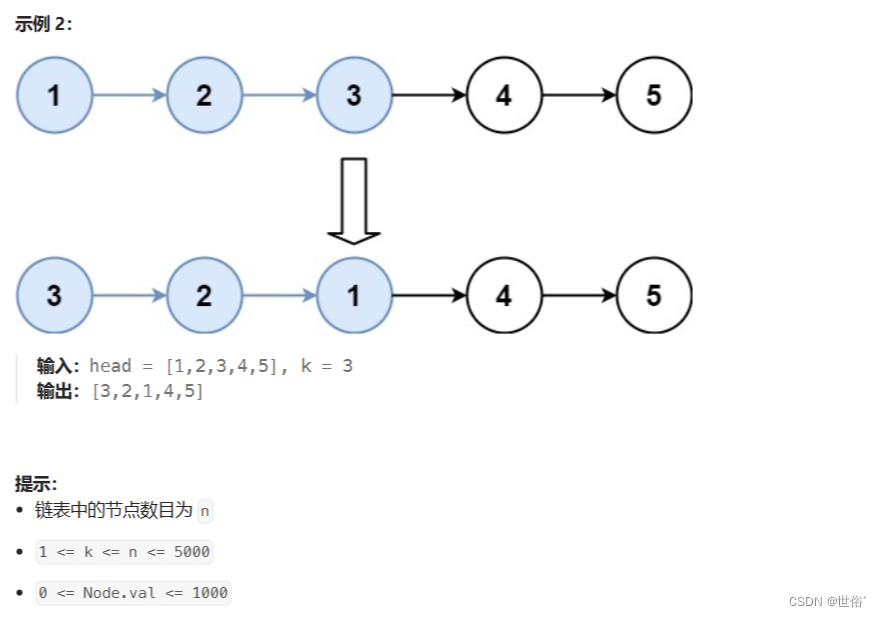
解决方法

方法一：迭代

题目描述中要求将链表每 k 个节点作为一组进行翻转。这是一个比较经典的链表问题，可以使用迭代的方法来解决。具体思路如下：

首先定义两个指针 prev 和 curr，分别指向当前组的前一个节点和当前节点。
使用一个计数器 count 来记录当前组中已经遍历的节点数目。
遍历链表，对于每个节点 curr：
- 将 curr 的下一个节点保存到 next。
- 如果 count 等于 k，则说明当前组内的节点已经遍历完毕，需要进行翻转。具体操作如下：
  - 调用 reverse 函数对 prev 和 curr 之间的节点进行翻转，返回翻转后的头节点，并将它赋值给新的 prev。
  - 将翻转后的最后一个节点的 next 指向 next，即连接下一组的头节点。
  - 更新 curr 和 prev，将它们都指向 next。
  - 将 count 重置为 0，表示下一组的遍历开始。
- 如果 count 不等于 k，则说明当前组内的节点还未满 k 个，继续遍历下一个节点。
- 将 curr 更新为 next，继续遍历下一个节点。
- 将 count 增加 1。
返回翻转后的链表头节点。

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {ListNode dummy = new ListNode(0);dummy.next = head;ListNode prev = dummy;ListNode curr = head;int count = 0;while (curr != null) {count++;ListNode next = curr.next;if (count == k) {prev = reverse(prev, next);count = 0;}curr = next;}return dummy.next;
}private ListNode reverse(ListNode start, ListNode end) {ListNode prev = start;ListNode curr = start.next;ListNode first = curr;while (curr != end) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}start.next = prev;first.next = curr;return first;
}}

复杂度分析：

时间复杂度分析：

遍历链表需要 O(n) 的时间，其中 n 是链表的长度。
在每个节点组内进行翻转操作时，需要遍历 k 个节点，即 O(k) 的时间复杂度。
总共有 n/k 个节点组，所以翻转操作的总时间复杂度是 O((n/k) * k) = O(n)。

因此，总的时间复杂度是 O(n)。

空间复杂度分析：

我们只使用了常数级别的额外空间，例如指针变量和辅助节点。
因此，空间复杂度是 O(1)。

综上所述，该解法的时间复杂度为 O(n)，空间复杂度为 O(1)。

LeetCode运行结果：

方法二：递归

除了迭代的解法，还可以使用递归的思路来实现链表的翻转。

具体的递归思路如下：

定义一个函数 reverseKGroupRecursive，其功能是将以 head 为头节点的链表每 k 个节点进行翻转，并返回翻转后的链表的头节点。
首先遍历链表，找到第 k+1 个节点 next。
- 如果 next!=null，说明当前组内有至少 k 个节点，可以进行翻转操作。
  - 调用 reverse 函数对以 head 为头节点、以 next 为尾节点的子链表进行翻转，并将翻转后的尾节点返回，将其赋值给 newHead。
  - 将 head 的 next 指针指向下一组的头节点，即调用 reverseKGroupRecursive(next, k)。
  - 返回 newHead，作为翻转后的链表的头节点。
- 如果 next==null，说明剩余的节点数少于 k 个，无需翻转，直接返回 head。

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {ListNode curr = head;int count = 0;while (curr != null && count < k) {curr = curr.next;count++;}if (count == k) {ListNode newHead = reverseKGroupRecursive(head, curr, k);head.next = reverseKGroup(curr, k);return newHead;}return head;
}private ListNode reverseKGroupRecursive(ListNode head, ListNode tail, int k) {ListNode prev = tail;ListNode curr = head;while (curr != tail) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}return prev;
}}

复杂度分析：

时间复杂度分析：

遍历链表需要 O(n) 的时间，其中 n 是链表的长度。
递归调用了 n/k 次，每次都需要翻转 k 个节点，因此每次递归操作的时间复杂度是 O(k)。
整个算法的时间复杂度是 O((n/k) * k) = O(n)。

因此，总的时间复杂度是 O(n)。

空间复杂度分析：

递归的深度是 n/k，因此递归调用栈的最大深度是 O(n/k)。
每次递归操作需要常数级别的额外空间，例如指针变量和辅助节点。
因此，空间复杂度是 O(n/k)，在最坏情况下为 O(n)。需要注意的是，在实际使用中链表长度较大时，递归方法可能会导致递归调用栈溢出。

综上所述，递归解法的时间复杂度为 O(n)，空间复杂度为 O(n/k)（在最坏情况下为 O(n)）。

需要注意的是，递归方法对于链表长度较大时可能会导致递归调用栈溢出，因此在实际使用中需要注意链表长度是否适合使用递归解法。

LeetCode运行结果：

方法三：指针转向

除了迭代、递归的方法，还可以使用指针转向的思路来实现链表的翻转。

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
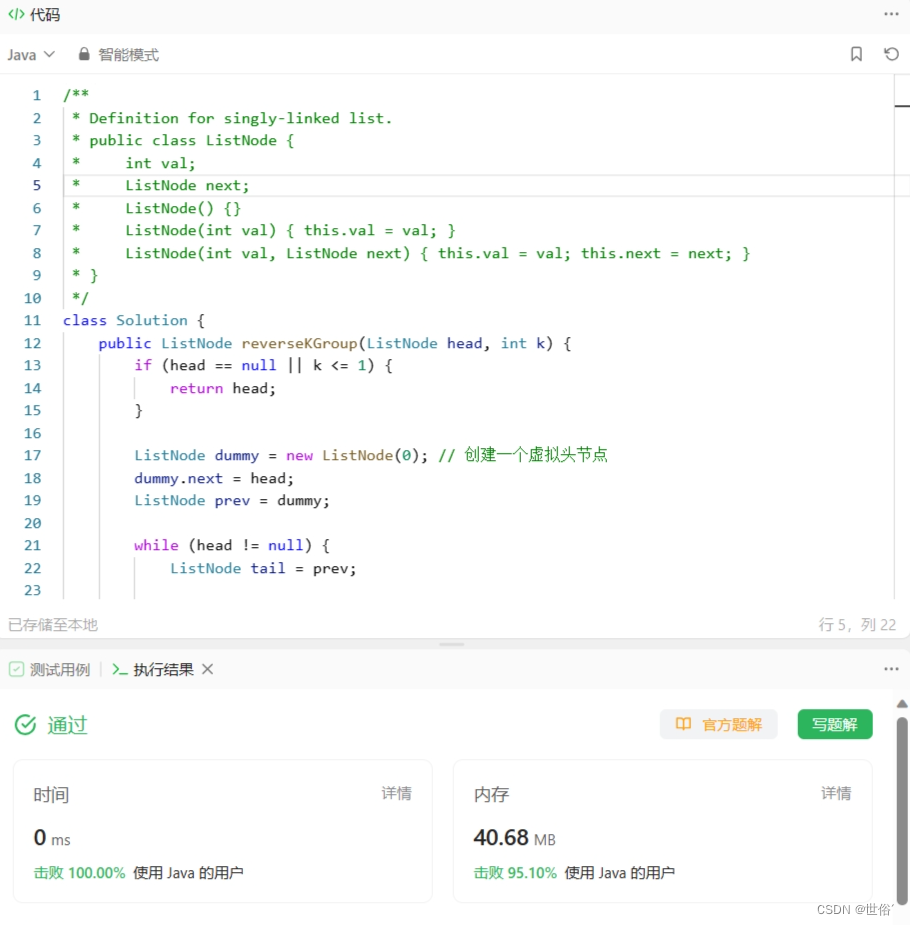
class Solution {public ListNode reverseKGroup(ListNode head, int k) {if (head == null || k <= 1) {return head;}ListNode dummy = new ListNode(0); // 创建一个虚拟头节点dummy.next = head;ListNode prev = dummy;while (head != null) {ListNode tail = prev;// 判断剩余节点数是否大于等于 kfor (int i = 0; i < k; i++) {tail = tail.next;if (tail == null) {// 剩余的节点数不满 k 个，直接返回结果return dummy.next;}}ListNode nextGroupHead = tail.next; // 下一组节点的头节点// 翻转当前组内的节点ListNode[] reversed = reverse(head, tail);head = reversed[0];tail = reversed[1];// 将翻转后的组连接到结果链表中prev.next = head;tail.next = nextGroupHead;// 更新 prev 和 head，准备处理下一组prev = tail;head = nextGroupHead;}return dummy.next;}private ListNode[] reverse(ListNode head, ListNode tail) {ListNode prev = tail.next;ListNode curr = head;while (prev != tail) {ListNode next = curr.next;curr.next = prev;prev = curr;curr = next;}return new ListNode[] {tail, head};}
}

该方法通过指针转向的方式，每次翻转一组的节点。其中，reverse 方法用于翻转当前组内的节点。

复杂度分析：

时间复杂度分析：

翻转一组的时间复杂度为 O(k)，其中 k 是每组节点的数量。
对于包含 n 个节点的链表，一共有 n/k 组需要翻转。
因此，总的时间复杂度为 O((n/k) * k) = O(n)。

空间复杂度分析：

空间复杂度取决于额外使用的变量和递归调用栈的空间。
额外使用的变量有 dummy、prev、tail 和 nextGroupHead，它们占用的空间是常数级别的，因此不会随着输入规模 n 的增加而增加。
在递归实现中，递归调用栈的深度最多为 n/k，因为总共有 n/k 组需要翻转。
因此，递归调用栈的空间复杂度为 O(n/k)。
综上所述，总的空间复杂度为 O(1)。

综合来说，该方法的时间复杂度为 O(n)，空间复杂度为 O(1)。需要注意的是，在处理不满 k 个节点的情况时，需要额外判断并返回结果。

LeetCode运行结果：

第二题

题目来源

26. 删除有序数组中的重复项 - 力扣（LeetCode）

题目内容

解决方法

方法一：快慢指针

由于数组已经按非严格递增排列，可以利用快慢指针来遍历数组。慢指针指向当前不重复的元素，快指针用于遍历整个数组。如果快指针指向的元素与慢指针指向的元素不同，说明找到了一个新的不重复元素，将其存放在慢指针的下一个位置，并将慢指针后移一位。最后返回慢指针加1即可。

class Solution {
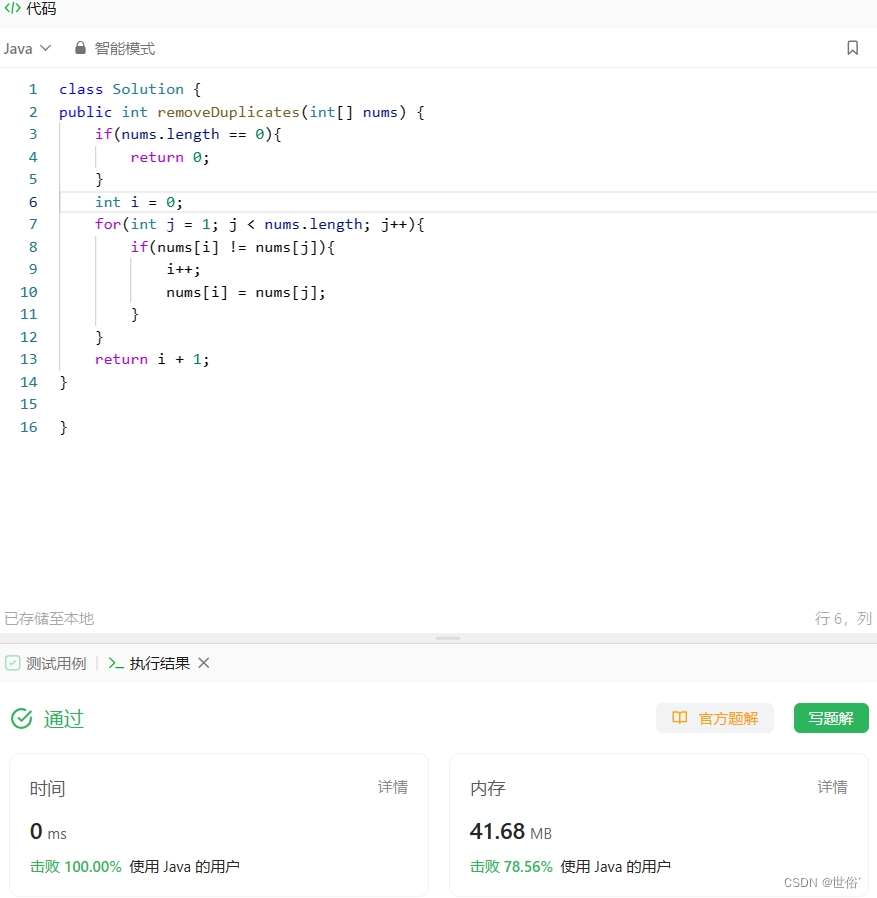
public int removeDuplicates(int[] nums) {if(nums.length == 0){return 0;}int i = 0;for(int j = 1; j < nums.length; j++){if(nums[i] != nums[j]){i++;nums[i] = nums[j];}}return i + 1;
}}

复杂度分析：

时间复杂度：O(n)，其中n为数组的长度。该算法通过使用快慢指针，只需一次遍历数组即可完成操作。
空间复杂度：O(1)。该算法只使用了常数级的额外空间，不随输入规模的增加而增加。

LeetCode运行结果：

方法二：Arrays类的sort方法

除了使用快慢指针的解法外，在Java中还可以使用Arrays类的sort方法来解决该问题。

该方法首先对数组进行排序，使得重复元素相邻。然后使用快慢指针的方法遍历数组，将不重复的元素放到慢指针所指向的位置，并移动慢指针。最后返回慢指针加1作为新数组的长度。

class Solution {
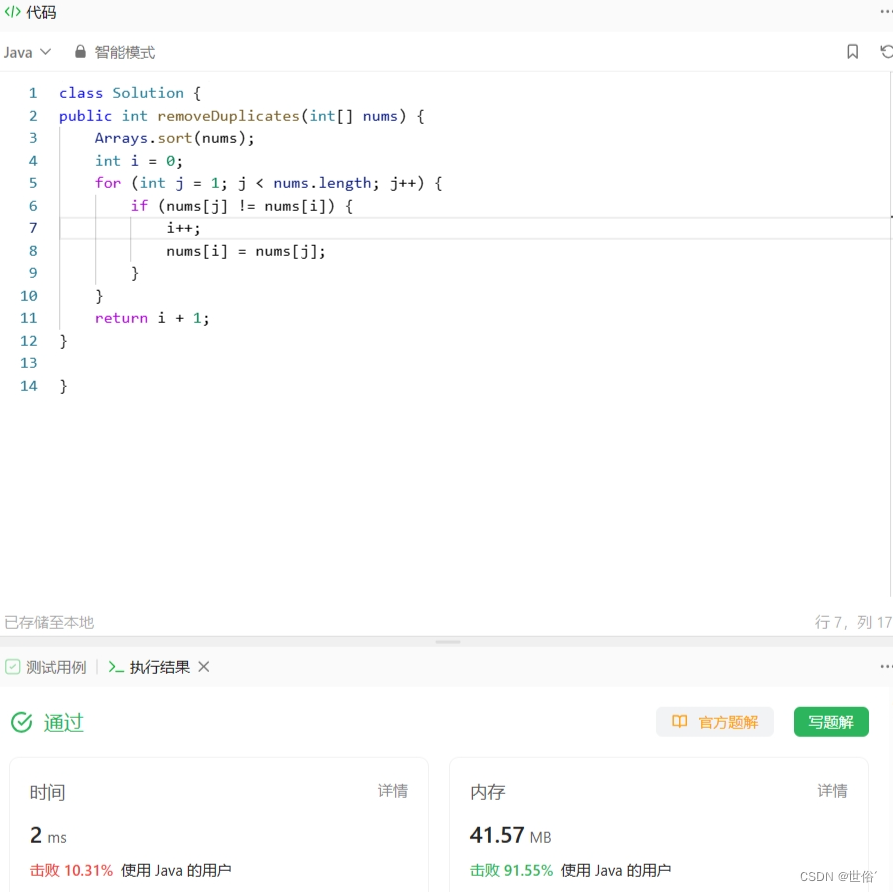
public int removeDuplicates(int[] nums) {Arrays.sort(nums);int i = 0;for (int j = 1; j < nums.length; j++) {if (nums[j] != nums[i]) {i++;nums[i] = nums[j];}}return i + 1;
}}

复杂度分析：

时间复杂度：O(n log n)，其中n为数组的长度。排序需要O(n log n)的时间复杂度，遍历数组需要O(n)的时间复杂度。
空间复杂度：O(1)，原地修改数组，不需要额外的空间。

LeetCode运行结果：

方法三：计数器

除了前面提到的思路和方法，还可以使用一个计数器来记录重复元素的个数，并根据计数器的值进行相应的操作。

该方法使用count变量来记录数组中不重复元素的个数，duplicateCount变量来记录重复元素的个数。
遍历数组时，如果当前元素与前一个元素相同，则将duplicateCount加1；否则将count加1。
同时，如果duplicateCount大于0，则将当前元素向前移动duplicateCount个位置，相当于删除了重复元素。
最后返回count作为新数组的长度。

class Solution {
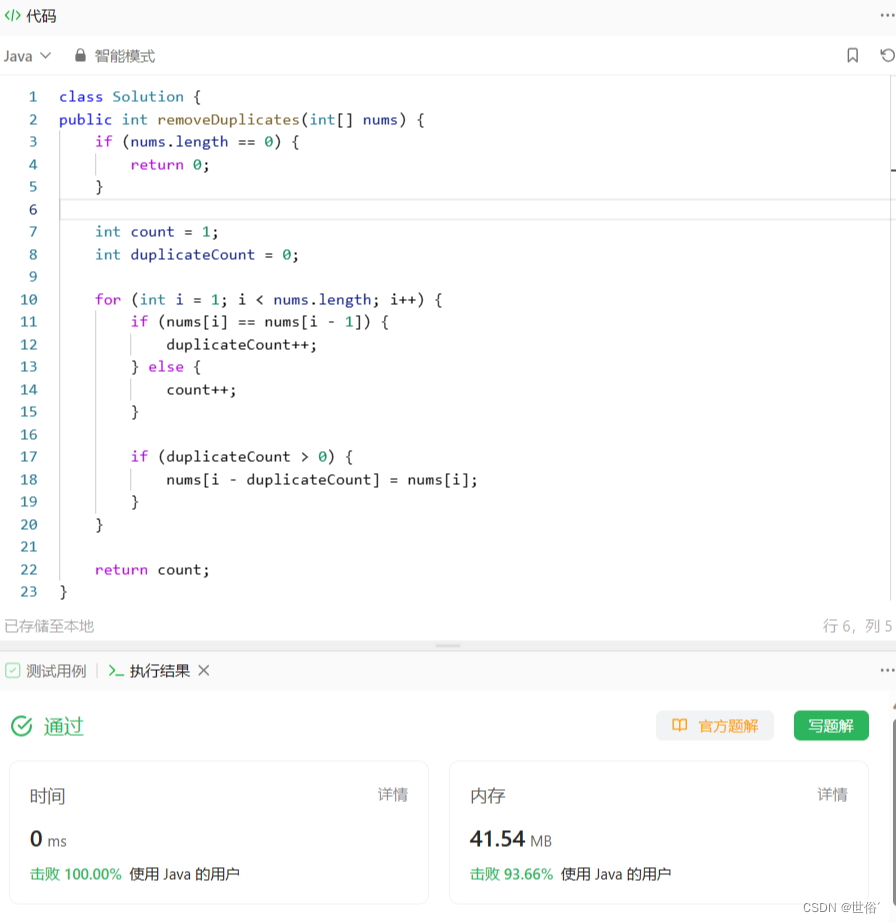
public int removeDuplicates(int[] nums) {if (nums.length == 0) {return 0;}int count = 1;int duplicateCount = 0;for (int i = 1; i < nums.length; i++) {if (nums[i] == nums[i - 1]) {duplicateCount++;} else {count++;}if (duplicateCount > 0) {nums[i - duplicateCount] = nums[i];}}return count;
}}

复杂度分析：

时间复杂度：O(n)，其中n为数组的长度。需要遍历整个数组一次。
空间复杂度：O(1)，原地修改数组，不需要额外的空间。

在遍历数组时，只有在出现重复元素时才会对数组进行修改。对数组的修改是通过将重复元素向前移动来实现的，而不是删除重复元素。因此，不需要额外的空间来存储删除后的新数组。这种方法的空间复杂度是常数级别的。

综上所述，使用计数器的解法是一种高效的解决方案，具有线性的时间复杂度和常数级别的空间复杂度。

LeetCode运行结果：

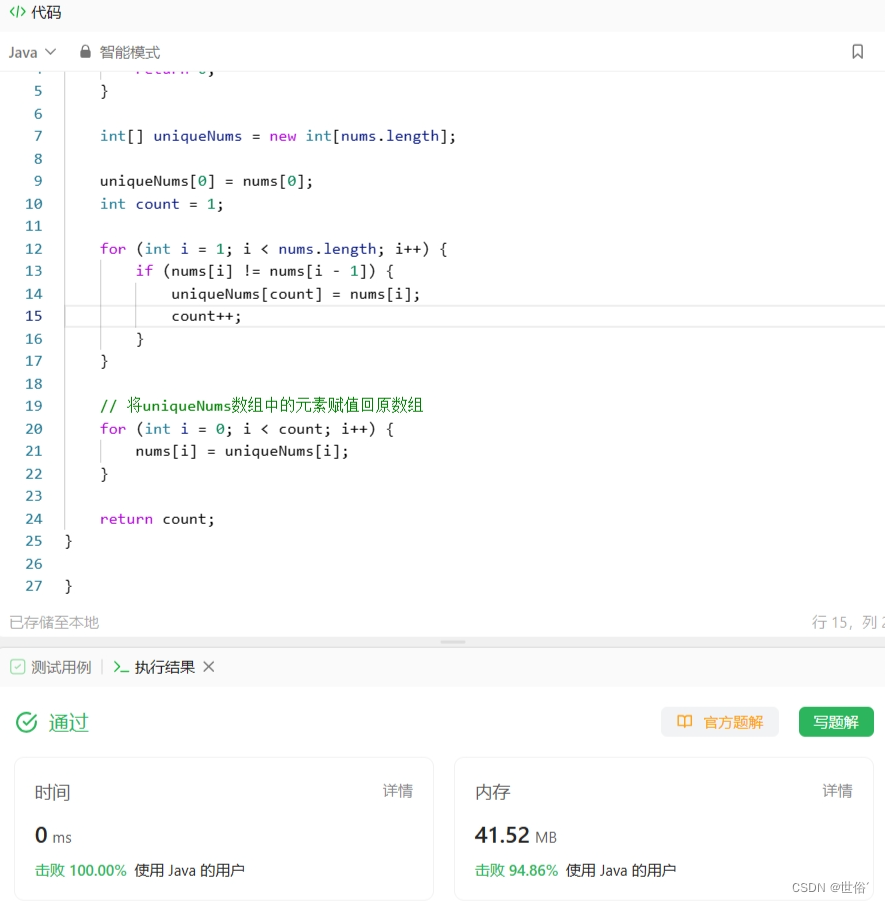
方法四：额外的数组

除了之前提到的思路和方法，还可以使用额外的数组来存储不重复的元素。

该方法创建一个新的数组uniqueNums，用于存储不重复的元素。遍历原始数组时，如果当前元素与前一个元素不相同，则将当前元素添加到uniqueNums数组中，并将计数器count加1。最后，将uniqueNums数组中的元素赋值回原数组nums，并返回count作为新数组的长度。

class Solution {
public int removeDuplicates(int[] nums) {if (nums.length == 0) {return 0;}int[] uniqueNums = new int[nums.length];uniqueNums[0] = nums[0];int count = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] != nums[i - 1]) {uniqueNums[count] = nums[i];count++;}}// 将uniqueNums数组中的元素赋值回原数组for (int i = 0; i < count; i++) {nums[i] = uniqueNums[i];}return count;
}}

复杂度分析：

时间复杂度：O(n)，其中n为数组的长度。需要遍历整个数组一次，并进行一次数组元素的复制操作。
空间复杂度：O(n)，因为需要使用额外的数组来存储不重复的元素。

在遍历原始数组时，只有在出现与前一个元素不相同的元素时才将其添加到新数组中。因此，新数组的长度最多为原数组的长度，即使用了额外的O(n)空间。

综上所述，使用额外数组的解法是一种线性时间复杂度的解决方案，但需要额外的空间来存储新的数组。这种方法适用于不要求原地修改数组的情况。

LeetCode运行结果：

第三题

题目来源

27. 移除元素 - 力扣（LeetCode）

题目内容

解决方法

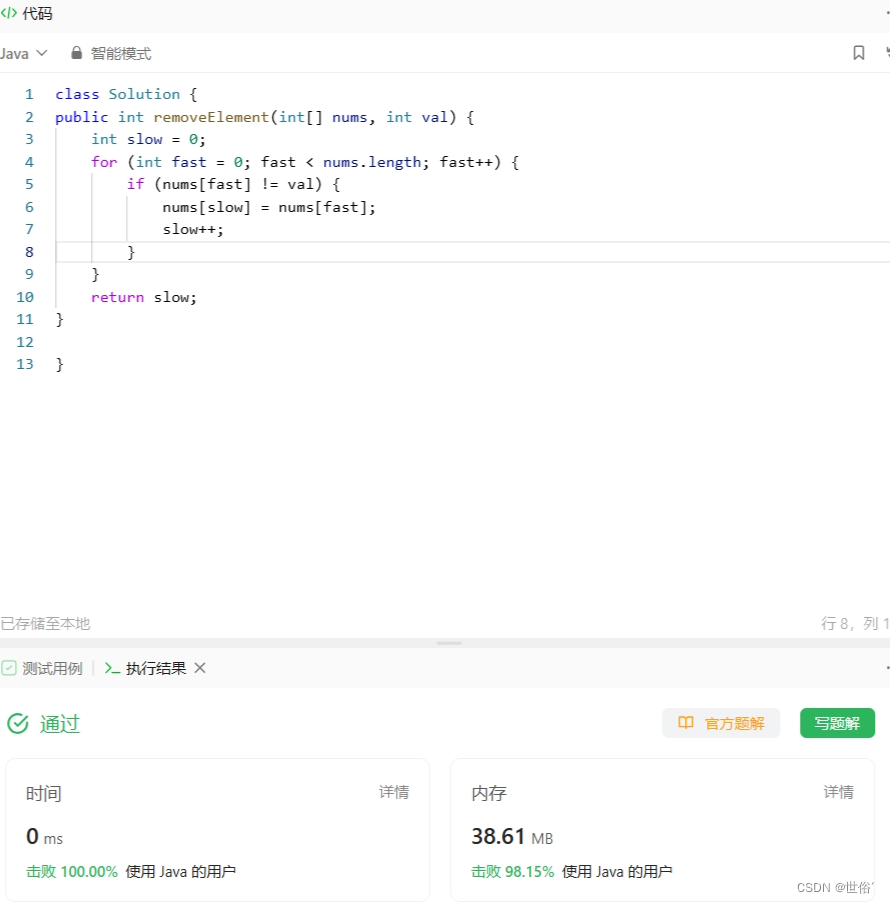
方法一：双指针

这道题可以使用双指针的方法来解决。定义两个指针：慢指针slow和快指针fast。

算法的思路如下：

初始化慢指针slow为0。
遍历数组，如果当前元素nums[fast]等于给定值val，则快指针fast向前移动一步，跳过该元素。
如果当前元素nums[fast]不等于给定值val，则将nums[fast]赋值给nums[slow]，同时慢指针slow向前移动一步。
重复步骤2和步骤3，直到快指针fast遍历完整个数组。
返回慢指针slow的值。

class Solution {
public int removeElement(int[] nums, int val) {int slow = 0;for (int fast = 0; fast < nums.length; fast++) {if (nums[fast] != val) {nums[slow] = nums[fast];slow++;}}return slow;
}}

复杂度分析：

时间复杂度：遍历数组所需的时间为 O(n)，其中 n 是数组的长度。在每次遍历时，只有快指针需要移动，而慢指针最多移动了 n 次。因此，整个算法的时间复杂度为 O(n)。
空间复杂度：该算法使用了常数个额外变量，不随输入规模 n 变化，因此空间复杂度为 O(1)。无论输入数组的长度如何，算法都只需要固定的额外空间。

综上所述，该算法的时间复杂度为 O(n)，空间复杂度为 O(1)。

LeetCode运行结果：

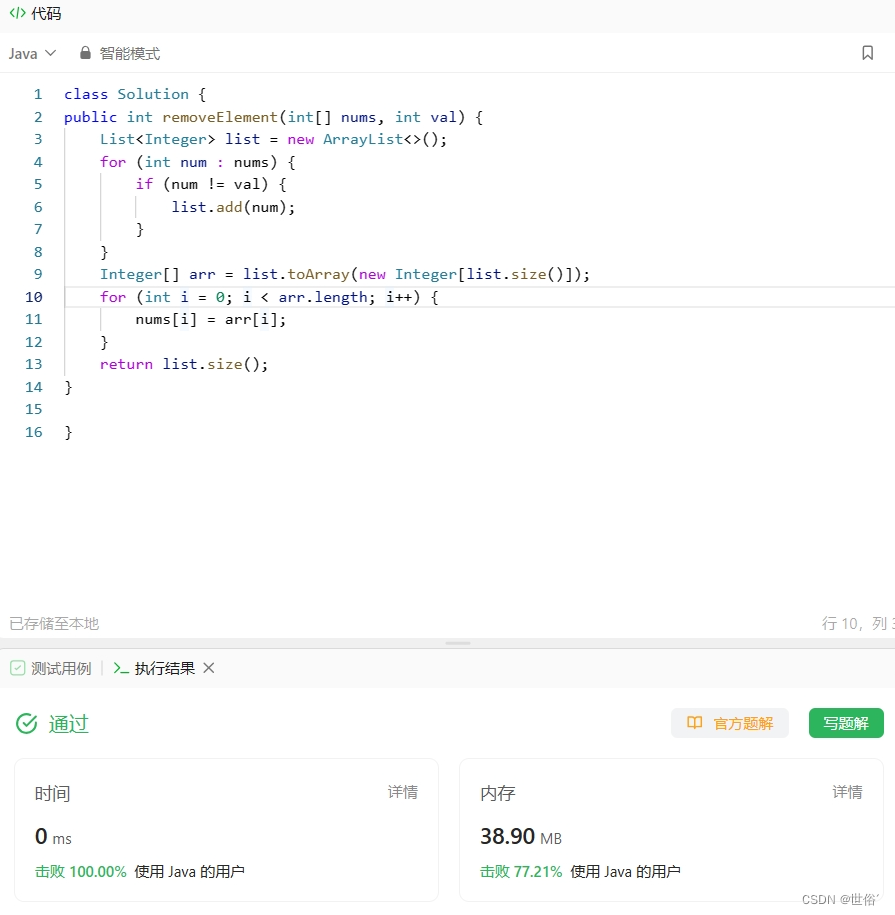
方法二：List

除了双指针的方法，还可以使用 Java 中的 List 来解决这个问题。具体的做法如下：

创建一个 List 集合（例如 ArrayList）来存储不等于给定值val的元素。
遍历数组，如果当前元素nums[i]不等于给定值val，则将其添加到 List 中。
将 List 转换为数组并返回。

class Solution {
public int removeElement(int[] nums, int val) {List<Integer> list = new ArrayList<>();for (int num : nums) {if (num != val) {list.add(num);}}Integer[] arr = list.toArray(new Integer[list.size()]);for (int i = 0; i < arr.length; i++) {nums[i] = arr[i];}return list.size();
}}

这种方法的本质是通过使用 List 集合来存储不等于给定值val的元素，然后将 List 转换为数组并重新赋值给原数组。最后返回 List 的大小即为移除元素后的新长度。

复杂度分析：

时间复杂度：

遍历数组并将不等于给定值val的元素添加到 List，时间复杂度为 O(n)，其中 n 是数组的长度。
将 List 转换为数组，需要遍历 List 中的元素，时间复杂度同样为 O(n)。

综上所述，整个算法的时间复杂度为 O(n)。

空间复杂度：

创建了一个大小为 n 的 List 来存储不等于给定值val的元素，占用了额外的 O(n) 空间。
将 List 转换为数组时，需要创建一个新的数组，大小为 List 的大小，同样占用了额外的 O(n) 空间。

综上所述，整个算法的空间复杂度为 O(n)。

相比之下，双指针和的方法在空间复杂度上是优于使用 List 的方法的，因为它只需要常数个额外变量，即空间复杂度为 O(1)。因此，建议使用双指针的方法来解决这个问题，以获得更好的空间效率。

LeetCode运行结果：

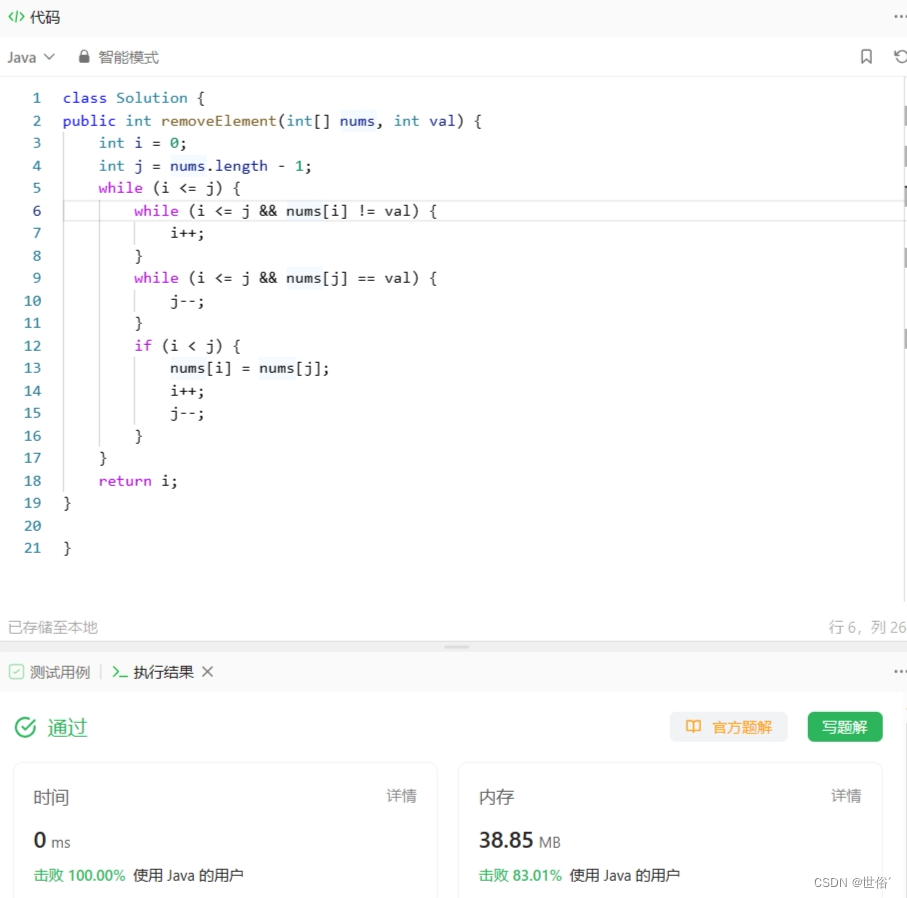
方法三：交换元素

除了双指针、List，还可以使用交换元素的思路来解决这个问题。具体的做法如下：

初始化两个指针i和j，初始值分别为0和数组长度-1。
循环移动指针i，直到找到第一个等于给定值val的元素。
循环移动指针j，直到找到第一个不等于给定值val的元素。
如果i小于j，则将元素nums[j]赋值给nums[i]，并将指针i和j分别加1和减1。
重复步骤2到步骤4，直到i大于等于j。
返回指针i，即为移除元素后的新长度。

class Solution {
public int removeElement(int[] nums, int val) {int i = 0;int j = nums.length - 1;while (i <= j) {while (i <= j && nums[i] != val) {i++;}while (i <= j && nums[j] == val) {j--;}if (i < j) {nums[i] = nums[j];i++;j--;}}return i;
}}

这种交换元素的方法通过使用两个指针分别从头尾向中间移动，并通过交换元素的方式来实现移除元素的目的。

复杂度分析：

时间复杂度：使用两个指针分别从头尾向中间移动，最坏情况下需要遍历整个数组，时间复杂度为 O(n)，其中 n 是数组的长度。
空间复杂度：这种方法只使用常数个额外变量，即空间复杂度为 O(1)。

综上所述，使用交换元素的方法的时间复杂度为 O(n)，空间复杂度为 O(1)。与双指针的方法相比，交换元素的方法具有相同的时间复杂度，但空间复杂度更低，因为不需要额外的数据结构（如 List）来存储元素。从空间效率的角度来看，交换元素的方法是较优的选择。

LeetCode运行结果：

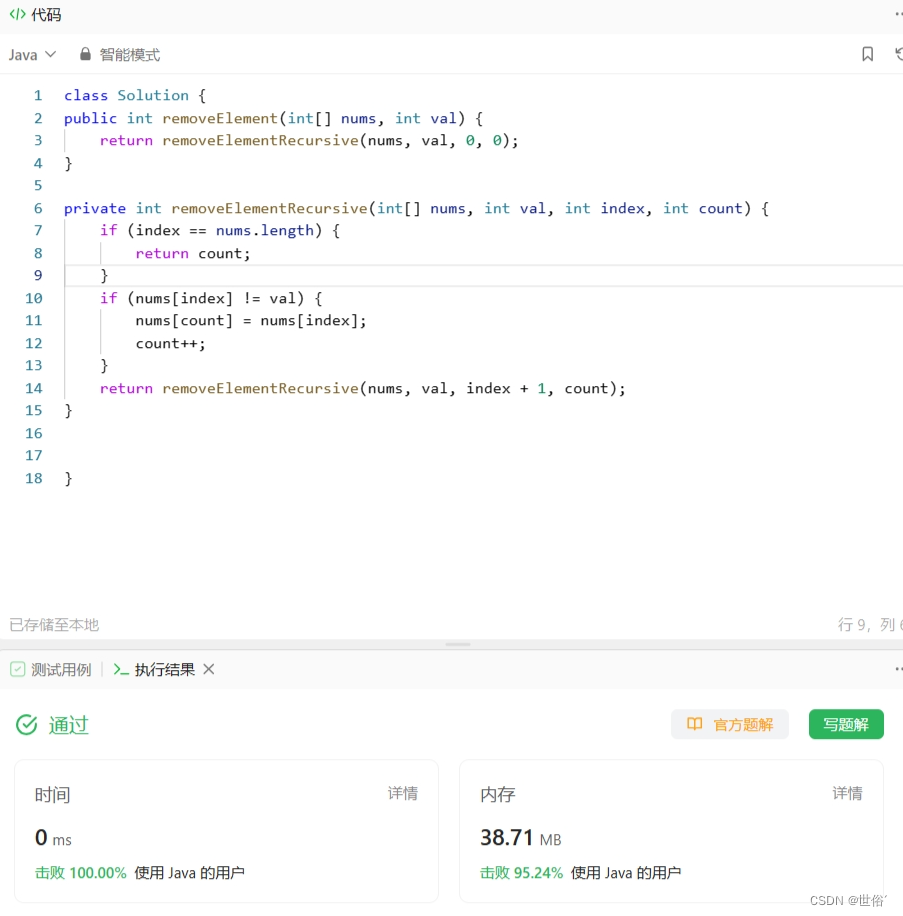
方法四：递归

除了双指针、交换元素和使用 List 的方法，还可以利用递归来解决这个问题。具体的做法如下：

编写一个递归函数，传入当前遍历到的索引位置和计数器 count。
在递归函数中，判断当前遍历到的元素是否等于给定值 val：
- 如果相等，则将计数器 count 加1，并调用递归函数继续处理下一个元素。
- 如果不相等，则将当前元素覆盖掉索引位置 count，并调用递归函数处理下一个元素。
递归函数的终止条件是遍历完整个数组，返回计数器 count 的值。
在主函数中，调用递归函数，传入初始索引0和计数器初始值0。

class Solution {
public int removeElement(int[] nums, int val) {return removeElementRecursive(nums, val, 0, 0);
}private int removeElementRecursive(int[] nums, int val, int index, int count) {if (index == nums.length) {return count;}if (nums[index] != val) {nums[count] = nums[index];count++;}return removeElementRecursive(nums, val, index + 1, count);
}}

这种递归的方法通过逐个处理数组元素，将不等于给定值 val 的元素覆盖到数组的前部分，从而实现移除元素的目的。

复杂度分析：