目录
- 一、排序算法总结
- (一)排序算法分类
- (二)表格比较
- 二、详细分析(最重要考点!!!)
- (一)稳定性
- (二)时间复杂度
- (三)空间复杂度
- (四)比较次数
- (五)平均比较次数
- (六)排序趟数
- (七)根据规模选择排序算法
- (八)每趟确定的元素最终位置
- (九)存储方式的选择
一、排序算法总结
常用排序算法如下:
(一)排序算法分类
根据所要排序的元素是否完全在内存中进行排序,可分为以下两种:
| 名称 | 特点 |
|---|---|
| 内部排序(In-place) | 排序的元素完全在内存中 |
| 外部排序(Out-place) | 在排序过程中不断在内、外存之间交换 |
其中归并排序、基数排序是外部排序,其它均为内部排序。
(二)表格比较
共五大类九种排序算法,插入类可分为直接插入、折半插入和希尔排序,交换类可分为冒泡排序和快速排序,选择类可分为简单选择和堆排序,以及剩下的归并排序与基数排序。
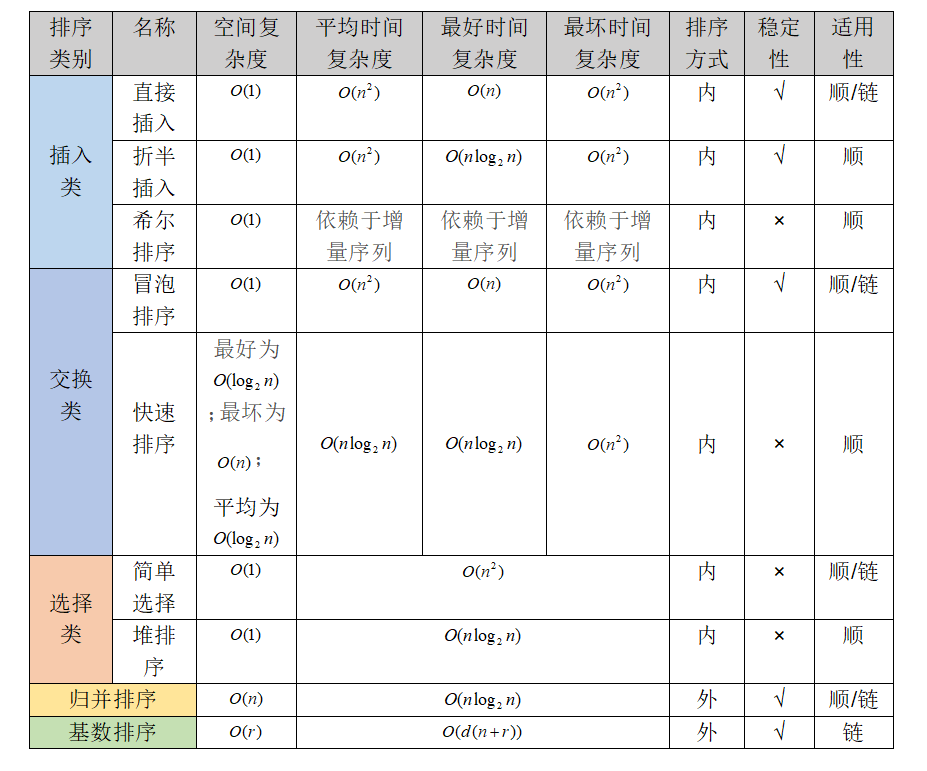
二、详细分析(最重要考点!!!)
(一)稳定性
- 插入排序(直接/折半)、冒泡排序、归并排序和基数排序是
稳定的排序算法,其中平均时间复杂度为O(nlog2n)的稳定排序只有归并排序。
- 对于
插入、交换、选择三大类的排序算法,较简单型的排序算法一般都是稳定的(除了希尔排序、快速排序、简单选择排序)。 较复杂型的排序算法都是不稳定的,排序中元素的相对位置会发生变化,例如希尔排序、快速排序、堆排序,另外,还有简单选择排序。
(二)时间复杂度
- 由于直接/折半插入排序、简单选择排序、冒泡排序是
较简单型的排序算法,其算法实现过程较简单,时间复杂度均为O(n2),但在最好情况下折半插入排序可以达到O(nlog2n),直接插入排序和冒泡排序可以达到O(n),但简单选择排序中元素的比较次数与序列的初始状态无关,所以其时间复杂度始终为O(n2);另外,这四种较简单型的排序算法的空间复杂度均为O(1)。
| 排序算法 | 空间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 |
|---|---|---|---|---|
| 直接插入排序 | O(1) | O(n2) | O(n) | O(n2) |
| 折半插入排序 | O(1) | O(n2) | O(nlog2n) | O(n2) |
| 冒泡排序 | O(1) | O(n2) | O(n) | O(n2) |
| 简单选择排序 | O(1) | O(n2) | O(n2) | O(n2) |
希尔排序也称为缩小增量排序,它属于插入类算法,是插入排序的拓展,由于时间复杂度上有较大的改进,所以对较大规模的排序可以达到很高的效率,但无法得出较精确的渐进时间;希尔排序的空间复杂度也为O(1)。
| 排序算法 | 空间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 |
|---|---|---|---|---|
| 希尔排序 | O(1) | 依赖于增量序列 | 依赖于增量序列 | 依赖于增量序列 |
- 快速排序、堆排序和归并排序是
改进型的排序算法,其平均时间复杂度均为O(nlog2n),快速排序和归并排序都采用分治的思想,而堆排序是通过使用堆这种数据结构。
| 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 |
|---|---|---|---|
| 快速排序 | O(nlog2n) | O(nlog2n) | O(n2) |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) |
- 当
快速排序的初始序列为有序或逆序时,为最坏情况,时间复杂度会达到O(n2),而初始序列越接近无序或基本上无序时,为最好情况,即时间复杂度为O(nlog2n);归并排序中,比较次数与初始序列无关,即分割子序列与初始序列是无关的;堆排序中初始建堆的时间复杂度为O(n),每下坠一层最多只需对比元素两次,每一趟不超过O(h)=O(log2n),所以归并排序和堆排序的最好、最坏时间复杂度都为O(nlog2n) 。
(三)空间复杂度
快速排序中需借助栈来进行递归,其空间复杂度与递归层数(栈的深度)有关,最坏情况下二叉树为最大高度,为n层,即最大递归深度,空间复杂度为O(n),最好情况下二叉树为最小高度,为⌊ log2n ⌋,即最小递归深度,空间复杂度为O(log2n),堆排序只需借助常数个辅助空间,空间复杂度为O(1) ,归并排序中也用到了栈,其递归工作栈的空间复杂度为O(log2n),由于另外还需用到辅助数组,其空间复杂度为O(n),所以该排序算法的空间复杂度为O(n)。
| 排序算法 | 空间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 |
|---|---|---|---|---|
| 快速排序 | 最好为O(log2n);最坏为O(n);平均情况下,为O(log2n) | O(nlog2n) | O(nlog2n) | O(n2) |
| 堆排序 | O(1) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
| 归并排序 | O(n) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
(四)比较次数
二路归并排序、简单选择排序、基数排序的比较次数都与初始序列的状态无关。
(五)平均比较次数
- 在插入排序、希尔排序、选择排序、快速排序、堆排序、归并排序和基数排序中,
平均比较次数最少的排序是快速排序。
- 直接插入排序和简单选择排序对比:通常情况下,直接插入排序每趟插入都需向后一次挪位,而简单选择排序只需找到最小/最大元素与其交换位置即可,它的移动次数较少。
考虑在较极端情况下,对于有序数组,直接插入排序的比较次数为n-1;而简单选择排序的比较次数始终为n(n-1)/2。
(六)排序趟数
- 直接插入排序、简单选择排序和基数排序的排序趟数
与初始序列无关。
(1)直接插入排序由于每趟都插入一个元素至已排好的子序列,所以排序趟数固定为n-1次;
(2)简单选择排序中,每趟排序都选出一个最小/最大的元素,所以排序趟数也固定为n-1次;
(3)基数排序需进行d趟分配和收集操作。
(七)根据规模选择排序算法
- 一般来说,对于要排序元素较多的序列,可以选用时间复杂度为O(nlog2n)的堆排序、快速排序和归并排序算法,其中
快速排序是目前基于比较的内部排序中最好的排序算法,但它要求初始序列随机分布这样才会使快速排序的平均时间最短。堆排序的空间复杂度小于快速排序,它不会出现快速排序中的最坏情况。前两种排序算法都是不稳定的,因此若要选择时间复杂度为O(nlog2n)且稳定的排序算法,即可以选择归并排序,通过将该算法与直接插入排序结合起来,即通过直接插入排序求得有序子序列后,再合并,这样的归并算法依旧是稳定的。
- 若要排序元素很大,记录的元素位数较少时,应选用
基数排序,它适用于以下:
1、数据元素的关键字可以很容易地进行拆分成d组,且d较小;
2、每组关键字的取值范围不大,即r较小;
3、数据元素个数n较大。
- 对于排序元素个数较少的序列,可以选用时间复杂度为O(n2)的直接/折半插入排序、冒泡排序、简单选择排序算法,由于
简单选择排序的移动次数比直接插入排序少,所以当元素信息量较大时,应选用简单选择排序。
(八)每趟确定的元素最终位置
每一趟排序算法的进行都能确定一个元素处于其最终位置的排序算法有以下:
①冒泡排序
②简单选择排序
③堆排序
④快速排序前三者能形成整体有序的子序列,而快速排序只确定枢轴元素的最终位置
(第n趟快速排序完成时,会有n个以上的元素处于其最终结果位置上,
即它们两边的元素分别比它大或小)。
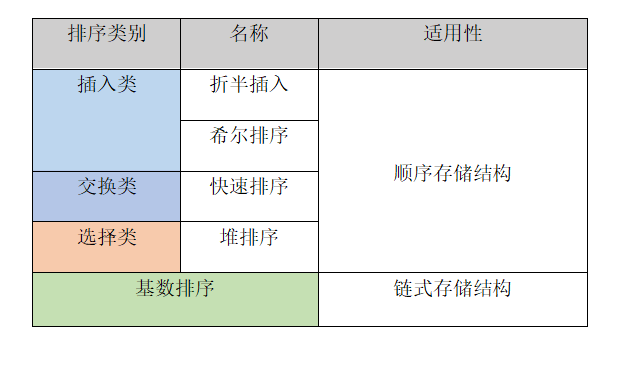
(九)存储方式的选择
- 插入类只有
折半插入和希尔排序、交换类只有快速排序、选择类只有堆排序都只适用于顺序存储,而基数排序只适用于链式存储,其他排序算法都可以支持顺序存储和链式存储,例如直接插入、冒泡排序、简单选择排序和归并排序。