---

---

思想

直接对神经元的输出进行批归一化

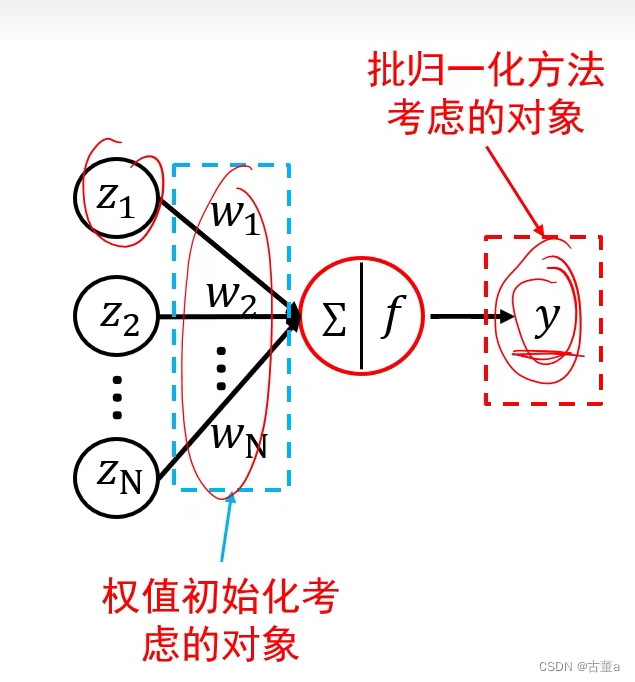
批归一化：对输出值进行归一化，将归一化结果平移缩放作为输出。

批归一化操作

小批量梯度下降算法回顾：每次迭代时会读入一批数据，比如32个样本；经过当前神经元后会有32个输出值y₁,…y₃₂。
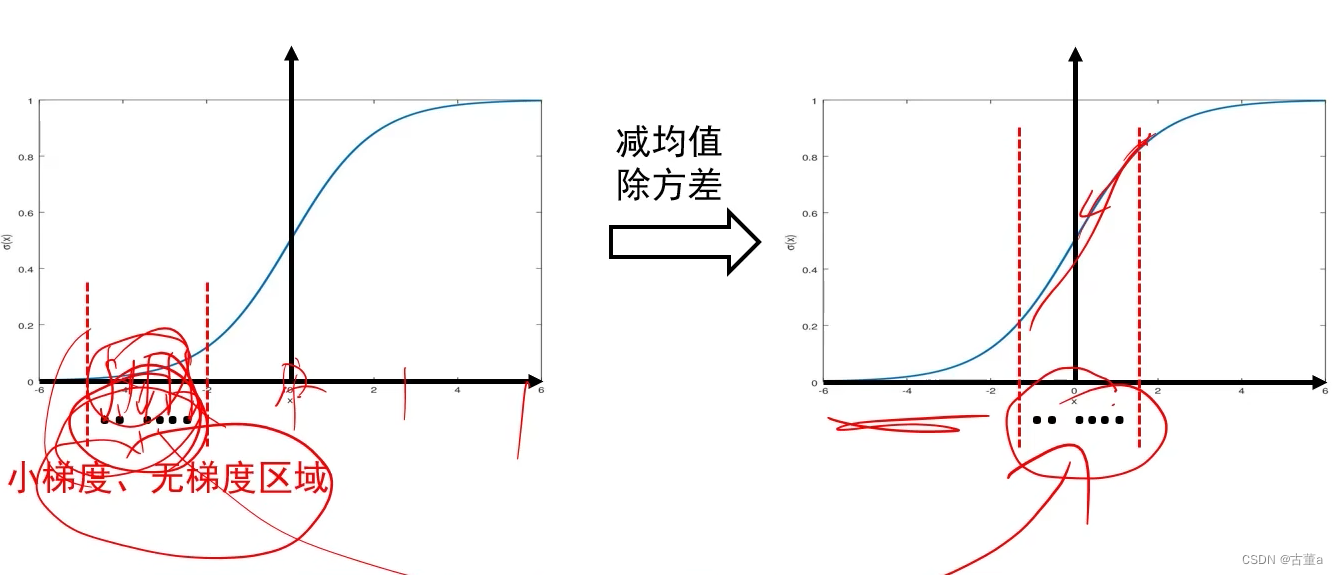
批归一化操作：对这32个输出进行减均值初方差操作；可保证当前神经元的输出值的分布符合0均值1方差。
如果每一层的每个神经元进行批归一化，就能解决前向传递过程中的信号消失问题。

批归一化与梯度消失

实际操作中，经常将批归一化放在全连接层之后，非线性激活前。

FC：全连接层 就是wx+b

经过BN处理

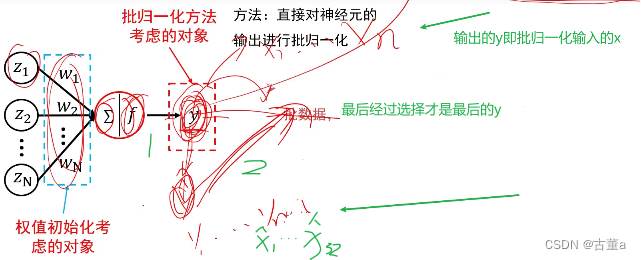
批归一化解决两个问题：

1. 保证前向传播中信息流通畅，不至于让数据变为0导致的数据不能到达输出层。因为每次归一化后数据都会将很小的数据，变得不那么小。
2. 保证反向传播中信息流通畅，可以有效的防止梯度消失现象发生。因为每次归一化后梯度都会变得很有效

算法实现

参数解释：

问题：输出的0均值1方差的正态分布是最有利于网络分类的分布吗 ？

根据对分类的贡献自行决定数据分布的均值与方差

平移缩放的作用

可以使网络自行选择数据分布的均值和方差，γ决定方差，β决定期望。γ和β是学习参数，不是超参数，需要神经网络学习得出。

问题：单张样本测试时，均值和方差怎么设置？

来自训练中。累加训练中每个批次的均值和方差，最后进行平均，用平均后的结果作为预测时的均值和方差。