李宏毅机器学习第一课

机器学习就是让机器找一个函数f，这个函数f是通过计算机找出来的

如果参数少的话，我们可以使用暴搜，但是如果参数特别多的话，我们就要使用Gradient Descent

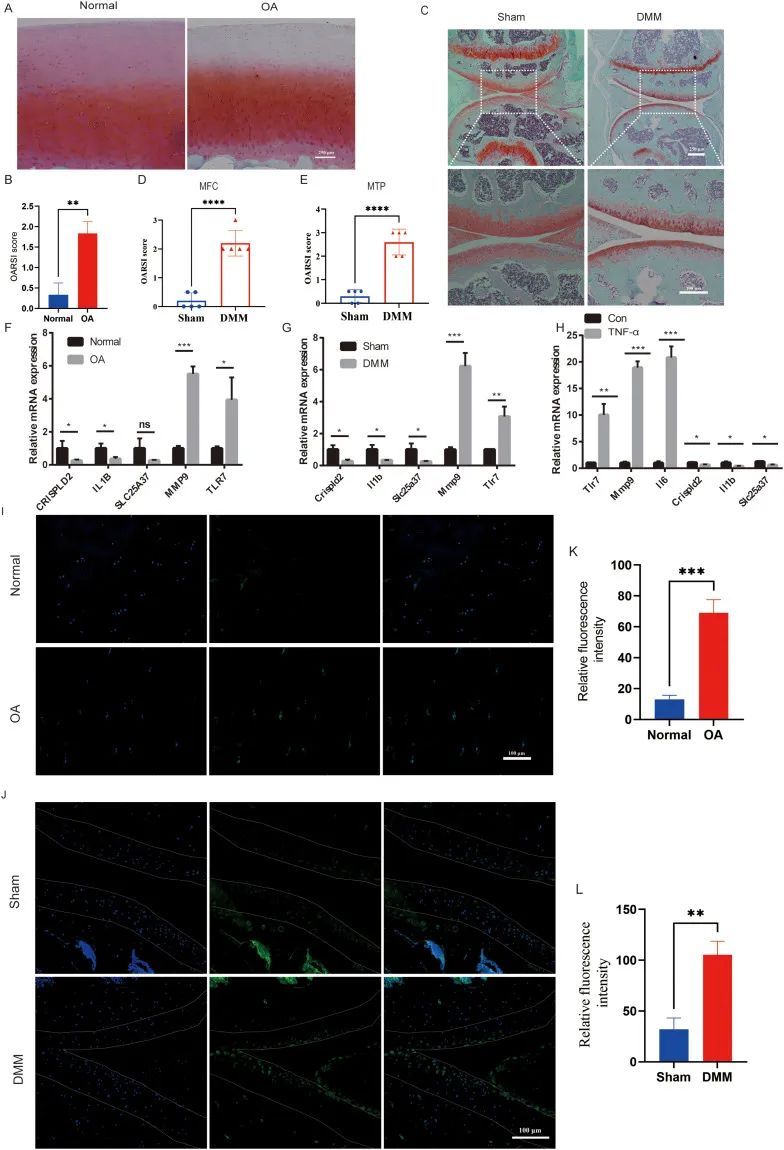
Regression (输出的是一个scalar数值)

Classification （在设定好的选项，两个或者多个，中做出选择）

Structured Learning （画一张图，写一段文字，让机器学会创造）

机器人寻找一个函数式子有三个步骤

一：function with unknow parameters

我们需要基于domain knowledge 来猜测确定一个函式，这个函数就是model

feature x 是我们已经知道的数据， weight w、 bias b 是未知的参数， label 是一个正确的数值

hyper parameters是我们在机器学习的时候，我们自己设置的参数

y = b + wx

二：Difine Loss

本质上也是一个function ，输入是上面b和w，输出的值代表输入的b和w好还是不好

label是真实的数据

我们根据y = b + wx来预测数据，和label之间的差距取一个绝对值

然后吧每一组数据都计算y^ ，然后加总求一下平均值

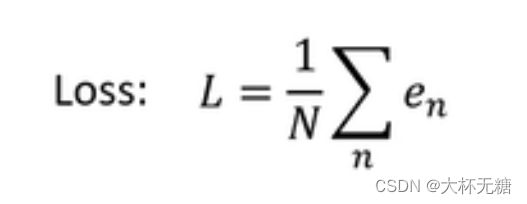
e = |y - y^| 如果用这种方式来计算的话， L is mean absolute err (MAE)

具体用哪一种函数来衡量这一组参数的好坏，取决于对问题的本质的理解

Error Surface 是等高线图，是尝试了多个w和b之后的结果

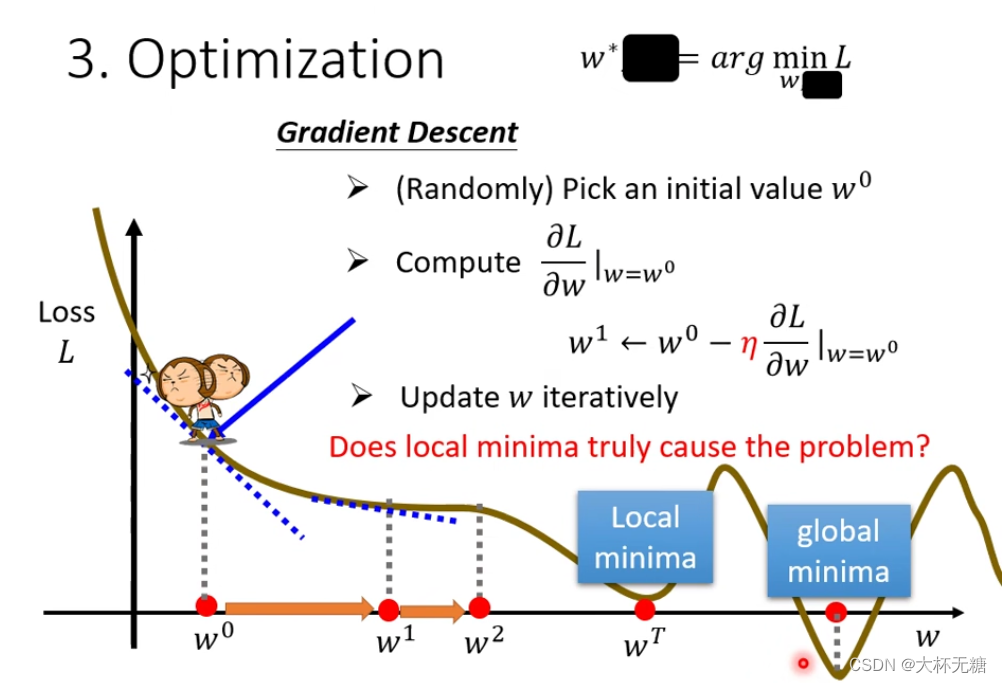
三：Optimization

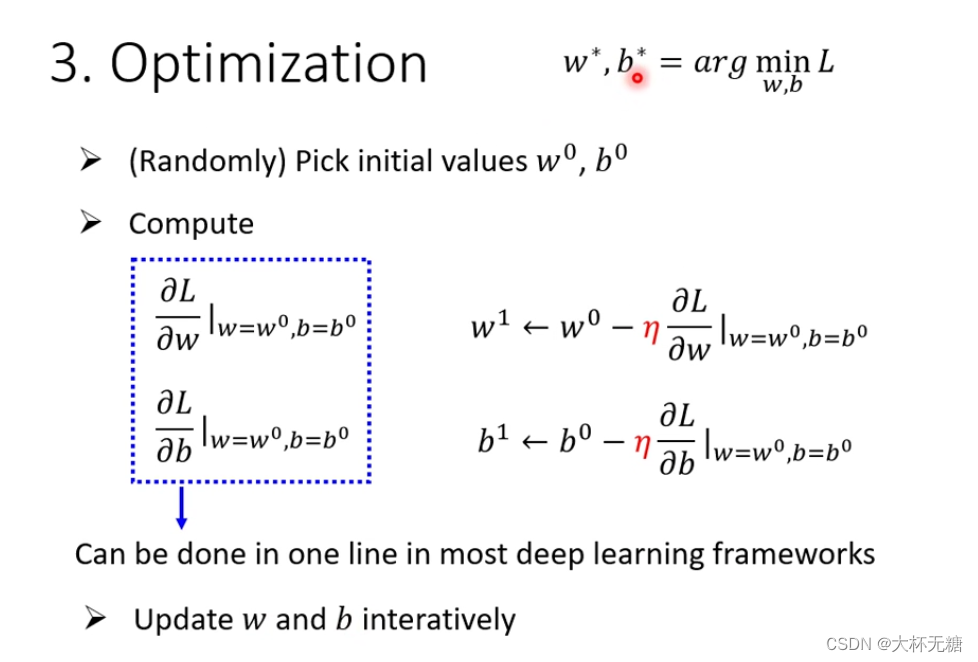
是找一个最好的w和b，叫做w*和b* ，用到的方法是Gradient Descent，

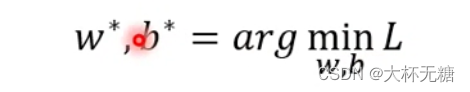
假设现在只有一个参数

假设现在有两个参数，和之前一个参数其实一样的

上面三个步骤，是在做机器学习的训练

我们之后还需要做预测

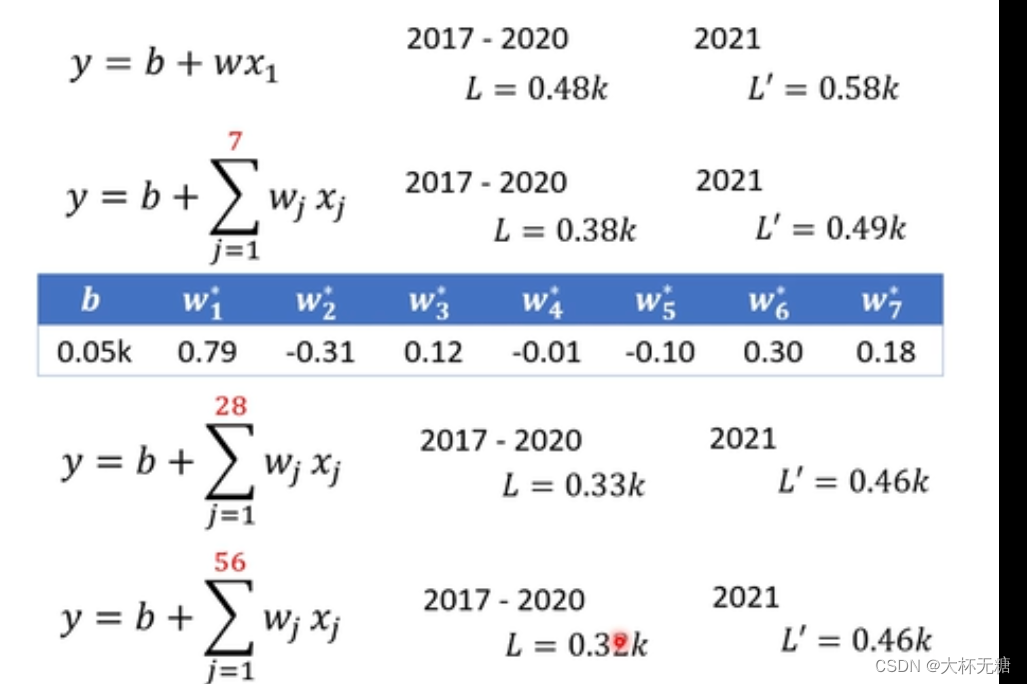
训练的数据和预测的数据做一个对比，发现后者的loss比前者的loss大，这说明，我们在预测已经存在的数据的效果比较好，但是预测未知的数据效果比较差

我们需要修改模型，对模型的修改，往往来自于对问题本质的理解，我们修改了模型，让分别考虑前七天，前28天，前56天等等

model bias

上面的所有模型都是Linear model ，也许Linear模型过于简单，我们可以修改w，修改b，但是模型始终都是一条直线，我们始终无法实现红色的这种模型

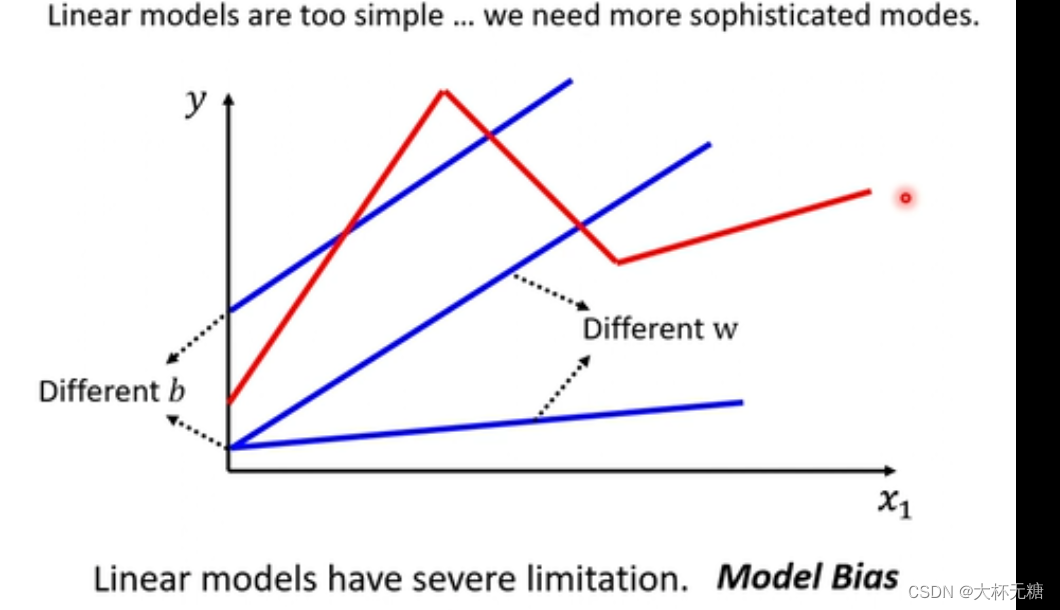
Linear models本质是一条线性直线，但是很多问题不是Linear models，Linear models 有很大的限制，来自于model的限制叫做model bias

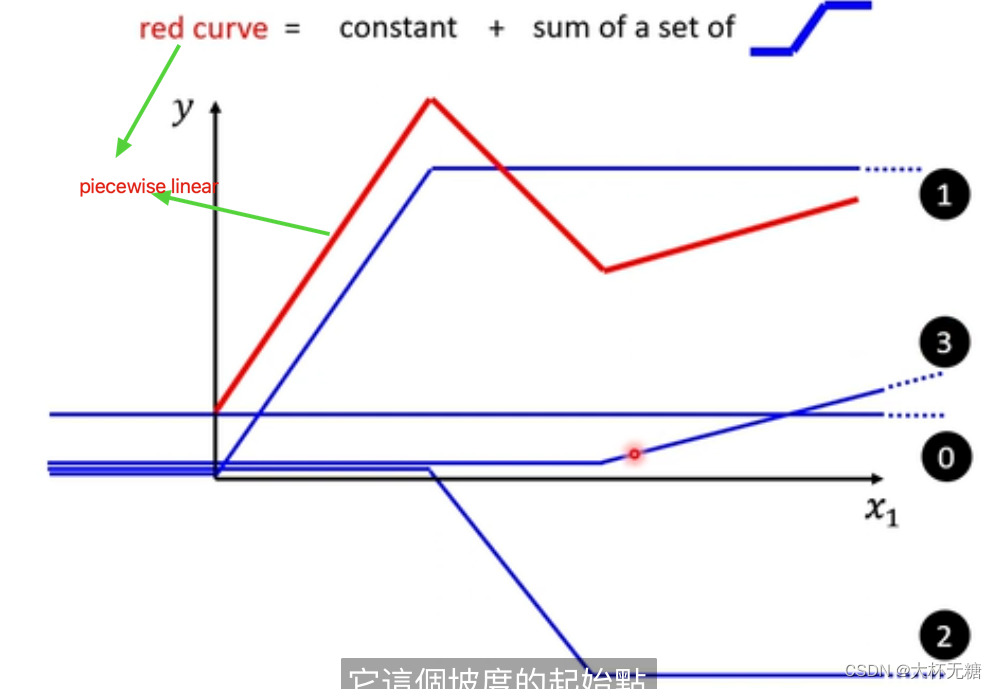
piecewise Linear Curves

我们可能是想要piecewise Linear Curves （分段线性曲线：一种由多个线性部分组成的曲线，每个部分都是线性的，但整体上可能不是线性的），我们其实可以通过下面的方式达到这种效果，我们可以是所有一系列下面蓝色的function

再也许piecewise Linear 也无法满足我们模型的需求了，我们想要的是曲线，如下图所示

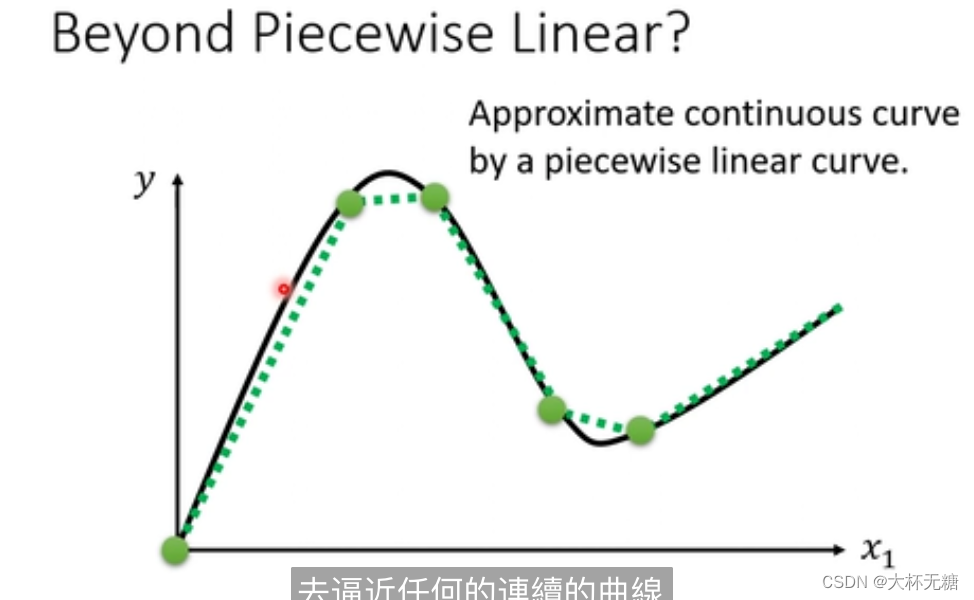
piecewise Linear Curves 足够多，可以逼近曲线，此时所有的 piecewise Linear 虽然是直线，但是已经达到了曲线的效果

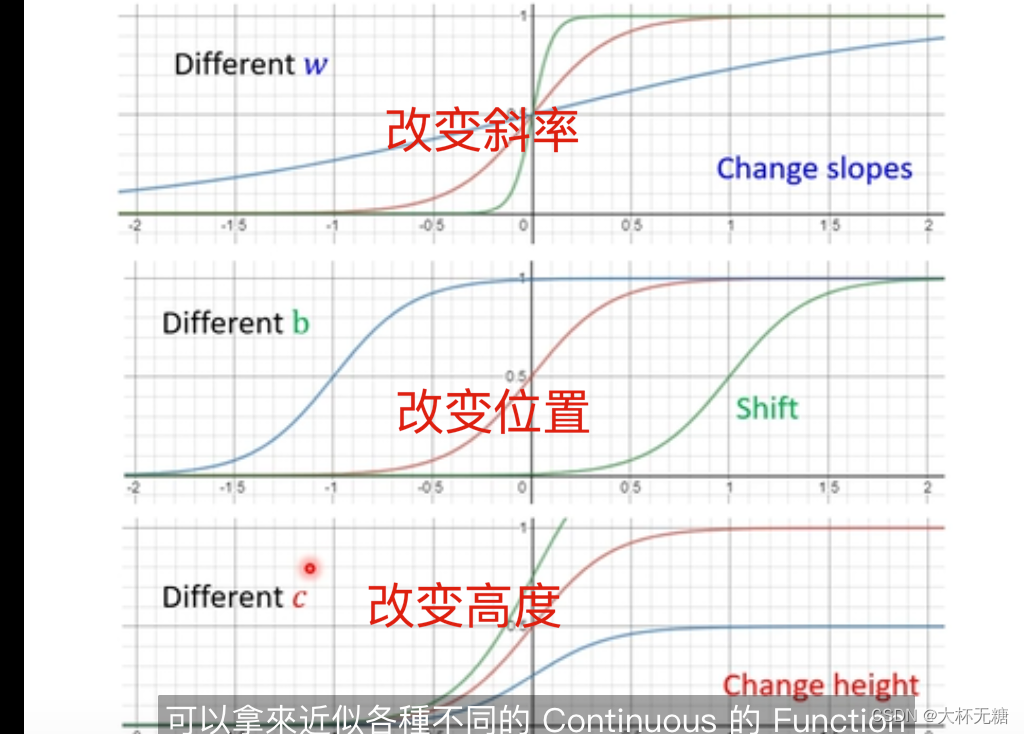
那这个蓝色的function （Hard Sigmod）是什么呢？如何把蓝色的function写出来呢？

其实就是用sigmoid函数来逼近蓝色的function

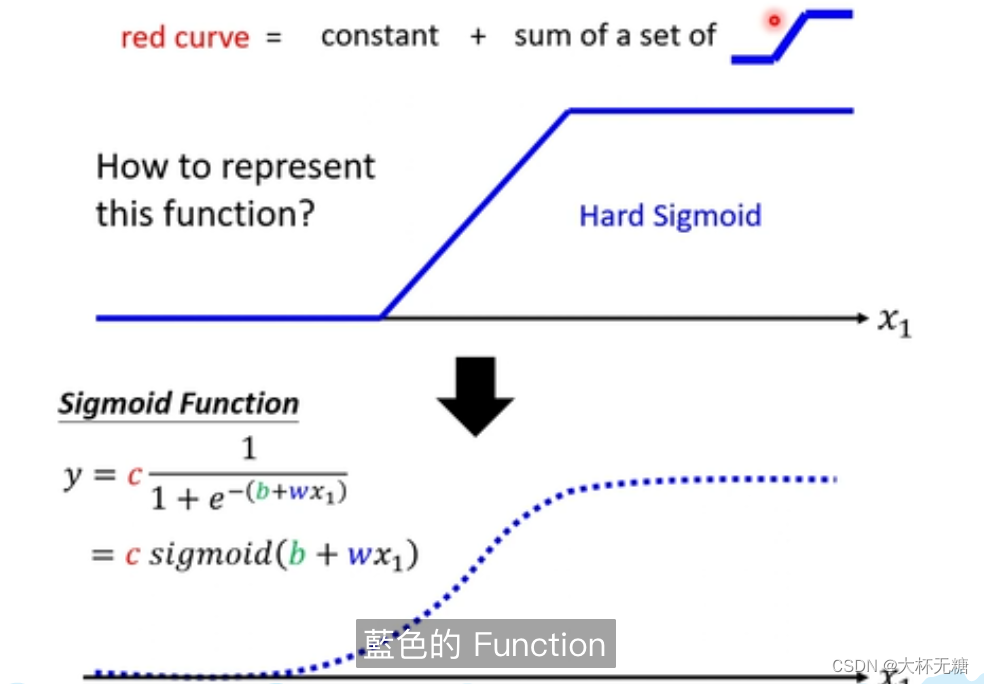
我们需要各种各样的蓝色的function，那我们可以通过调整b和w来实现

所以，我们需要一个红色的function，就可以通过下面的方式来实现，同时我们既然实现了红色的function，我们可以实现和红色类似的曲线（Continuous）

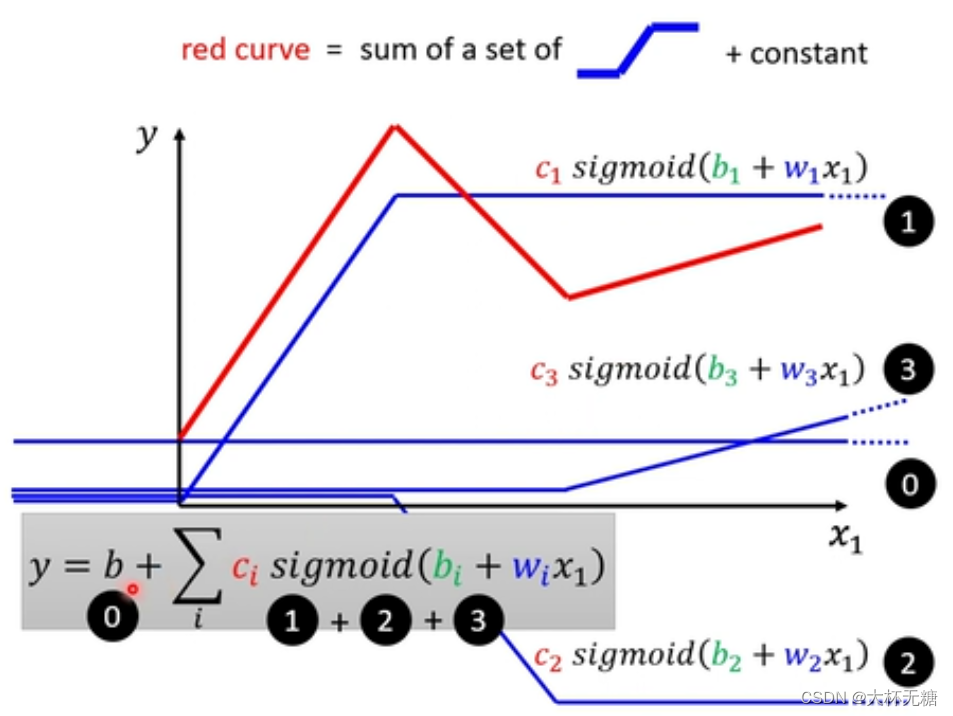
所以，我们解决了model bias的问题

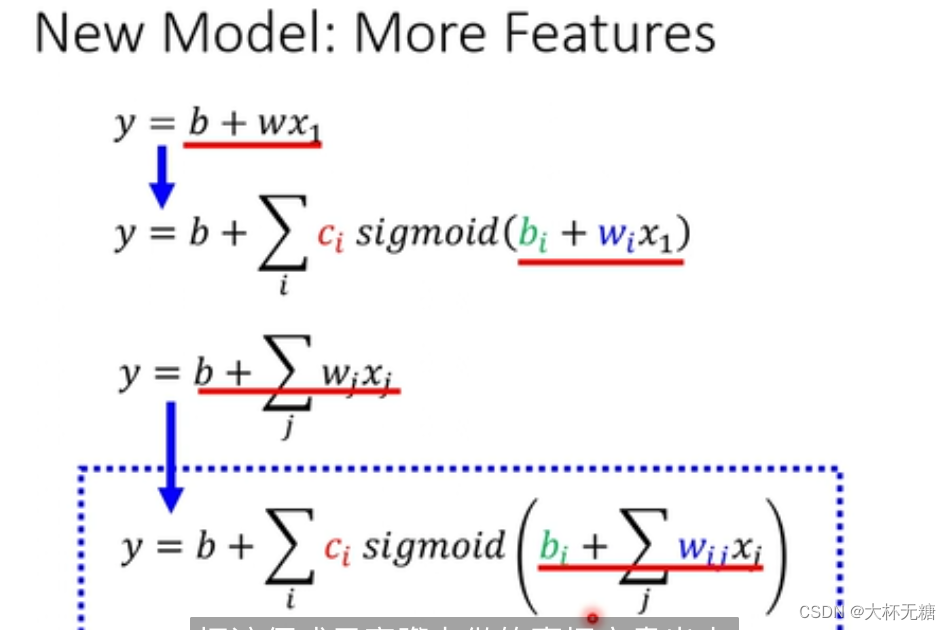
如何计算这个式子呢？

用线性代数的表示方式表示如下：

输出=w1⋅x1+w2⋅x2+…+w8⋅x8+偏置项

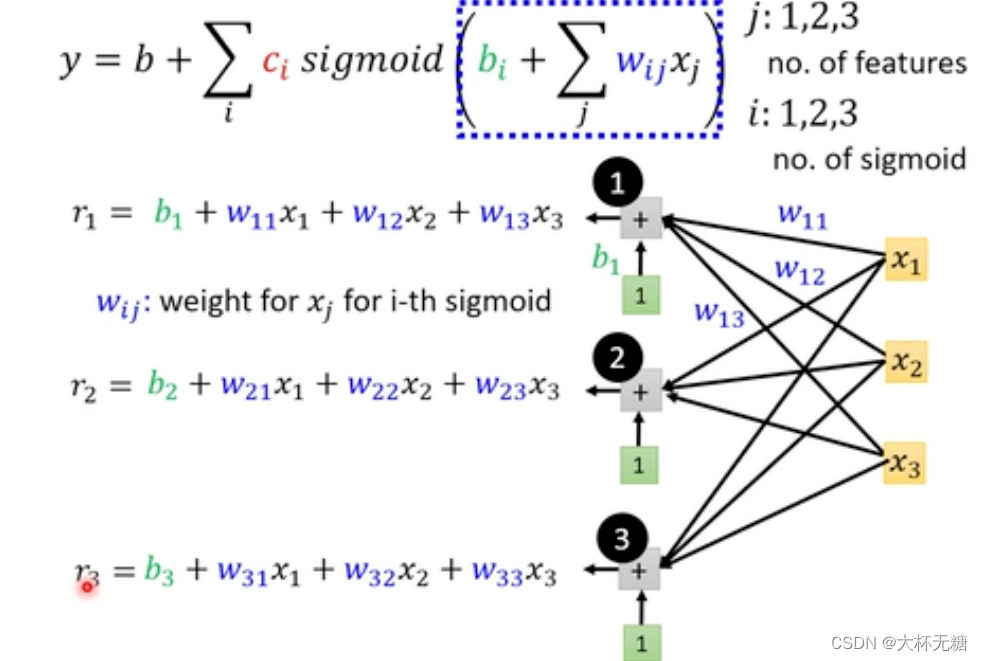
最后总的表示一下

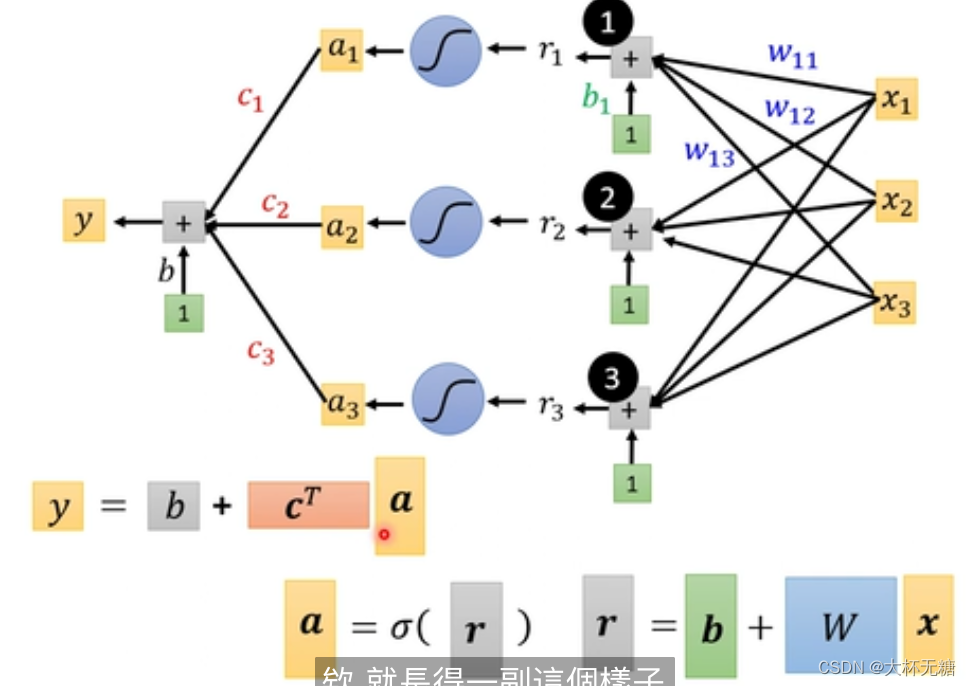
这里面，除了x是feature，其他都是未知的参数，我们使用线性代数的方式来统一表示

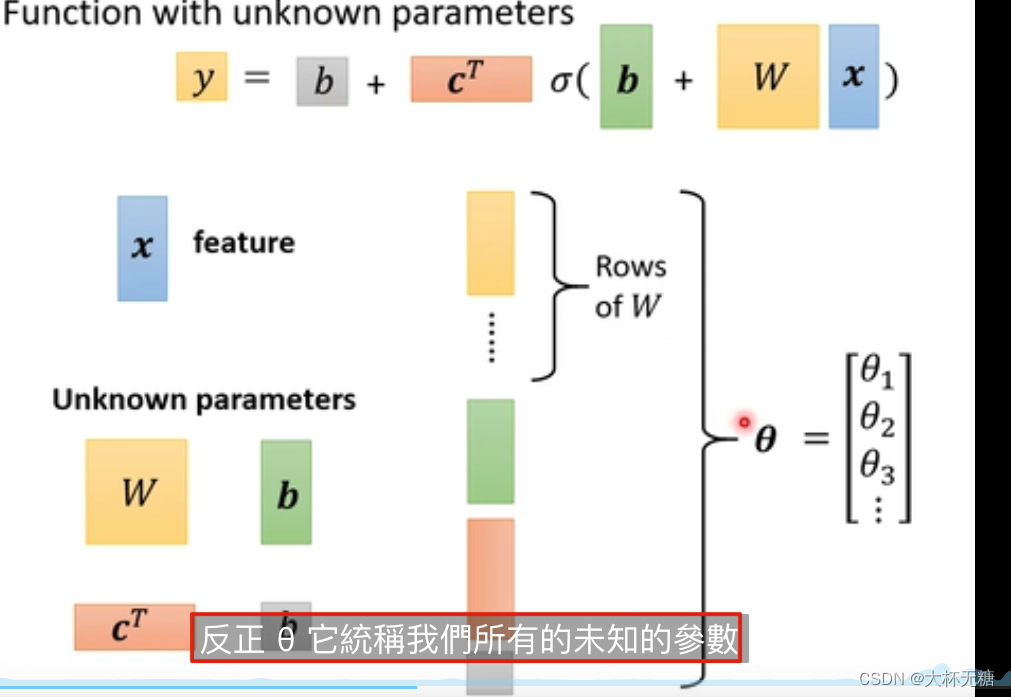
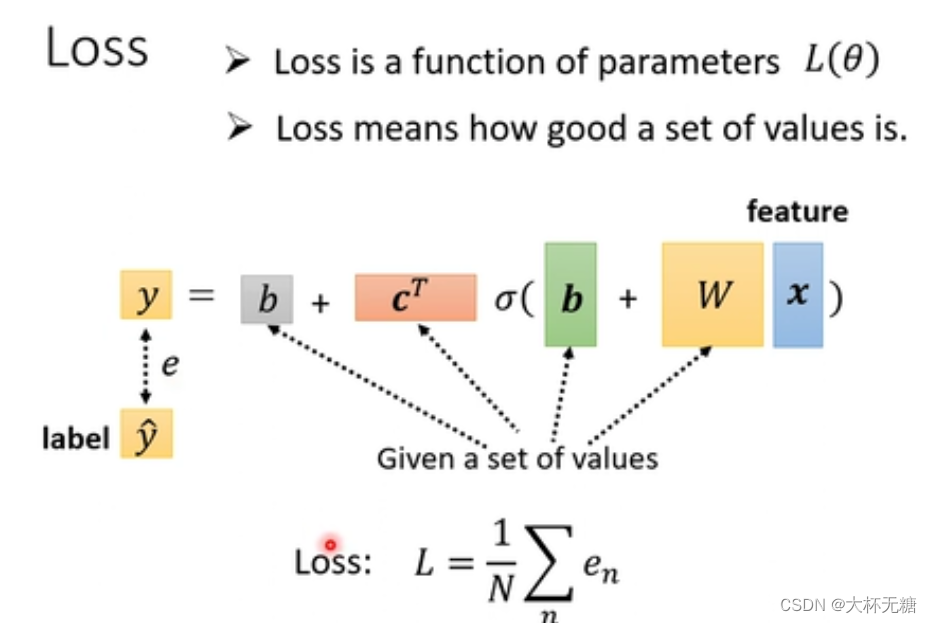
模型定义解决了，接下来是第二步定义Loss function，跟之前是一模一样的

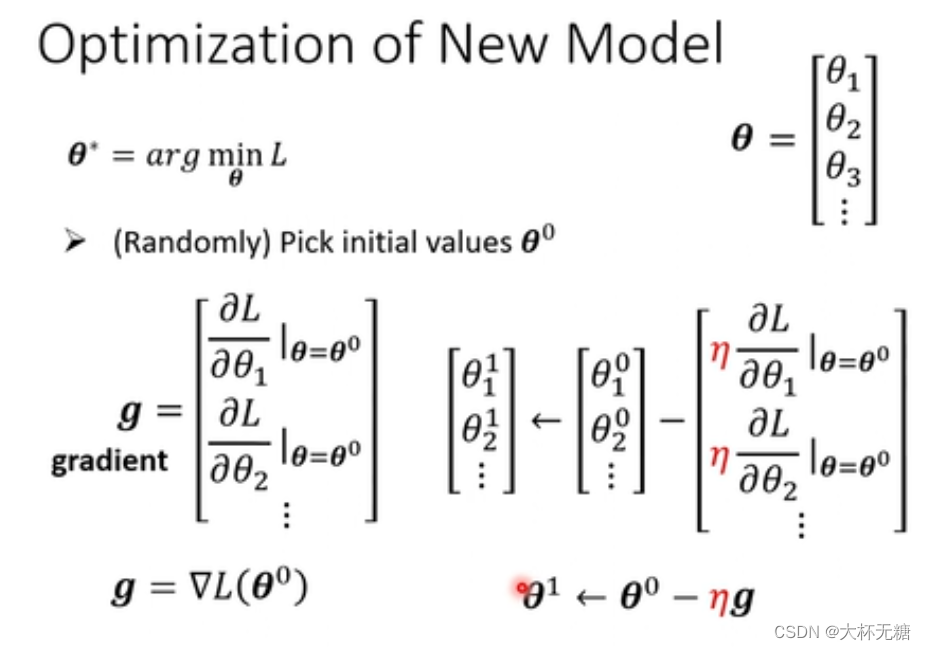
第三部optimization ，也是一模一样

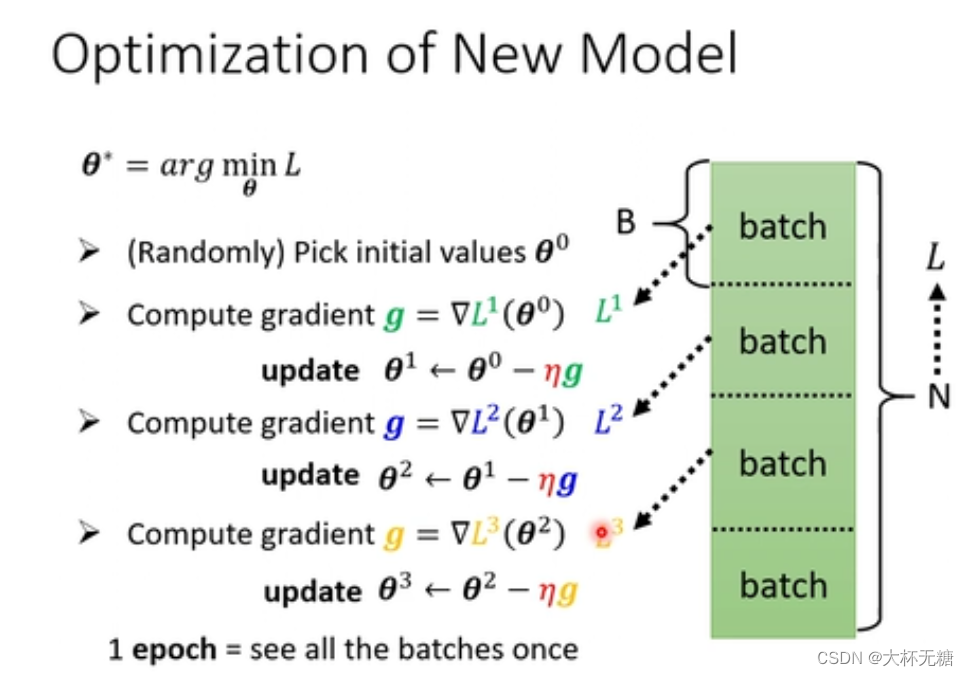
Batch 、 Epoch

我们在之前计算loss的时候，是把所有的data都参与进去，但是现在的话，我们是把data分成 L 笔，每一笔就是一个batch ，每个batch都计算loss，每次根据计算出来的loss然后对当前参数进行微分，一直把所有的batch完成，这就是一个epoch，一个epoch中会update N / B = L次参数

我们刚才是使用sigmoid函数来模拟蓝色的function （ hard sigmoid ），多个hard sigmoid 叠加，从而实现红色的function

但是这个蓝色的function ，也可以不用sigmoid函数模拟，我们可以使用两个Rectified Linear来实现蓝色的function

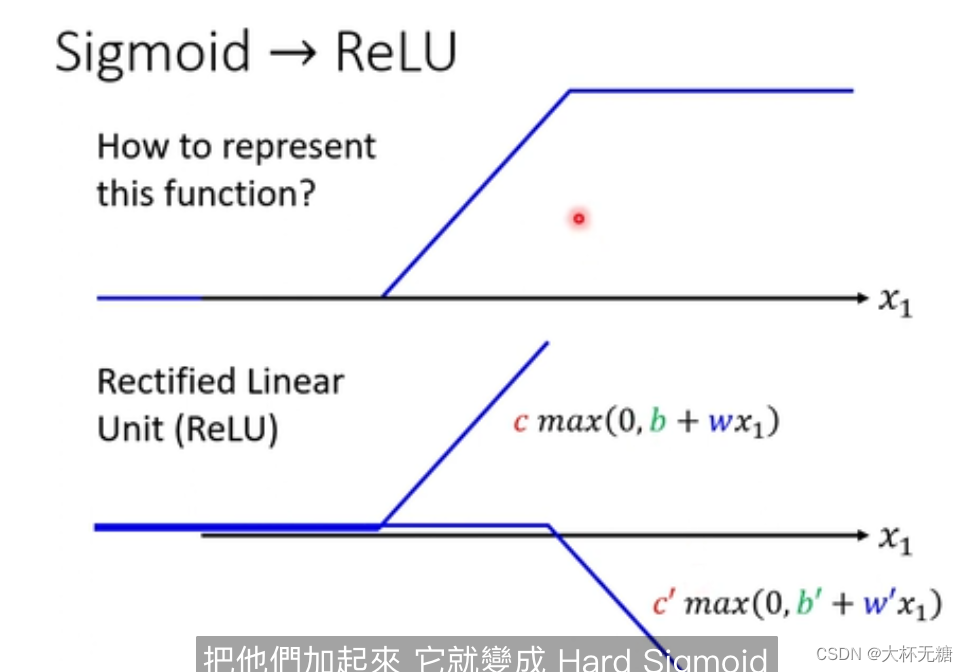
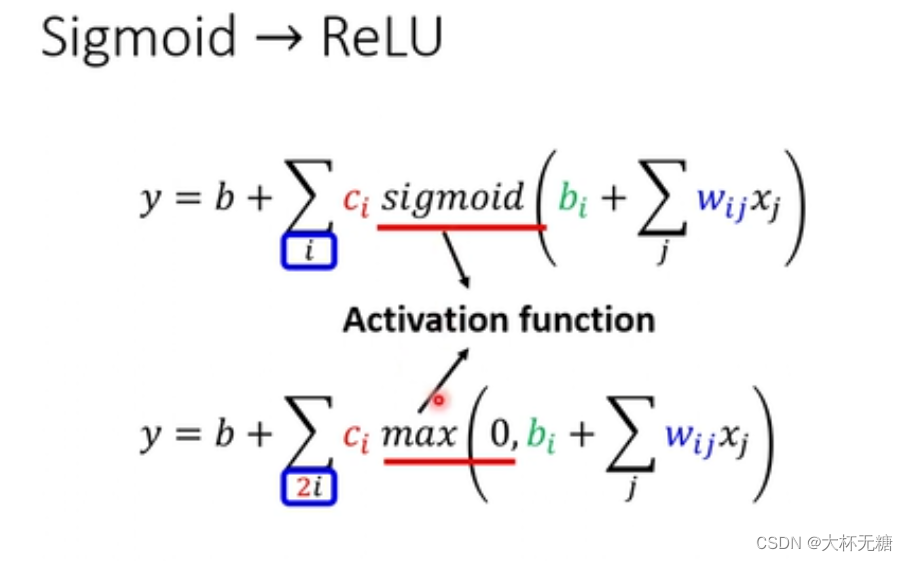
Activation Function ： Relu和sigmoid

ReLU和sigmoid那个好呢？后续会讲解

我们使用1000个Relu函数之后，就可以实现很复杂的函数，效果会有改善

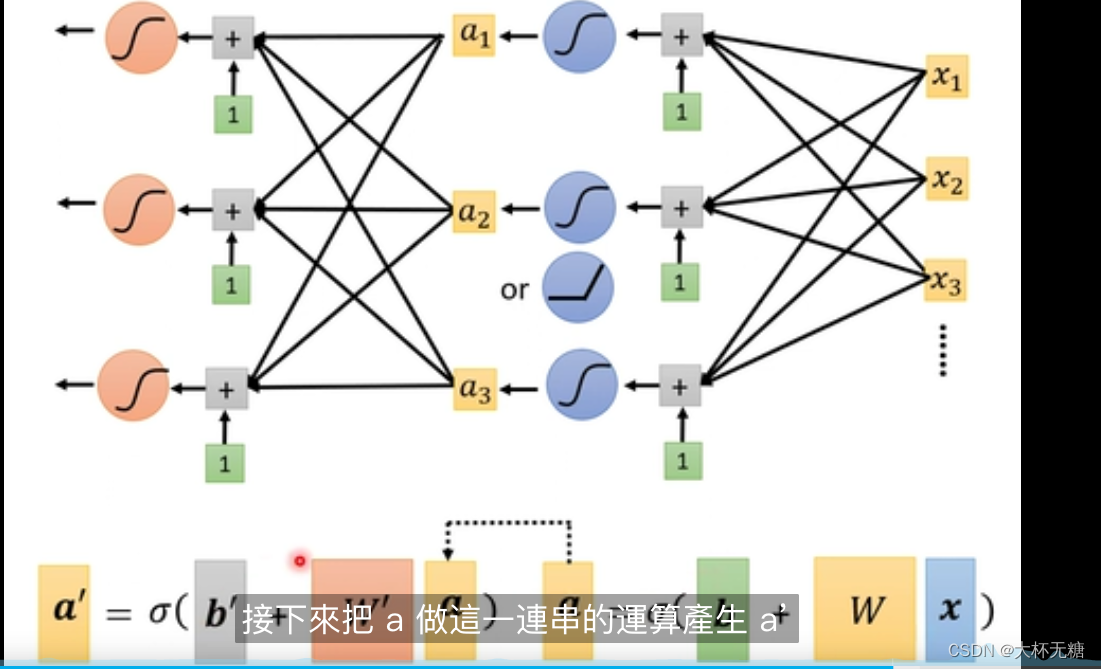
Deep Learning

深度学习，我们计算出来的a，我们再把a重新放入函数中，再计算很多次

Overfitting

Better on training data， worse on unseen data

作业一的模型

self.layers = nn.Sequential(# 这个地方函数都是有参数的， 只是没有写出来# y[0] = weight[0][0] * x[0] + weight[0][1] * x[1] + ... + weight[0][input_dim - 1] * x[input_dim - 1] + bias[0]# y[1] = weight[1][0] * x[0] + weight[1][1] * x[1] + ... + weight[1][input_dim - 1] * x[input_dim - 1] + bias[1]# ...# y[15] = weight[15][0] * x[0] + weight[15][1] * x[1] + ... + weight[15][input_dim - 1] * x[input_dim - 1] + bias[15]# 类似于视频中YouTube观看人数预测，如果考虑七天，input_dim就是7，如果考虑28天，input_dim就是28nn.Linear(input_dim, 16),  # 这个是一个线性层# 对于每个输出维度y[i]（其中 i是从0到15的索引），ReLU激活函数将执行以下操作：# y[i] = max(0, y[i])nn.ReLU(),  # 激活函数，我们可以对上面的结果进行Relu操作nn.Linear(16, 8),nn.ReLU(),# 具体地，线性映射通过一个权重矩阵和一个偏置项来实现，将每个输入维度与相应的权重相乘，然后将结果相加，再加上偏置项。nn.Linear(8, 1)  # 因为我们最终是要预测一个数字结果，所以这个地方要是一维的# 视频上面预测Youtube人数，就是nn.Linear(3,1)，视频上面直接就是输出的一维结果)

nn.Linear(input_dim, 16)，为什么要输出16维度的结果？

input_dim就对应视频中的考虑7天，28天，56天等等

16 代表输出的是一个16维度的结果，这个就是我们自己设置了

Linear 里面有很多的weight参数和一个bias参数，这些我们看不到，但是pytroch帮我们做好了，机器学习就是在找这些参数。

chatgpt回复：是的，你可以将模型中的16更改为32，以增加隐藏层的维度。这将增加模型的复杂性，并有可能提高其性能，尤其是在处理更复杂的数据或任务时。但请注意，增加隐藏层维度也会增加模型的计算复杂度，因此你可能需要更多的数据来训练模型，以避免过拟合。

你可以像这样更改模型的隐藏层维度：
self.layers = nn.Sequential( nn.Linear(input_dim, 32), # 将16更改为32 nn.ReLU(), nn.Linear(32, 8), # 这里也需要相应地更改输入和输出维度 nn.ReLU(),nn.Linear(8, 1))
记得根据你的数据和任务来调整模型的参数，以获得最佳性能。如果你的数据集较小，你还可以考虑使用正则化技巧来防止过拟合。

隐藏层的维度通常是根据你的具体问题和数据来确定的，而不是一个固定的数值。选择隐藏层维度通常是深度学习模型设计中的一个超参数，需要进行调优。