一、选择排序
1.1 选择排序思想
先把最小的元素拿出来
剩下的,再把最小的拿出来
剩下的,再把最小的拿出来
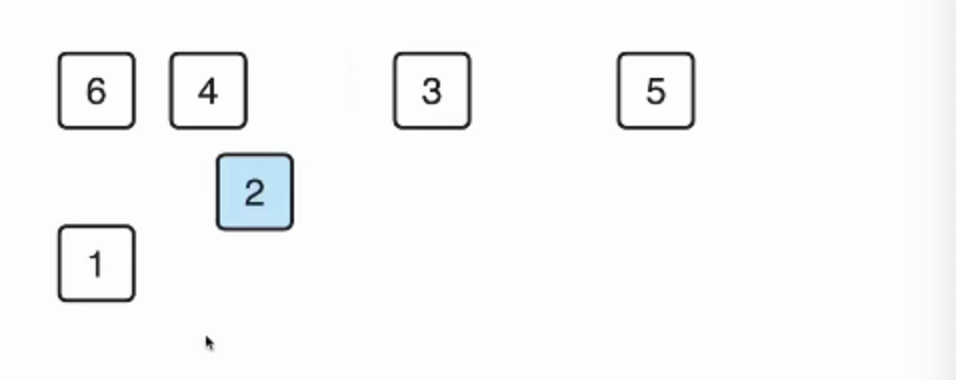
但是这样 空间复杂度是O(n)
优化一下,希望原地排序
1.1.2 选择原地排序

索引i指向0的位置
索引j指向i+1的元素
j 后面的元素遍历,找到最小的标记为minindex
交换minindex 和 i

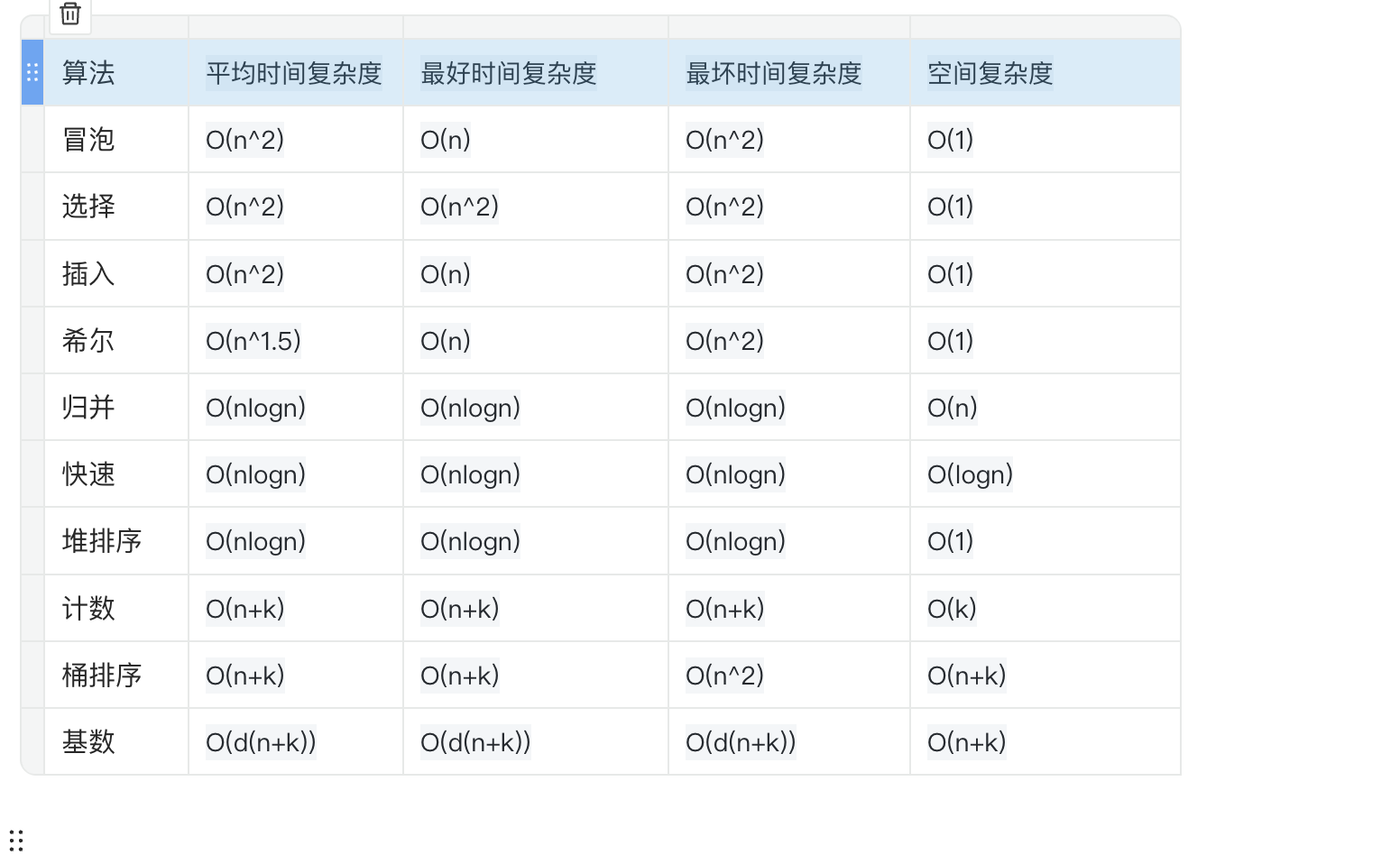
时间复杂度O(n^2)
空间复杂度O(1)
1.2 选择排序复杂度

第一轮 n 次,第二轮 n-1 次
1 + 2 + 3 + … + (n-1) + n
二、插入排序

扑克牌的排序 就是 插入排序
2.1 插入排序思想

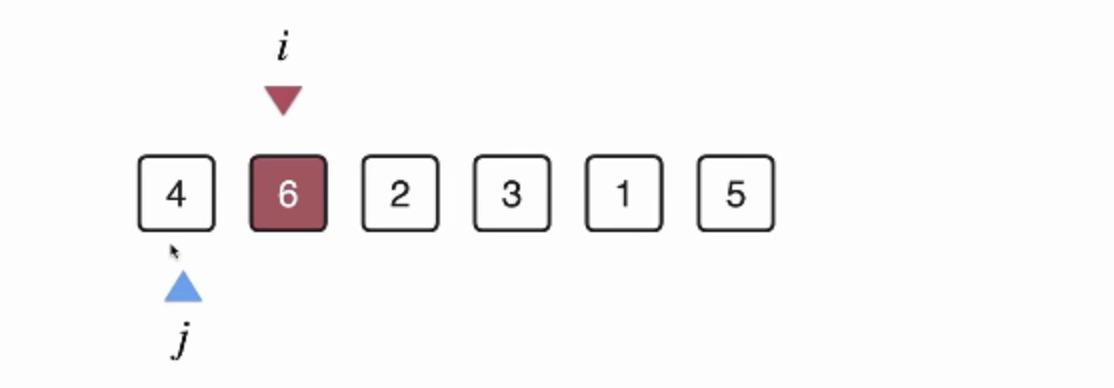
j 往前 插入
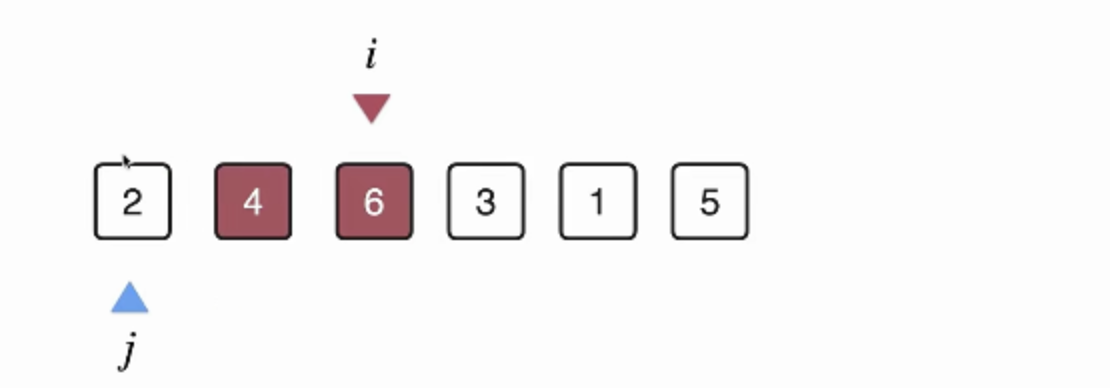
时间复杂度O(n^2)
空间复杂度O(1)
三、冒泡排序
基本思想:每次比较相邻的元素
3.1 冒泡基本思想
- 第一轮两两比较大小
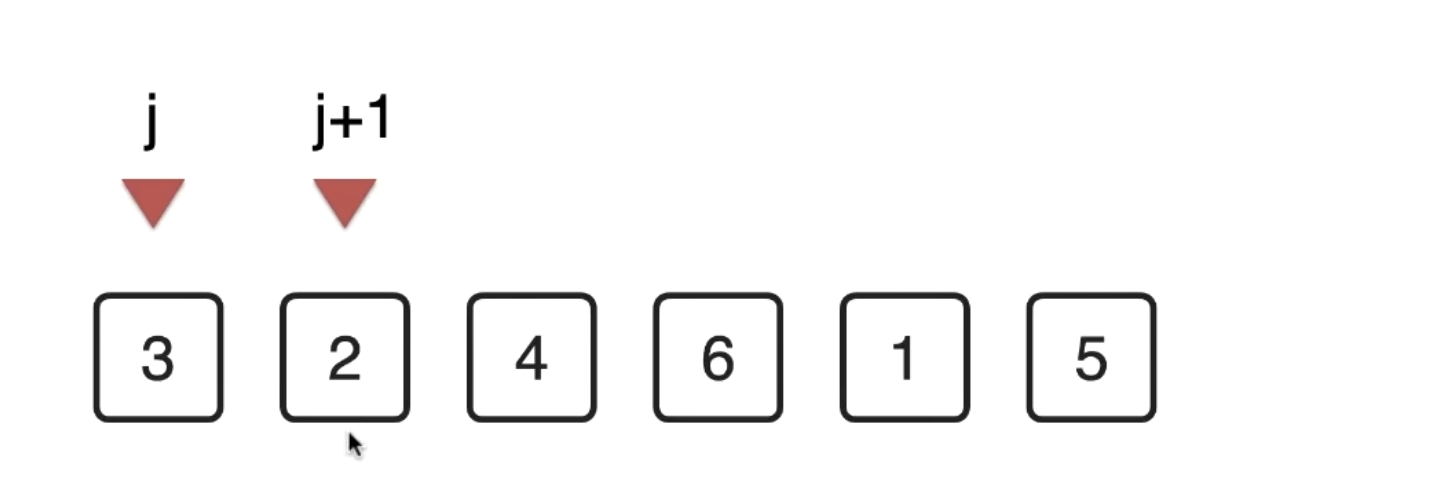
如果 > ,就互换
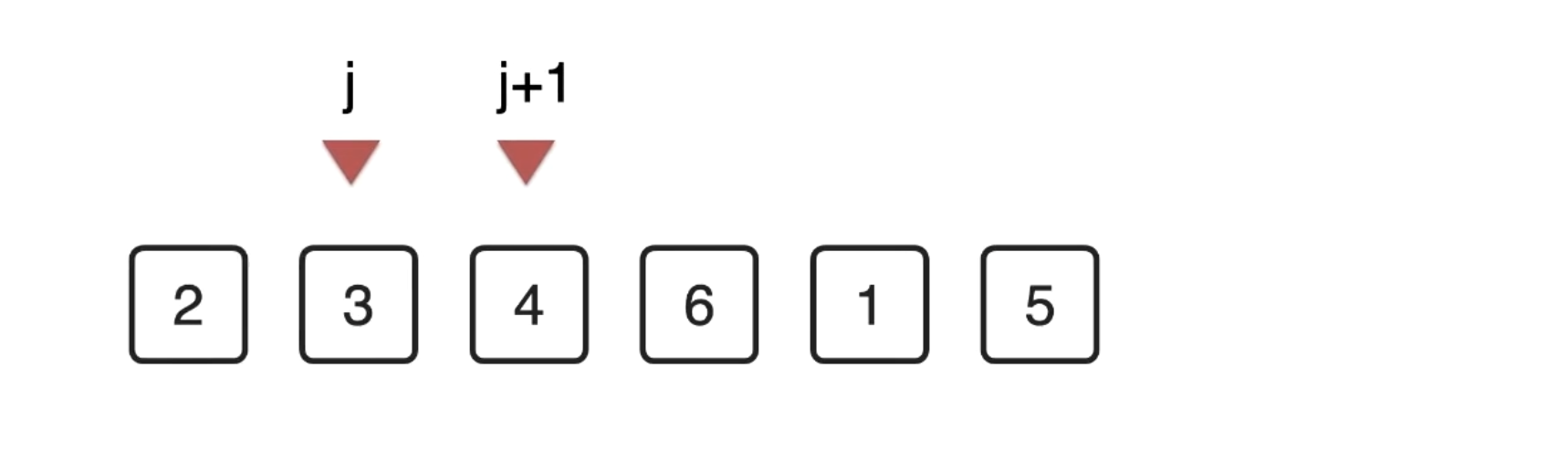
一直到最后
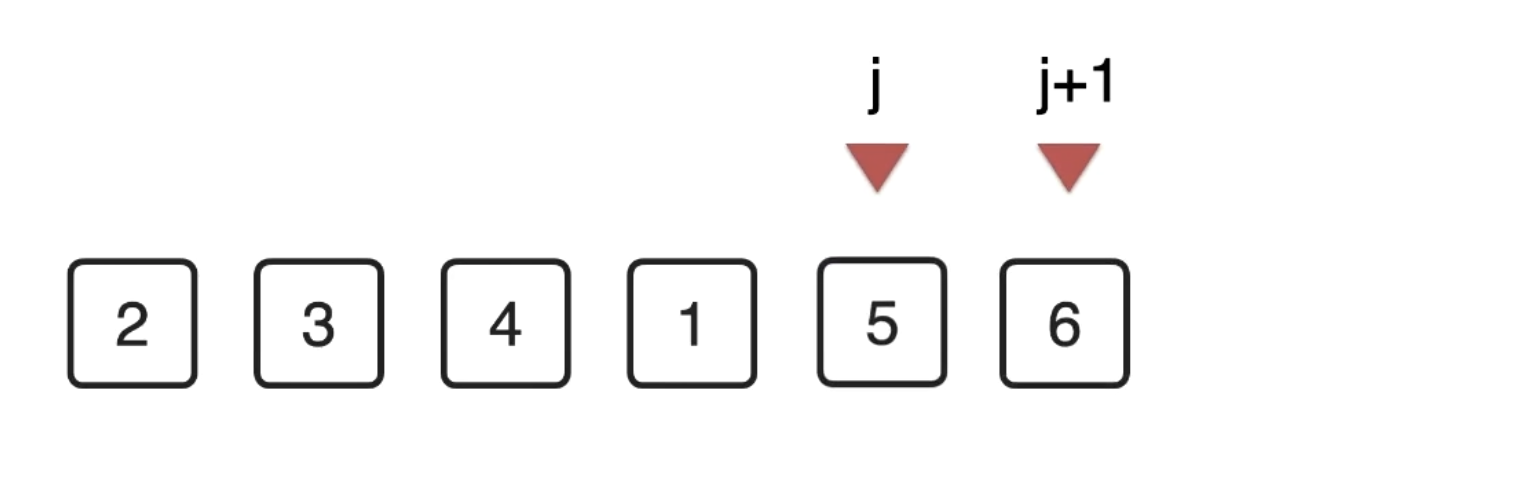
第一轮之后,最大的元素一定在最后
所以在第二轮,最后一个元素就不用比较了
- 第二轮
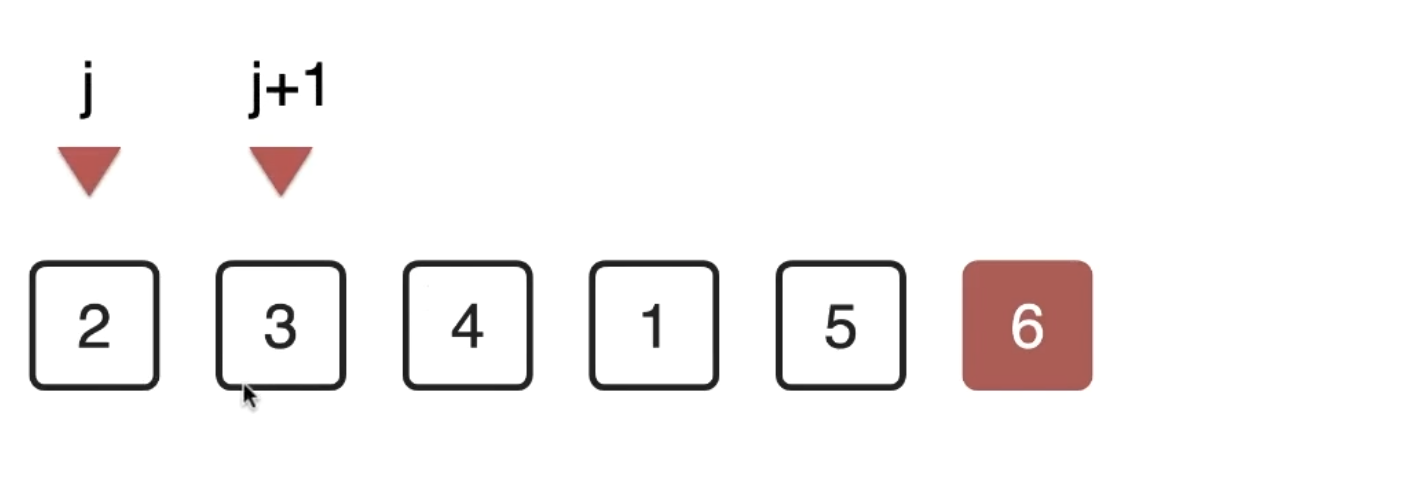
- 第三轮
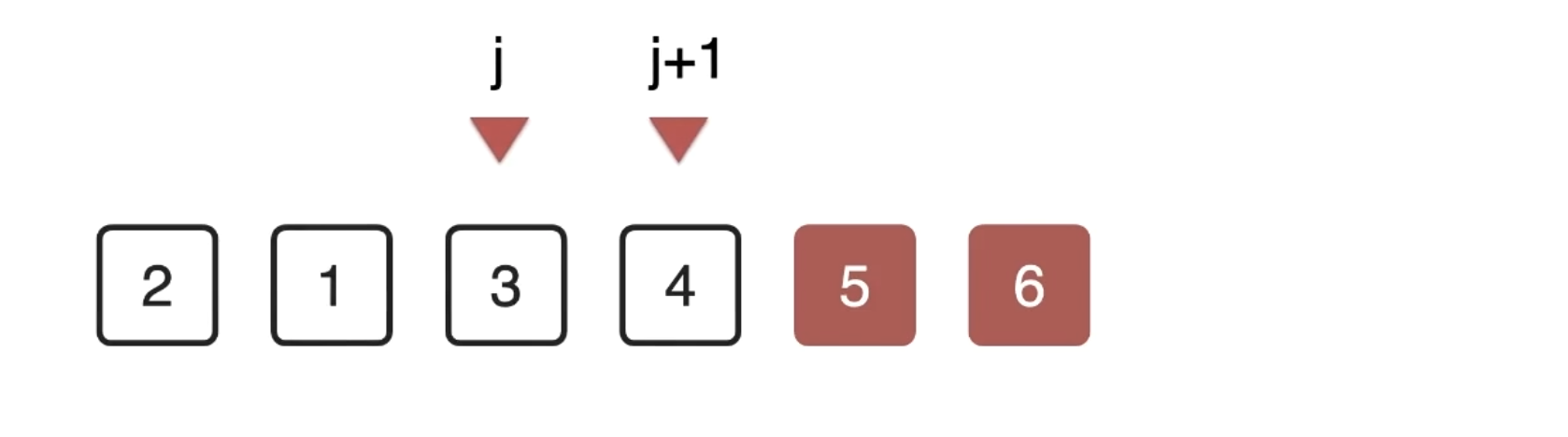
- 第n - 1轮

3.2 冒泡过程理解

平均时间复杂度:O(n^2)
空间复杂度O(1)
一、归并排序MergeSort
更加复杂的递归算法
O(nlogn)的时间复杂度
1.1 归并思想
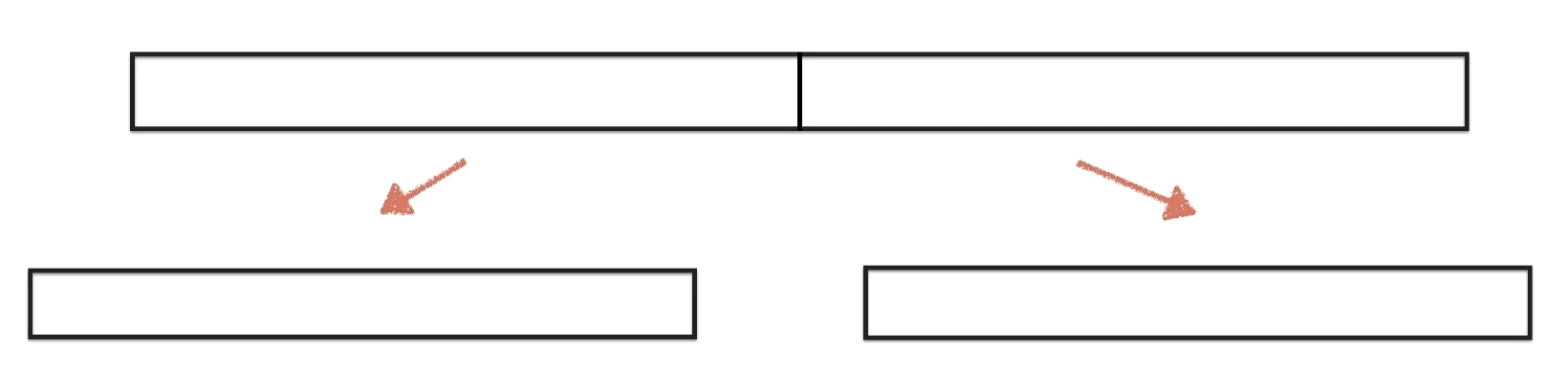
将一个数组一分为二 ,分别排序,得到两个排序后的子数组
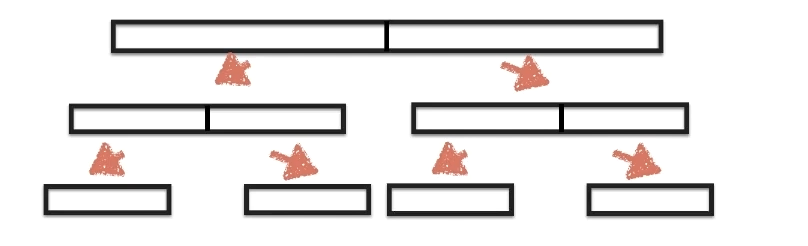
对两个子数组排序的方法还是继续划分
MergeSort(arr, l, r)
对 arr数组的 l 到 r 区间进行排序
1.2 归并步骤
- 递归排序的算法:
MergeSort(arr, l, r)
- 找到切分的中点
int mid = (l + r) / 2
- 对arr[l , mid] 进行排序
MergeSort(arr, l, mid)
- 对arr[mid + 1, r] 进行排序
MergeSort(arr, mid+1, r)
- 将arr[l,mid] 和 arr[mid+1,r]进行合并
merge(arr, l, mid, r)
- 设置递归调用的终止条件
if(l >= r) return;

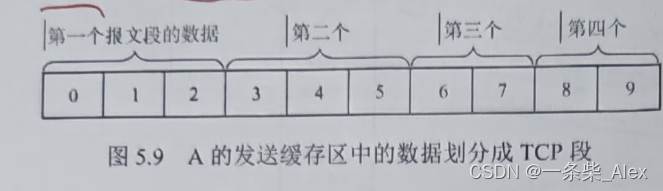
1.3 归并merge过程思想
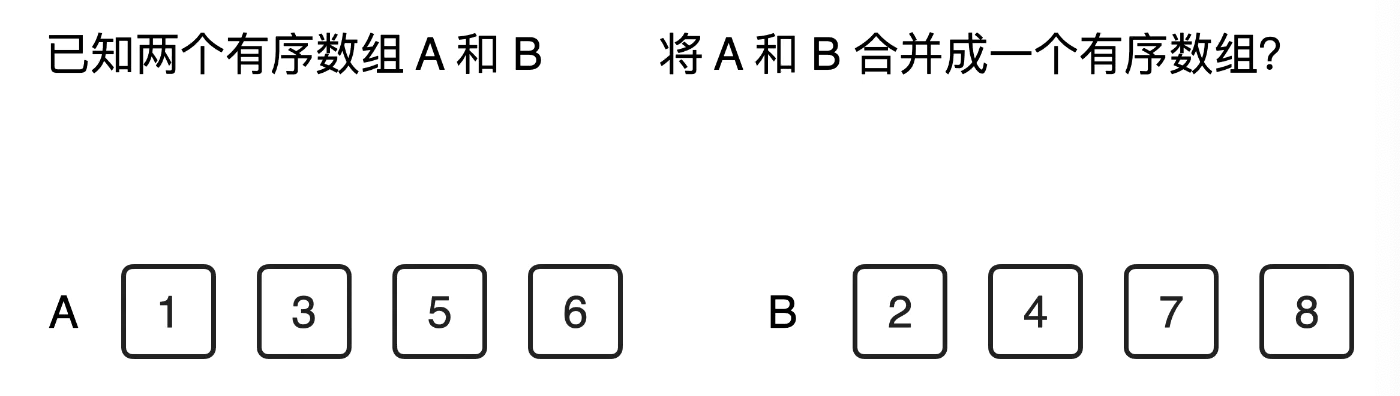
- A[1] 和 B[1] 对比,谁更小,谁进入Result
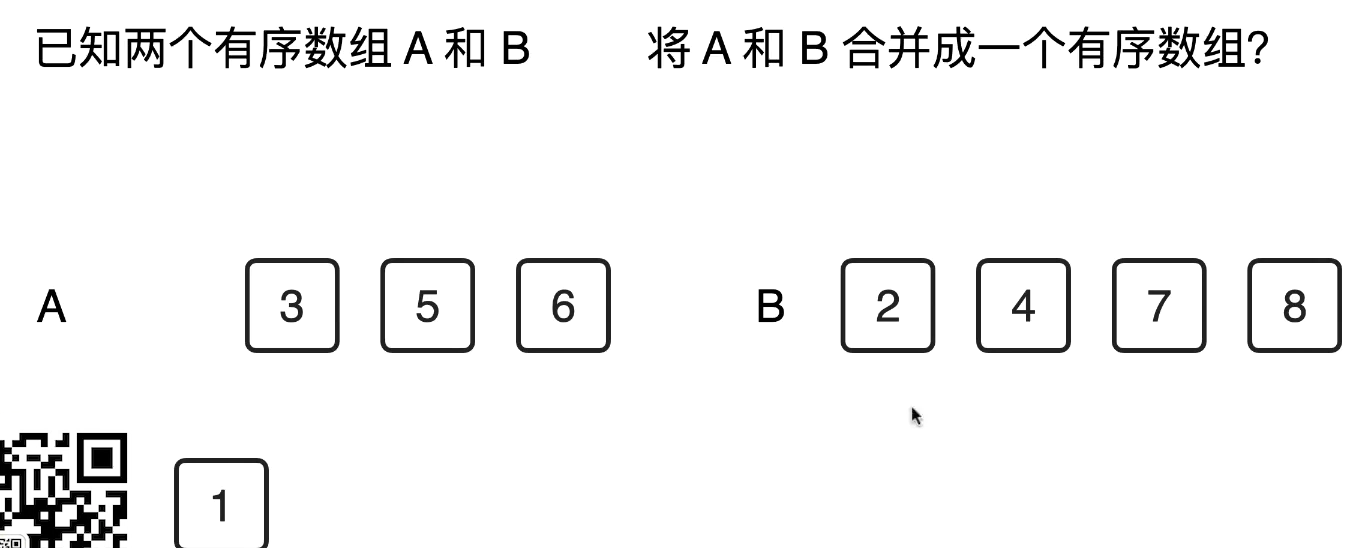
- 持续对比头上的点
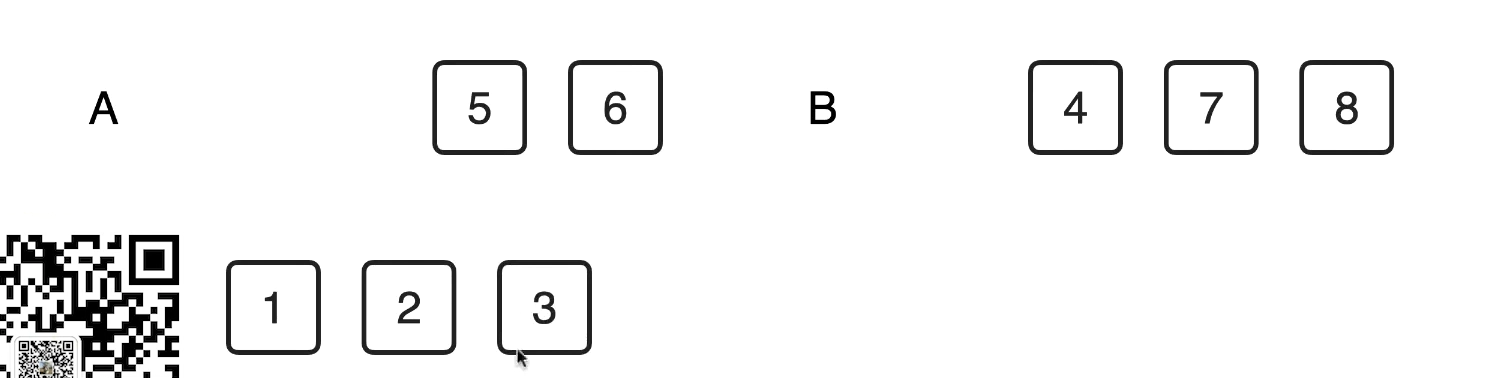
1.4 merge 过程详解
-
计算mid
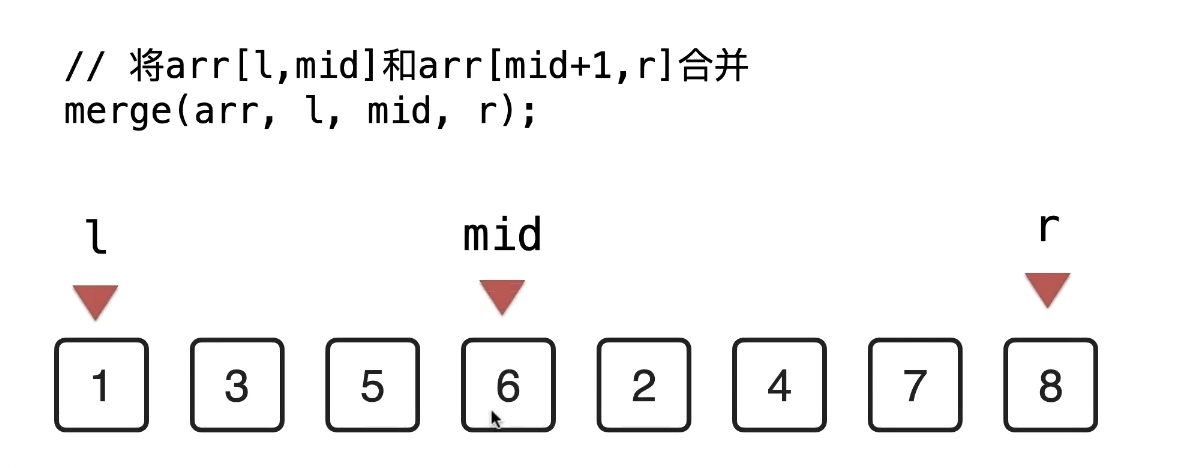
-
将数据复制一份,标记左右 i , j = mid + 1
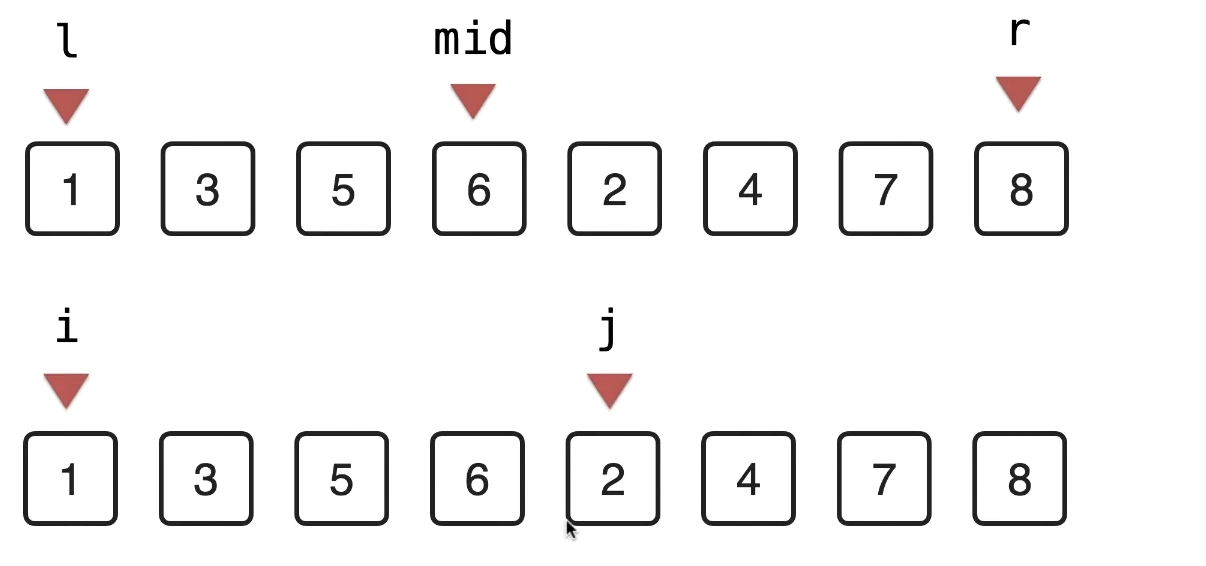
-
使用i j 两个索引 对比,result 直接写入原区间
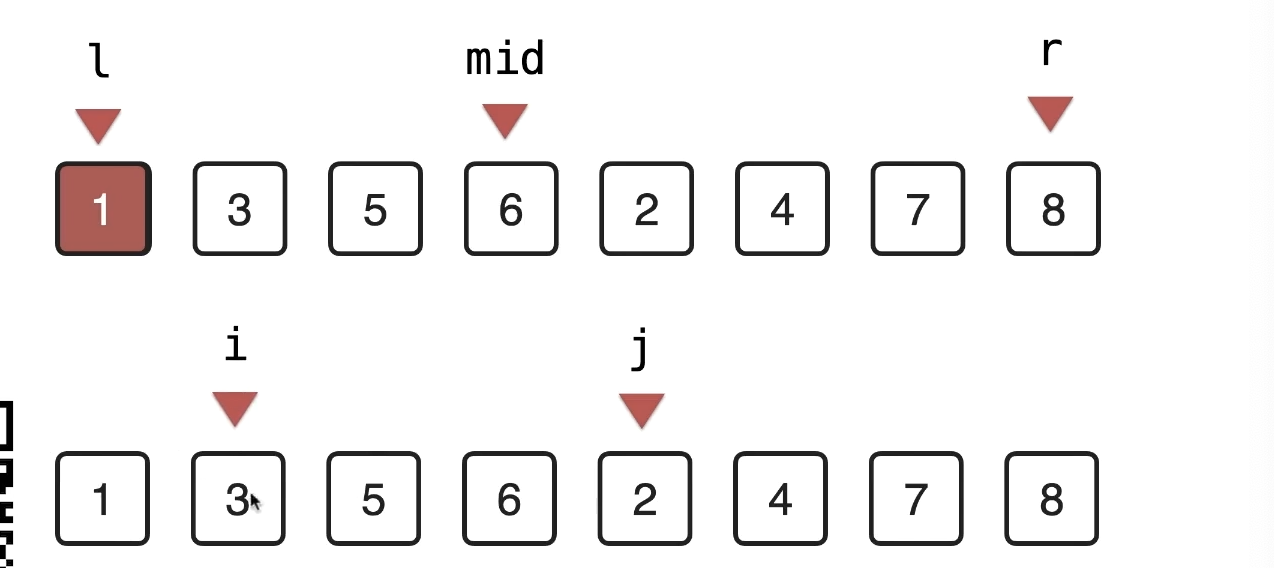
-
终止条件:i >= mid , j > r
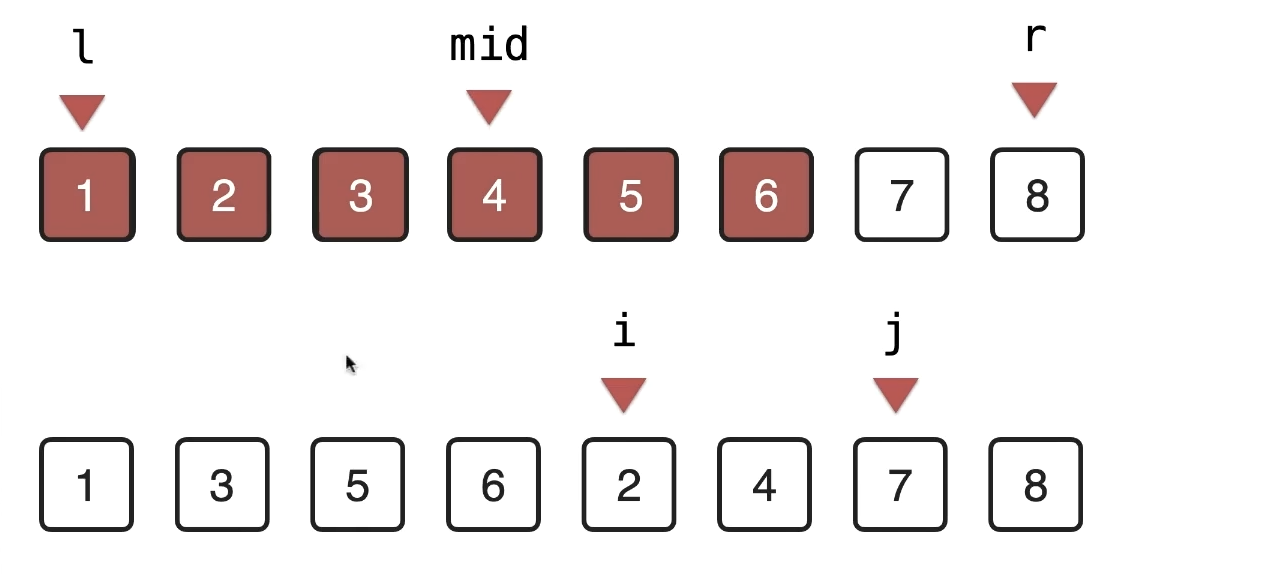
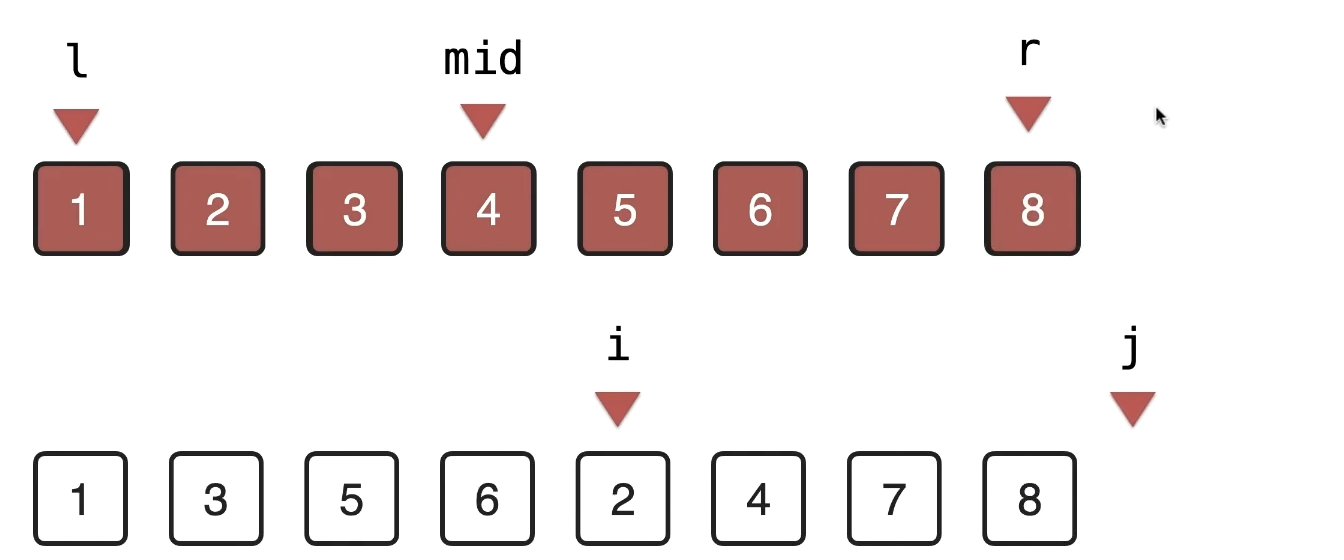
归并排序过程无法原地完成
1.5 归并复杂度分析
空间复杂度:由于需要 copy 一份出来,所以是O(n)
时间复杂度:
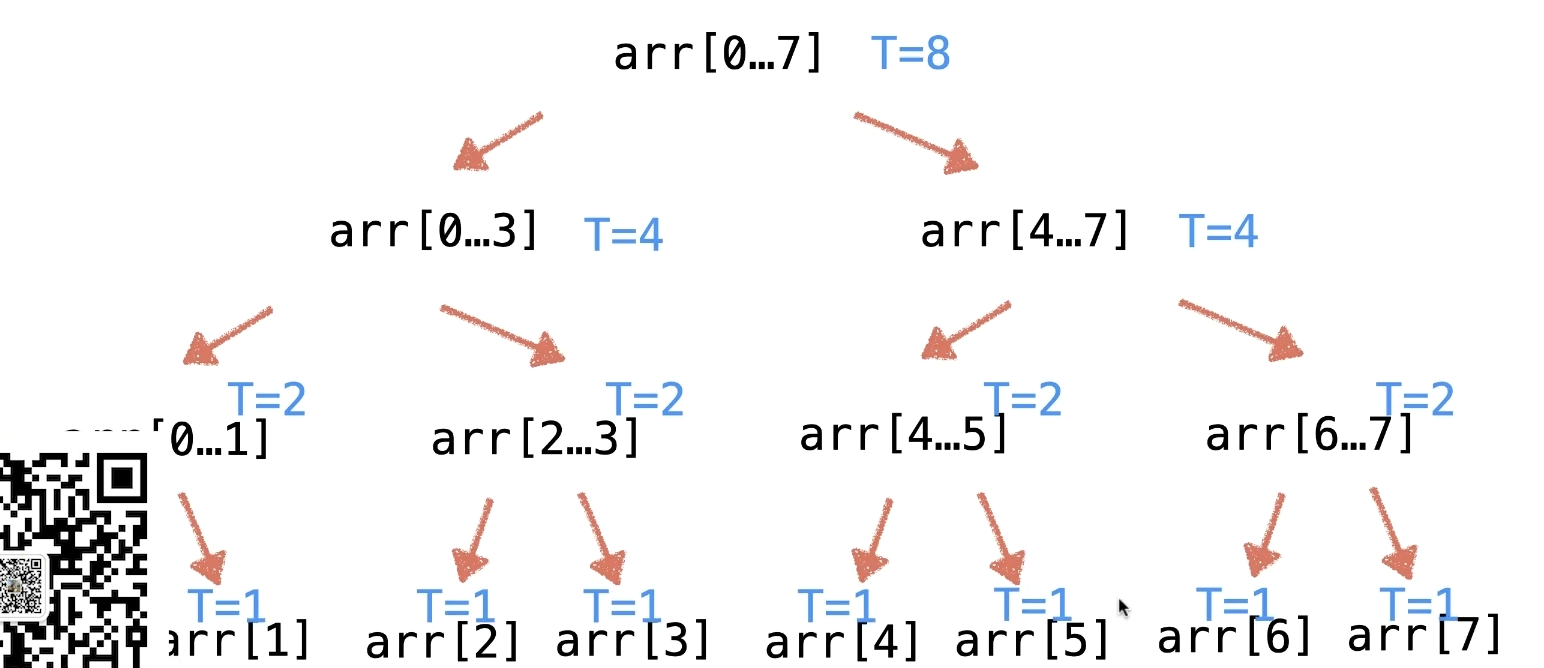
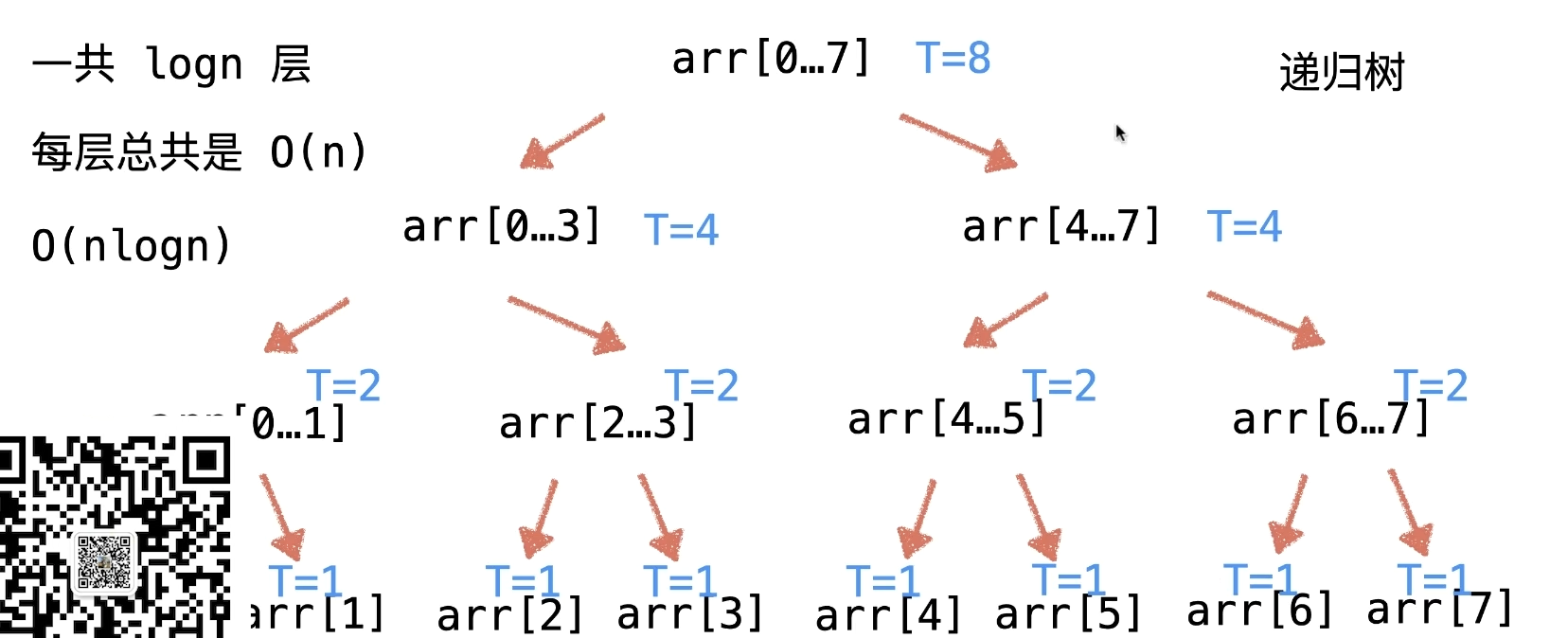
MergeSort:每一层总和都会有 n
一共有 logn层
所以是O(n logn)
二、希尔排序
冒泡排序每次只能一位
希尔排序希望 很大的元素能够很快的移动到最后面
2.1 希尔排序思想
-
距离为4 (n/2)分组

-
每一组内,元素进行插入排序

完成一轮组内的插入排序之后

-
距离为2 (n/4)分组

-
再次组内插入排序

-
距离为(n/8)的排序
由于只有8个,所以也就是array本身
全体进行插入排序

2.2 为什么中间要用插入排序
希尔排序经过前面的分组内排序之后,
数组已经大体上都是有序的了
插入排序只需要找到前面一个不小于的即可
因此 最后 插入排序会省一些前面的比较步骤

2.3 希尔排序的复杂度

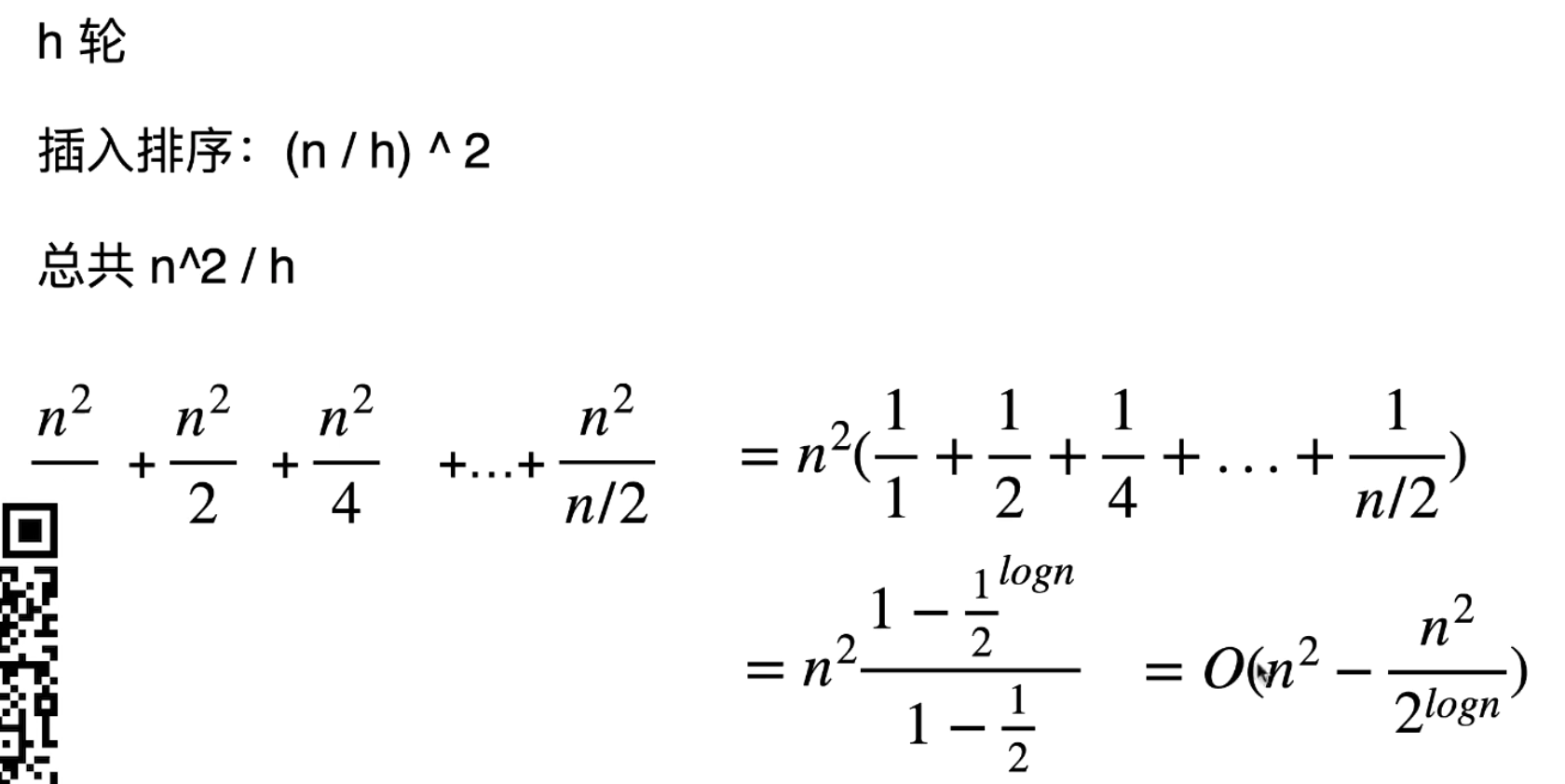
因此也称为 O(n^1.5)