目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1、基本原理
4.2、数学公式
4.3、实现过程
5.算法完整程序工程
1.算法运行效果图预览
2.算法运行软件版本
matlab2022a
3.部分核心程序
................................................................
load data.mat
N_tarray = 3; % 定义发射阵列元素数量
N_rarray = 4; % 定义接收阵列元素数量
Pulses_t = 64; % 定义脉冲数量
fcarrier = 7.9e10; % 定义载波频率
fsample = 1e7; % 定义ADC采样频率
Tc = 2.56e-5; % 定义线性调频或扫描的持续时间
Bw = 1e9; % 定义线性调频或扫描的带宽
S_rarray = 0.0019; % 定义接收阵列元素间距
c = 3e8; % 定义光速
lambda = c/fcarrier; % 根据载波频率计算波长
Rd = c / (2*Bw); % 计算距离分辨率
N = Tc * fsample;% 计算每个线性调频或扫描的快速时间采样数量% 以下是数据处理部分,将原始数据转化为虚拟阵列矩阵
Data1 = func_arraycube(Data);
% 获取第一个拍频信号
Xvr = squeeze(Data1(:, 32, :));
% 计算采样点数量
N_s1 = N_tarray * N_rarray * 128;
N_s2 = N * 2;
% 计算S1的采样点
S1_samp = -pi / 2 : pi / N_s1 : pi / 2 - pi / N_s1;
% 计算S2的采样点
S2_samp = (0 : N_s2 - 1) * Rd * N / N_s2;
% 计算S0的采样点
S0_samp = -1 : 2 / N_s1: 1 - 2 / N_s1;
% 计算空间间距
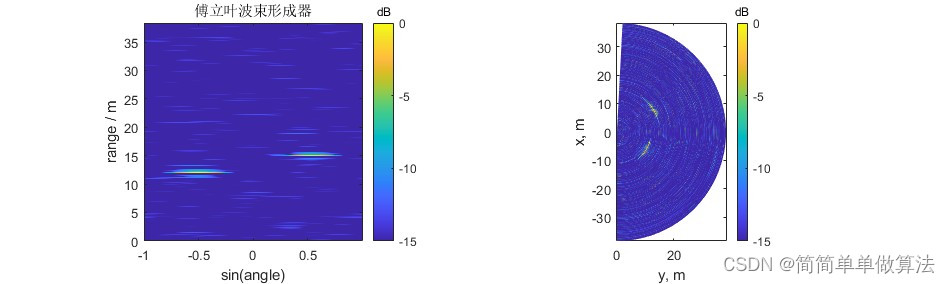
d_space = S_rarray / lambda;% 以下是波束形成器的使用部分,首先使用傅立叶波束形成器
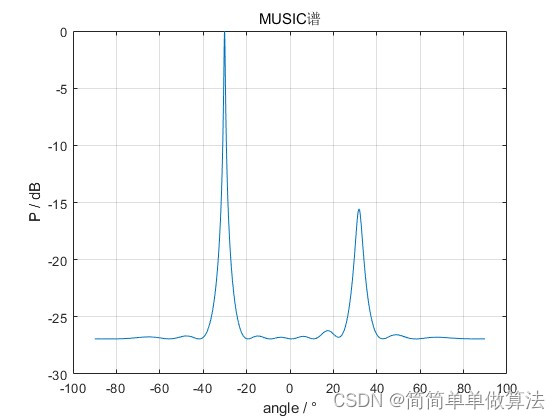
[~] = func_2Dfft(Xvr,S2_samp,S0_samp);% 然后使用MUSIC波束形成器
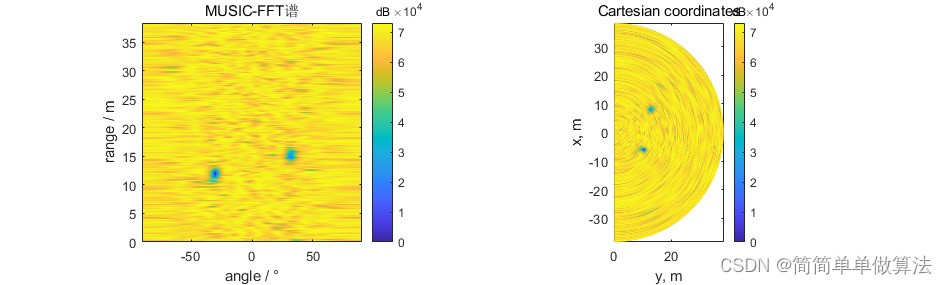
[~] = func_music(Xvr,S1_samp,d_space);% 最后使用fftMUSIC波束形成器
[~] = func_musicfft(Xvr,S2_samp,S1_samp,d_space);
68
4.算法理论概述
MUSIC (Multiple Signal Classification) 算法是一种广泛应用于信号处理领域的算法,它可以用于估计信号的波达方向或频率。在超声波成像中,MUSIC 算法可以用于提高图像的分辨率和降低噪声。基于MUSIC算法的二维超声波成像是通过使用超声波探头发射和接收超声波信号,然后利用 MUSIC 算法对接收到的信号进行处理,以得到高分辨率的图像。
4.1、基本原理
MUSIC 算法的基本思想是将信号数据分为两个部分:噪声和信号。通过建立信号子空间和噪声子空间,将信号投影到信号子空间,将噪声投影到噪声子空间。然后,利用信号和噪声在两个子空间中的投影系数不同,求出信号的方向或频率。
在二维超声波成像中,MUSIC 算法可以将超声波信号视为信号,将噪声和其他干扰视为噪声。通过建立信号子空间和噪声子空间,将接收到的信号数据投影到两个子空间中,并计算出信号的方向或频率。然后,利用这些方向或频率信息,可以得到高分辨率的图像。
4.2、数学公式
设超声波信号为 s(t),则可以通过以下公式表示 MUSIC 算法的输出:
P(f) = 1/(N-1) * sum(S(f)/(S(f) + N(f)))
其中,f 是频率,S(f) 是信号在频率 f 处的功率谱密度,N(f) 是噪声在频率 f 处的功率谱密度,P(f) 是 MUSIC 谱。
在二维超声波成像中,可以将 P(f) 作为像素值,绘制出高分辨率的图像。如果 P(f) 的值较大,则说明在该频率处有信号存在,否则说明没有信号存在。因此,通过计算 P(f) 的值,可以得到高分辨率的图像。
4.3、实现过程
基于 MUSIC 算法的二维超声波成像的实现过程如下:
- 数据采集:使用超声波探头发射和接收超声波信号,并将接收到的信号存储在计算机中。
- 数据预处理:对接收到的数据进行预处理,例如去除直流分量、增益控制、滤波等。
- 数据分帧:将预处理后的数据按照时间顺序分为一帧一帧的数据。
- 建立信号子空间和噪声子空间:利用一帧数据可以建立信号子空间和噪声子空间。首先,对一帧数据进行特征值分解,得到特征值和特征向量。将特征值按照从大到小的顺序排列,前几个大的特征值对应的特征向量就是信号子空间的基向量,其他特征值对应的特征向量就是噪声子空间的基向量。
- 计算 MUSIC 谱:利用上一步得到的信号子空间和噪声子空间基向量,可以计算出 MUSIC 谱。具体方法是,将接收到的信号数据投影到信号子空间和噪声子空间中,并计算出信号的方向或频率。然后,利用 MUSIC 算法的公式计算出 MUSIC 谱。
- 成像:将 MUSIC 谱作为像素值,绘制出高分辨率的图像。可以将像素值进行可视化处理,例如映射为灰度值或彩色值。
- 数据后处理:对绘制出的图像进行后处理,例如滤波、增益控制、图像拼接等。
需要注意的是,MUSIC 算法对噪声较为敏感,因此在进行数据处理之前需要先进行数据预处理和数据分帧。另外,在实现过程中需要使用大量的矩阵运算和数值计算,因此需要使用高性能的计算设备和优化算法来提高计算效率。
5.算法完整程序工程
OOOOO
OOO
O