往期文章：解决0-1背包问题（方案一）:二维dp数组_呵呵哒(￣▽￣)"的博客-CSDN博客
https://blog.csdn.net/weixin_41987016/article/details/133207350?spm=1001.2014.3001.5501
>>探索一维dp数组和二维dp数组的本质
>>思考
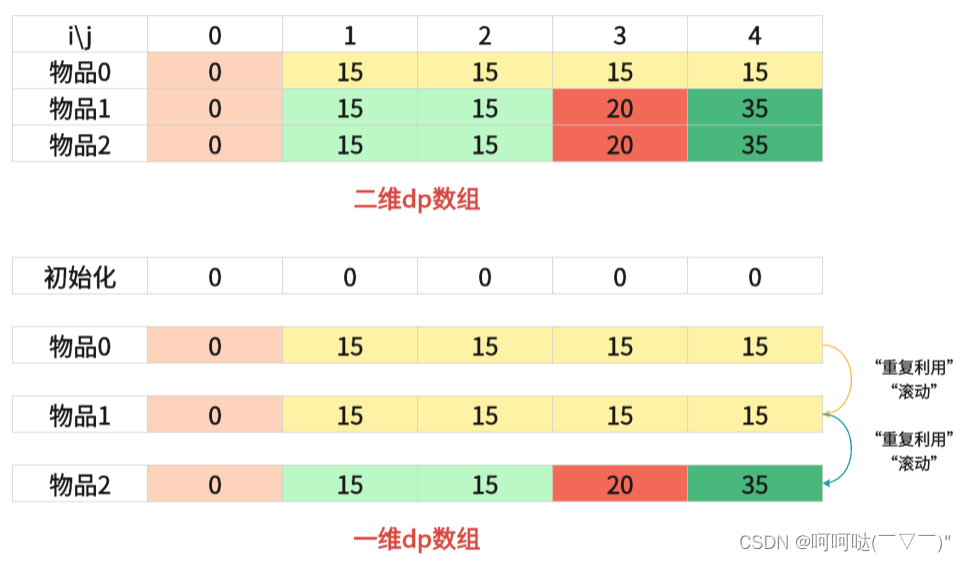
- 理解整体上是如何从二维降为一维的，理解何为滚动数组？
当前层是由上一层推导出来的，那么我们直接就把上一层拷贝到当前层，直接在当前层进行计算。把新的值覆盖到当前层之中。然后下一轮计算的时候。再从当前层取值，然后再计算新的值再覆盖当前层。这样就相当于把一个矩阵压缩成一行数据。每一次计算都更新这一行数据，那看起来就像是在滚动更新这个数据。所以说我们称之为滚动数组，把一个二维的dp数组降为一维dp数组。
>>总结
1.对于背包问题其实状态都是可以压缩的
2.在使用二维数组的时候，递推公式:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
3.可以发现若把dp[i-1] = max(dp[i][j],dp[i][j-weight[i]] + value[i]);
也就是说与其把dp[i-1] 这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）
4.滚动数组，需要满足的条件是上一层可以重复利用，直接拷贝到当前层
>>>>>>>>>>>>>>>>>>>>>>>>进入正题>>>>>>>>>>>>>>>>>>>>>>>>
>>动规五部曲：
1.确定dp数组的定义
在一维dp数组中，dp[j]表示:容量为j的背包，所背的物品价值可以最大为dp[j]
2.一维dp数组的递推公式
dp[j] 为容量为j的背包所背的最大价值，那么如何推导 dp[j] ?
- dp[j] 可以通过dp[j-weight[j]] 推导出来，dp[j-weight[i]] 表示容量为 j-weight[i] 的背包的最大价值
- dp[j-weight[i]]+value[i] 表示容量为 j - 物品i重量的背包 加上 物品i 的价值，即容量为j的背包，放入物品i了之后的价值为dp[j]
- dp[j]有两个选择，一个是取自己dp[j]，一个是取 dp[j-weight[i]] + value[i]，指定是取最大的，毕竟是求最大价值
3.一维dp数组如何初始化
关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候会越来越乱
dp[j]表示:容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该就是0，因为背包容量为0所背的物品的最大价值就是0
>>思考
- 那么dp数组除了下标0的位置，初始为0，其他下标应该初始化为多少呢？
递推公式:dp[j] = max(dp[j],dp[j-weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数，若题目给的价值都是正整数，那么非0下标都初始化为0就可以了。若题目给的价值有负数，那么非0下标就要初始化为负无穷。
>>目的
- dp数组在递推公式的过程中取的最大的价值，而不是被初始值覆盖了
4.一维dp数组遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}背包的倒序遍历是为了保证 物品i 只被放入一次！
5.推导dp数组
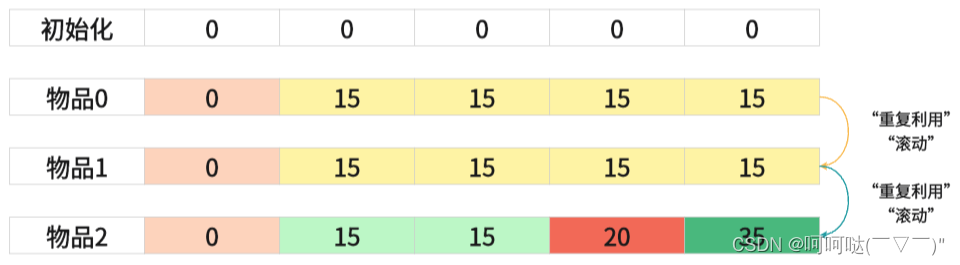
>>详细讲解
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
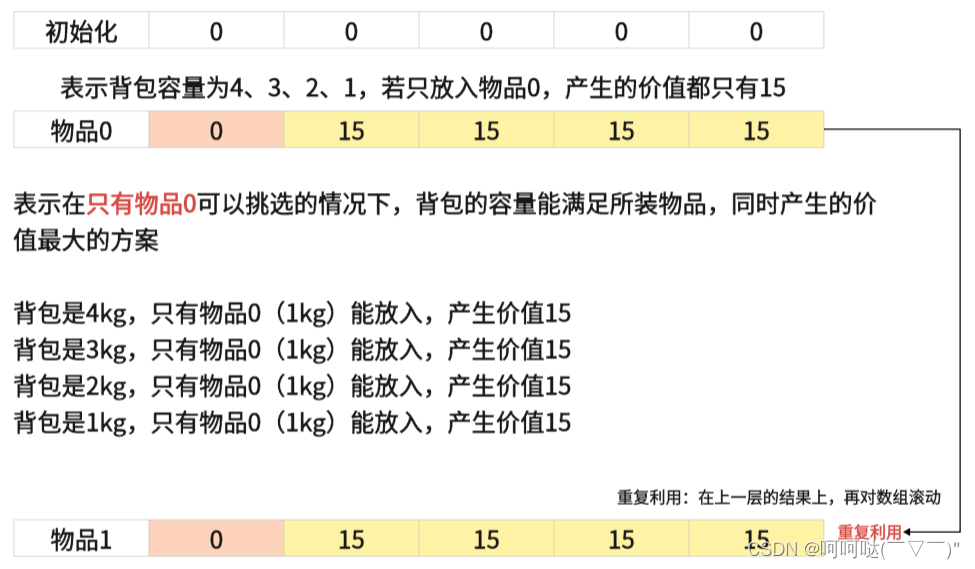
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
完整代码：
#include <iostream>
#include <vector>
using namespace std;// 一维dp01背包完整C++测试代码
void test_1_wei_bag_problem() {vector<int> weight = { 1,3,4 };vector<int> value = { 15,20,30 };int bagWeight = 4;// 初始化vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < weight.size(); i++) {for (int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_1_wei_bag_problem();
}
