本人最近在研究一款针对青少年儿童的教育游戏，希望从培养孩子各方面的综合素质出发，引导孩子掌握多方面的软知识，软技能。其中有一个比较新颖的游戏玩法------打猎。该玩法创新点在于，引入了食物链的概念。过去一般的游戏里，打猎场景里面的动物都是源源不断。这跟现实生活严重脱节。我研发的这个小游戏，希望能通过参考现实生活的生态系统功能，既能保证每种动物能以一定的繁殖速度增加种群数量，也会因为被天敌或者玩家猎杀，而导致数量紧剧下降，最终导致整个生态系统崩塌。通过这样的设定，来教育小朋友要保护好我们的生态环境。

既然涉及到食物链，一个不得不提的问题是，天敌与下游动物此消彼长的数量关系。一个很自然的想法就是，只要下游动物的繁殖速度足够快，大于天敌自身种群数量以及其增长速度。种群的数量应该是比较平稳的。但事实上是这样的吗？

下面是我的一组测试数据，我模拟了兔子和老虎种群数量的对应关系。假设兔子的种群数量为120，老虎的种群数量为10，兔子和老虎的繁殖率均为1.1。每只老虎每天都要吃一只兔子。按道理每天兔子新增的数量都会比老虎的数量加新增数要多。从上面的推测来看，兔子的数量应该是平稳的。但实测结果是：

第1天：当前兔子120.0只，老虎10.0只，相差110.0只

第2天：当前兔子121.0只，老虎11.0只，相差110.0只

第3天：当前兔子121.0只，老虎12.0只，相差108.0只

第4天：当前兔子119.0只，老虎13.0只，相差106.0只

第5天：当前兔子117.0只，老虎14.0只，相差102.0只

第6天：当前兔子112.0只，老虎16.0只，相差96.0只

第7天：当前兔子106.0只，老虎17.0只，相差88.0只

第8天：当前兔子97.0只，老虎19.0只，相差77.0只

第9天：当前兔子85.0只，老虎21.0只，相差64.0只

第10天：当前兔子70.0只，老虎23.0只，相差47.0只

第11天：当前兔子51.0只，老虎25.0只，相差25.0只

第12天：当前兔子28.0只，老虎28.0只，相差0.0只

上面的数据中免子当天的数量=（免子上一天的数量 – 老虎上一天的数量）*繁殖率。为了数据精确，动物的数量都使用浮点数。只是打印的时候，以下取了个整，实测结果表明，虽然兔子撑过了两轮攻击，但随着老虎数量的持续上升，兔子的数量开始出现了明显的下滑。

这证明之前的思路有问题。但到底怎么设计这个增长速度才比较合理？众所周知，计算机能处理的数据是有限。如果疯狂给兔子叠繁殖BUFF，兔子的数据很快就会溢出（指数爆炸）。那么，怎么定这个增长速度才比较合理呢？这就需要借助数学的力量。

首先，我们必须给上述场景来个数学建模。上面的问题是一个经典的迭归函数定义。为了数学推导的通用性，假设兔子的初始数量为a,繁殖率为q,老虎的数量为b，繁殖率为p，容易得出关于兔子数量的迭推公式:

现假定F(0)=a，

F(x)= ( f(x - 1) – b * p ^ （x – 1） ) * q

现在我们希望兔子至少能存活x天。即f(x)>0.

∵ qa >0

∴ f(x – 1) > b * p ^ (x - 1)

换下元有：f(x) > b* p ^ x

下面我们尝试把迭推公式展开，我们留意到

f(1)=(a-b) * q

f(2) = ((a – b) * q – b * p ) * q

= (a * q – b (q + p)) * q

f(3) = ((a * q – b (q + p )) * q – b * p ^ 2) * q

     = (a * q ^ 2 – b( q ^2 + q * p + p ^ 2)) * q

……

由此，一个大胆的想法就出来了，根据上述规律，兔子种群函数会不会是:

fx=a* qx-1-b*i=1xqx-ipi-1*q    （1）

下面使用数学归纳法证明，设有f(k)为

fk=a* qk-1-b*i=1kqk-ipi-1*q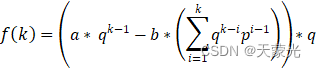

由迭推公式得f(k + 1)

fk+1=fk-b*pk*q

将f(k)的展开式代入得

fk+1=a* qk-1-b*i=1kqk-ipi-1*q-b*pk*q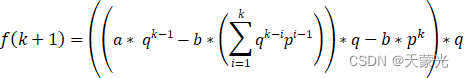

简单处理下，即得：

fk+1=a* qk+1-1-b*i=1kqk+1-ipi-1+ pk*q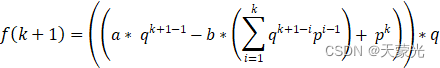

通过观察，容易发现最里层括号里的第1项，则好是

ik+1qk+1-ipi-1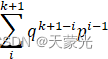

的前k项，而第2项刚好是上式的最后一项。因此合并后即得

fk+1=a* qk+1-1-b*i=1k+1qk+1-ipi-1*q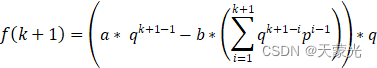

满足我们猜想的形式，命题得证！f(x)的迭推公式展开式即为（1）式

留意到（1）式最内层的括号的累加式，实为首项q ^ x - 1，公比为p/q的等比数列的累加和。由等比数列的求程公式即得进一步化简后的公式(m=p/q)

fx=qx*(a-b* mx-1m-1)   (2)式

上机测试一下，令兔子开始的数量为a = 100，老虎的数量为b=10，兔子增殖率q = 4,老虎增殖率为 p=2。得到如下结果。

n=10.0,a=100.0,q=4.0,b=10.0,p=2.0

第1天：当前兔子100.0只，老虎10.0只，最后剩90.0只,扩展式计算结果:100.0

第2天：当前兔子360.0只，老虎20.0只，最后剩340.0只,扩展式计算结果:360.0

第3天：当前兔子1360.0只，老虎40.0只，最后剩1320.0只,扩展式计算结果:1360.0

第4天：当前兔子5280.0只，老虎80.0只，最后剩5200.0只,扩展式计算结果:5280.0

第5天：当前兔子20800.0只，老虎160.0只，最后剩20640.0只,扩展式计算结果:20800.0

第6天：当前兔子82560.0只，老虎320.0只，最后剩82240.0只,扩展式计算结果:82560.0

第7天：当前兔子328960.0只，老虎640.0只，最后剩328320.0只,扩展式计算结果:328960.0

第8天：当前兔子1313280.0只，老虎1280.0只，最后剩1312000.0只,扩展式计算结果:1313280.0

第9天：当前兔子5248000.0只，老虎2560.0只，最后剩5245440.0只,扩展式计算结果:5248000.0

第10天：当前兔子2.098176E7只，老虎5120.0只，最后剩2.097664E7只,扩展式计算结果:2.098176E7

完美！证明展开式是对的。

有了(2)式，就可以回到前面的讨论，如何令f(x) > 0。

∵ q > 0

∴ a>b* mx-1m-1

这里针对m可能的值，分开讨化。

当p > q时，m >１，m^x随着ｘ变大，不等式右边是一个迭增函数。因此，不等式终究会不成立。

如果p < q, m < 1，

不等式变换为：

a>b* 1-mx1-m

m^x随着ｘ变小，１－ｍ＾ｘ的值增大，不等式右边还是一个迭增函数。因为０＜m^x＜１。所以只需要保证ａ＞＝ｂ／（１－ｍ）。就可以保证兔子永远不会被灭绝

有了上述数学结论，游戏里面就只需要设置好兔子的增殖率和老虎的数量，增殖率，就可算出兔子的初始种群ａ，使其一定不会灭绝。同时，也可以通过调整增殖率让动物的数量保持在一定范围，不会导致程序数据溢出。游戏整个生态系统的稳定性就有了理论上的保障。