题目:
96. 不同的二叉搜索树
中等
2.4K
相关企业
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
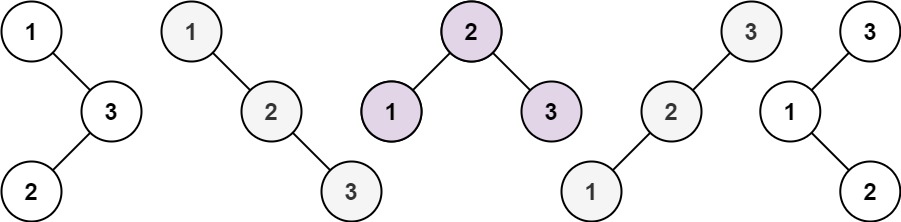
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 19
思考历程与知识点:
来看看n为3的时候,有哪几种情况。
当1为头结点的时候,其右子树有两个节点,和 n 为2的时候两棵树的布局是一样的!
(可能有同学问了,这布局不一样啊,节点数值都不一样。别忘了我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式。
思考到这里,这道题目就有眉目了。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
- 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ,都是一样的。
以下分析如果想不清楚,就来回想一下dp[i]的定义
- 确定递推公式
在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
那么dp[0]应该是多少呢?
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1
- 确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历。
代码如下:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}
题解:
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};欢迎点赞,收藏,评论,你的鼓励就是我创作的最大动力!(๑╹◡╹)ノ"""
版权声明:本文为CSDN博主「渡梦酒」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:渡梦酒的博客_CSDN博客-csdn领域博主