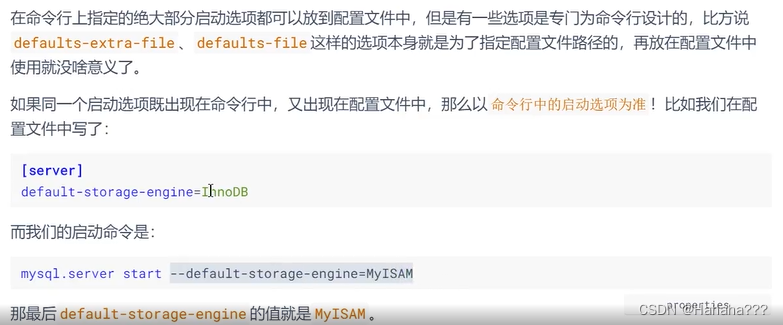
目录
题目
样例
题目解析
代码
图解
矩形相交
题目
输入2个矩形的左上角和右下角两个点的坐标值(x,y),判断2个矩形是否相交,输出YES或者NO。矩形的边应与x,y轴相平行。假定输入坐标能顺利构成矩形,不考虑无效矩形的况
难度:白银
格式:
输入格式:输入整型,空格分隔。 每行输入一组信息。
输出格式:输出YES或者NO
题目链接 :矩形相交
样例
输入: -20 20 20 -10 -10 10 10 -5 输出: NO
备注:特殊情况考虑:在数学中,两个图形相交是指它们有公共的部分,或者说同时属于两者的点的集合不是空集。若两个几何图形在某个地方有且只有一个交点,则可以称为相切而不是相交。即,在此题中,两矩形只有一交点视为相切,有一条边完全或者部分重合视为相交。两矩形完全重合,视为重合不是相交
题目解析
矩形相交,思路是先考虑特殊情况 。根据输入的是 左上和右下的坐标
- 两个矩形完全重合的时候,该题判为重合而 不是相交。
- 两个矩形只有一个点相交,该题即判为相切而 不是相交
- 两个矩形没有任何交集, 不是相交
代码
#include<stdio.h>
#include<math.h>
int main()
{int x1, y1, x2, y2, x3, y3, x4, y4;scanf("%d %d %d %d\n%d %d %d %d", &x1, &y1, &x2, &y2, &x3, &y3, &x4, &y4);if(x1==x3&&y1==y3&&x2==x4&&y2==y4)//重合不是相交{printf("NO");return 0;}else if( (x2==x3&&y2==y3) || (y1==y4&&x2==x3) || (y3==y2&&x4==x1) || (x4==x1&&y4==y1))//相切不是相交{printf("NO");return 0; }else if(( x1<x3&&x4<x2&&y4>y2&&y1>y3 ) ||(x3<x1&&x2<x4&&y2>y4&&y3>y1))//包含不是相交{printf("NO");return 0; }else if(x1>x4||x2<x3||y1<y4||y2>y3){//两个矩形的相对位置 左右上下printf("NO");return 0; }elseprintf("YES");return 0;
}
图解
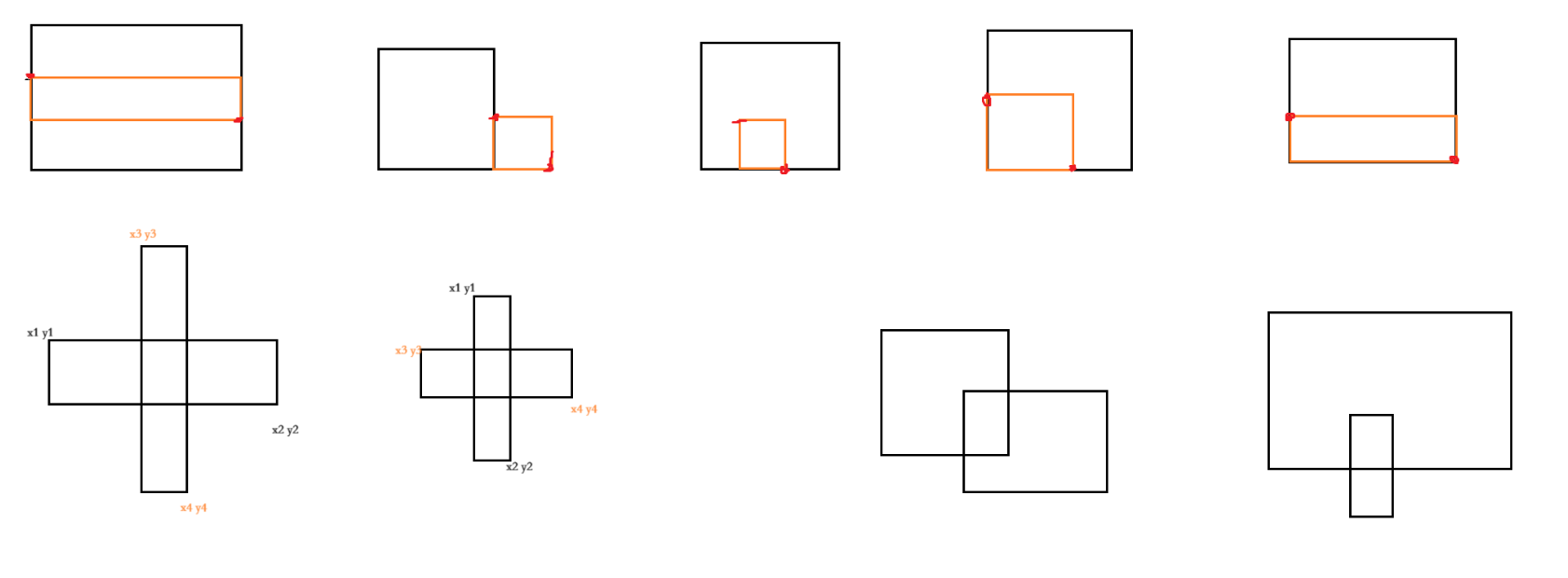
下面列出的是不相交的图案 ,当把所有不相交的情况列出,剩余的就是相交的
- 两个矩形重合

x1==x3&&y1==y3&&x2==x4&&y2==y4 - 相切(相交于一点)
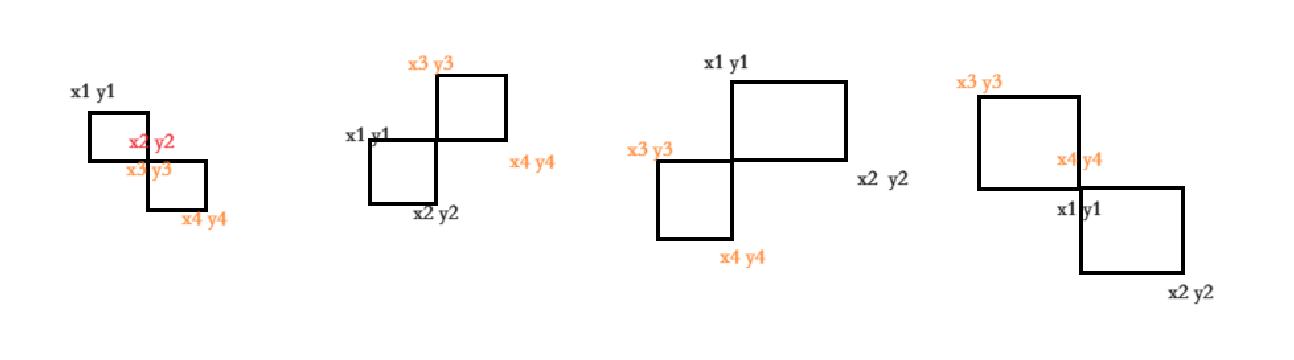
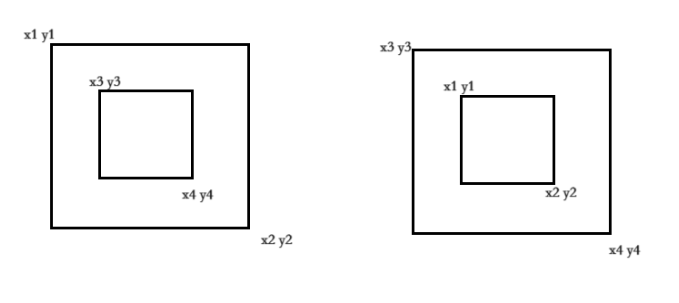
(x2==x3&&y2==y3) || (y1==y4&&x2==x3) || (y3==y2&&x4==x1) || (x4==x1&&y4==y1) - 嵌套
( x1<x3&&x4<x2&&y4>y2&&y1>y3 ) ||(x3<x1&&x2<x4&&y2>y4&&y3>y1)
- 相对位置 左右上下
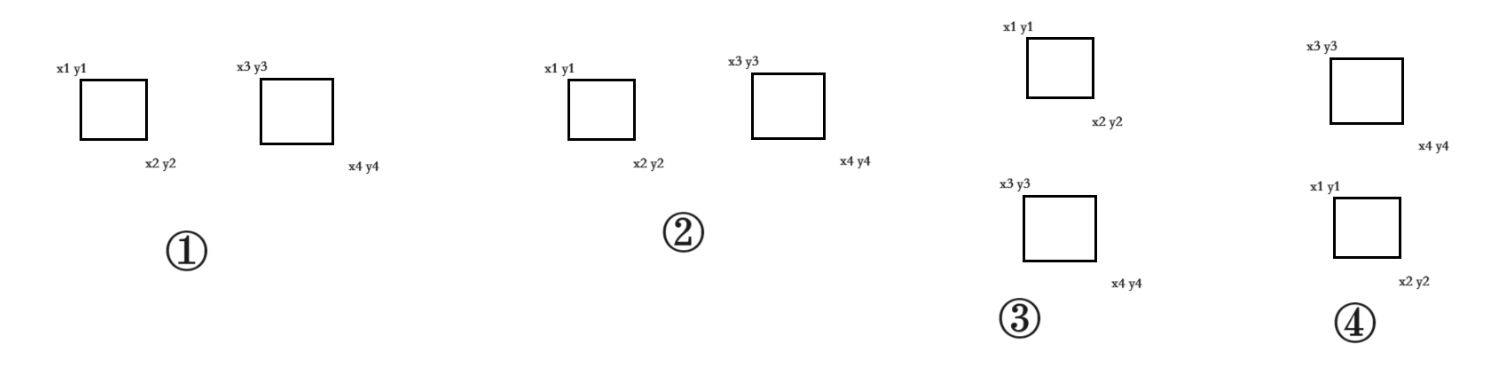
x1>x4||x2<x3||y1<y4||y2>y3
注意上述是矩形不相交的情况
矩形相交
矩形相交还有其他解法 就是比如 直接把所有矩形的相交的情况全部列出来,然后找规律(提示 点在线上)
下面是矩形相交的情况