(链接:从零开始之电机FOC控制_foc电机_一只小白啊的博客-CSDN博客)之后,总感觉整个流程都知道,但是深入到具体细节时,就不知所措,感觉啥也不懂一样。
那么为什么要用FOC控制无刷电机呢?要知道这个问题,就要先从无刷电机的工作特性开始了解(即电机工作本质),然后再针对电机工作特性设计出了基本驱动(按照有刷电机方式驱动,即六步换向法),再优化驱动控制得到了相对较优秀的控制方法即FOC(细化工作逻辑,包含坐标转换和空间矢量PWM)。
于是乎有了这一系列《从零开始之了解电机及其控制》,只有知道了电机的特性才能更好的去驱动它。咱们废画不哆嗦,直接开干。
引导问题:磁场的本质是啥?为什么马达/电机需要用电驱动呢?
大家应该都玩过磁铁,具有同性相斥、异性相吸的特性,这个特性本质是磁场的相互作用产生的。
磁场特性应用(磁场对准):当将磁铁放在外部磁场中,磁铁的N极受力方向与磁场方向相同,S极受力方向与磁场方向相反,直到达到磁极与磁场方向一致的平衡状态。如指南针。
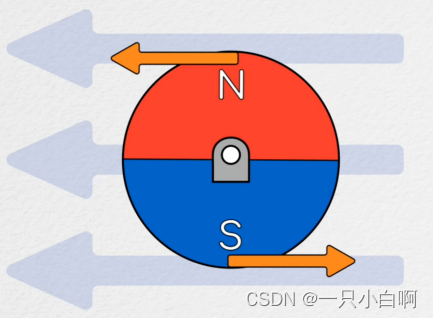

磁场是磁铁发出的矢量场,本质是材料中带电粒子的同步旋转运动引起的。


那么平移的带电粒子是否也会产生磁场呢?是的,有序移动的带电粒子可以产生磁场。
导体中的自由电荷在电场力的作用下做有规则的定向运动就形成了电流,这种定向运动的方向也就是电流方向,规定正电荷运动的方向为电流方向。电流的本质是单位时间穿过材料横截面的电荷数量。

如果电流流过一根导线,那么就可以认为该导线中的电荷在电流方向上具有一定的速度。


安培定则一:用右手握住通电直导线,让大拇指指向直导线中电流方向,那么四指指向就是通电导线周围磁场的方向;

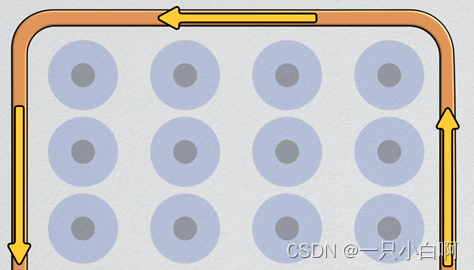
下图所示的×表示方向向内·表示方向向外。

将导线围成一个圈,并让电流流过,那么圈内的磁场将会成倍增加,如下图逆时针的电流将使线圈内部产生指向外的磁场。
由安培定则一可知,移动带电的粒子可产生磁场。那如果在一个磁场中移动带电粒子会产生什么现象?由磁场的相互作用,我们知道它会收到一个力的影响,这个力叫洛伦兹力。
F = q(E + vB )= q E + qvB
F是洛伦兹力,q是带电粒子的电荷量,E是电场强度,v是带电粒子的速度,B是磁场磁感应强度,注意这里F、E、v和B都是向量。
qE表示,如果带电粒子处于电场中,它将受到与电场强度和粒子的电荷量成正比的力,力的方向沿着电场的方向。
qvB表示,如果带电粒子穿过磁场,它将受到一个与磁场强度、粒子的电荷量、运动速度成正比的力,力的方向垂直于磁场平面和速度平面。

当有大量电荷粒子通过时,这就会产生了实质性的力。
例如,当有一条通电导线存在于与电流不平行的外部磁场中,那么每个电荷都会受到磁场施加在上净力,由此可得安培力公式F = IL x B,F是安培力、I是电流、L是导线长度、B是磁场强度,注意这里F、I、L、B都是向量,x是叉积。

从而我们可以将电流转化为机械运动即电能转换为机械能,如果把这个想法运用在闭合的导线上,一个有电流的方形导线环路,把它放在磁场中,左边的导线电流向内,在磁场中受到的作用力向下,右边的导线电流向外,在磁场中受到的作用力向上。

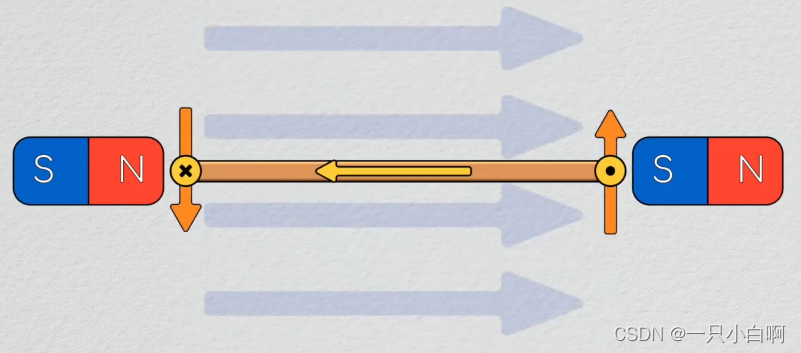
由于两个力方向相反,会在线圈上产生净扭矩,使线圈旋转,最终达到平衡状态。这里的扭矩τ是受力边的长度r与力F的叉积。

因此,导线环上的扭矩量等于导线直径与ilB结果的叉积,于是乎我们得到了磁场中载流导线环上的扭矩方程。

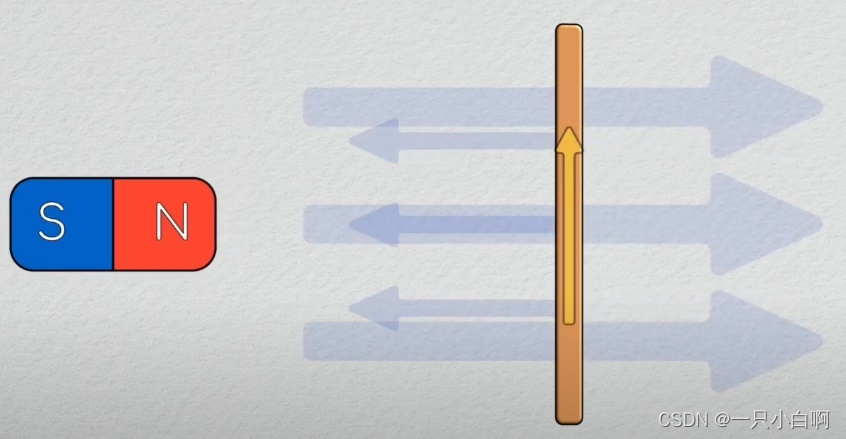
在继续学习电机如何工作之前,还需要了解一个重要的定律:电磁学的一条基本定律,法拉第定律(法拉第电磁感应定律):任何封闭电路中感应电动势大小,等于穿过这一电路磁通量的变化率。ε是电动势,单位为伏特,ΦB是通过电路的磁通量,单位为韦伯。本质上是说磁通不能变化太快,如果外部磁场发生变化,环路就会产生电动势,从而使电流在环路中流动同时感应出一个磁场,改磁场抵抗变化的磁通量。

例如,如果外部磁场强度增加,导线内部就会感应出一个磁场,该磁场与外部磁场方向相反,如果外部磁场强度减小,导线内部就会感应出与一个与外部磁场方向相同的磁场。

这个定理对于后续理解电机的的动态特性很重要!
如下图,线圈从垂直状态变化时,穿过环路的磁通量减小,就会导致线圈产生一个磁场抵抗这种减小,从而在线圈中产生电流。


线圈从水平状态变化时,穿过环路的磁通量增加,就会导致线圈产生一个磁场抵抗这种增加,从而在线圈中产生电流。


附录:
1、安培定则二:用右手握住通电螺线管,让四指指向电流的方向,那么大拇指所指的那一端是通电螺线管的N极。

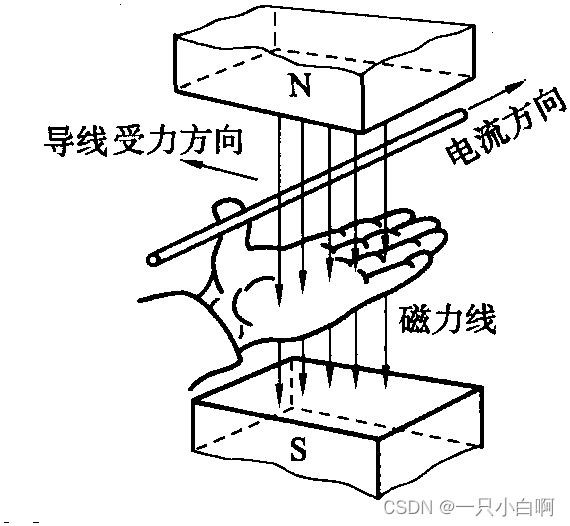
2、左手定则:将左手掌摊平,让磁感线穿过手掌心,四指表示电流方向,则和四指垂直的大拇指所指方向即为洛伦兹力的方向。
3、《了解电机》这一系列都是根据youtuber(Jantzen Lee)的视频而写的,也可直接去看原视频。