题目：

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

示例 1:

输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。

示例 2:

输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

提示：

• 1 <= nums.length <= 105
• nums[i] 不是 0 就是 1

算法原理：

题目要求找出⼀段连续的区间，其中0和1出现的次数相等

如果将0转成-1，1还是1，题目就转化成找出最长的⼀段区间，且这段区间的和等于 0

前缀和算法就可以快速求出某一区域内所有元素的和

枚举所有子数组可以每次固定起始的位置，依次向后枚举，所以我们当然可以每次固定末尾的位置，依次向前枚举

i是每次固定的末尾位置，从i位置开始依次向前枚举可以枚举出i位置开始的所有子数组，题目要求最长的且和为0的区间，所以我们每次只需要选出i位置开始所有子数组中满足要求的最优子数组即可，标准就是：在[0,i-1]的区间内找到第一次出现sum的位置j，i-j就是本轮i位置能够枚举的所有子数组中满足要求的最优（最长）子数组

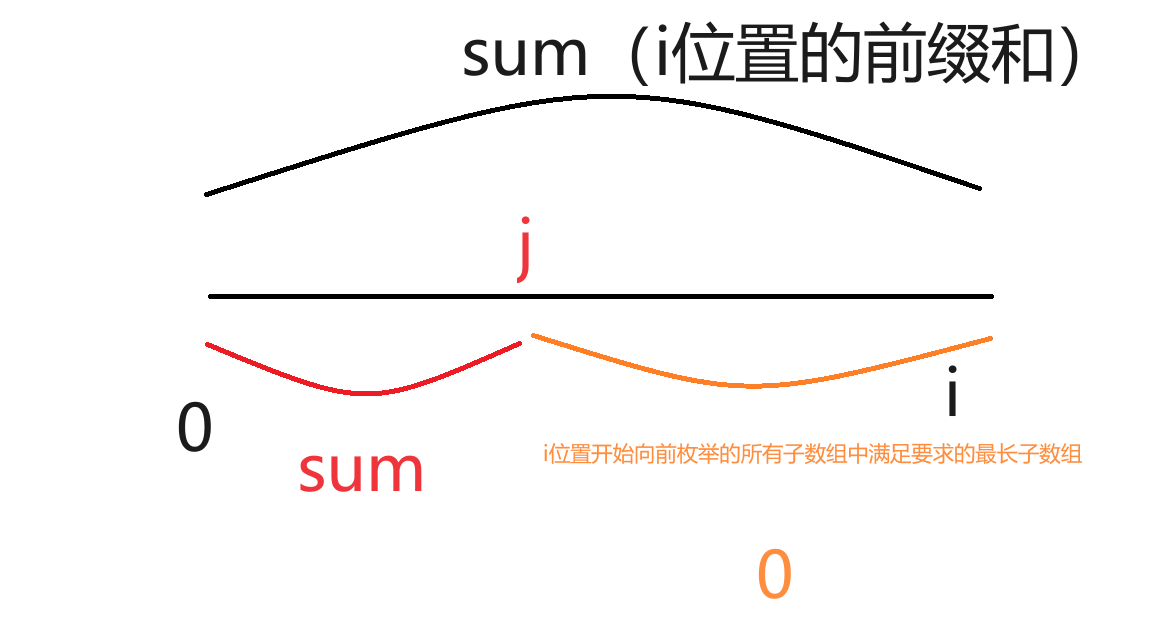
前缀和+哈希表：

哈希表记录前缀和出现的位置 （只记录每个前缀和第一次出现时的位置）

1 计算出当前位置的前缀和 

2 在[0,i-1]（即前面的区域内）寻找第一次出现的前缀和为sum的位置j ，因为每轮都要寻找以i位置开始向前枚举的所有子数组中满足条件的最长子数组，也就是长度i-j，若是寻找的不是第一次出现的前缀和为sum的位置，那么长度i-j相较于原始的i-j只会减小，不会是最优解子数组的长度

3 判断是否需要记录当前前缀和为sum的位置

   若是当前位置的前缀和是第一次出现，则记录它此时的位置

   若不是第一次出现，则无需记录了，因为在前面已经有了sum了，且那个位置的sum一定比现在位置的sum靠前，且我们要求的是最长连续子数组，每轮能够枚举的所有子数组中满足条件的最长子数组长度是i-j，所以j越靠前越好

4 细节：

当前位置的前缀和若为0，即[0,i]的整个区域就是本轮i位置所有枚举出的子数组中和为0的最长子数组，长度为i-j，即前缀和为0时要记录的下标是-1，也就是j为-1

代码实现：

class Solution 
{
public:int findMaxLength(vector<int>& nums) {//问题转化为求和为0的最长子数组unordered_map<int,int> hash;//统计每个前缀和第一次出现的位置hash[0] = -1;// 默认有⼀个前缀和为 0 的情况int sum = 0;int ret = 0;for(int i = 0;i<nums.size();i++){sum+=nums[i]==0?-1:1;// 计算当前位置的前缀和if(hash.count(sum)){ret = max(ret,i-hash[sum]);}else{hash[sum] = i;}}return ret;}
};