利用 IMU 估计人体关节轴向和位置 —

Title: 利用 IMU 估计人体关节轴向和位置 —— “Joint axis and position estimation from inertial measurement data by exploiting kinematic constraints” —— 论文推导

文章目录

I. 论文回顾
II. 铰接关节的约束
- 1. 铰接关节约束的原理
- 2. 铰接关节约束的梯度
- 3. 铰接关节约束梯度的人工推导
III. 球窝关节的约束
- 1. 球窝关节约束的原理
- 2. 球窝关节约束的人工解读
- 3. 球窝关节约束梯度的符号计算
IV. 算法实现
V. 小结

本篇博客中, 如在引用段落中的是 AI 生成的内容. 此处主要用的是豆包. 因提示 “服务器繁忙，请稍后再试”, 没有用 Deepseek.

在正常段落中的是由博主真人输出的.

I. 论文回顾

论文 Joint axis and position estimation from inertial measurement data by exploiting kinematic constraints 由 Thomas Seel 等人撰写。文章提出利用关节运动学约束从惯性测量数据中估计关节轴和关节位置的新方法，经仿真和实验验证有效，可应用于机器人、车辆等领域, 尤其是外骨骼控制、人体运动跟踪等场景。

研究背景：惯性测量单元（IMU）在人体运动分析等领域应用广泛，但使用中存在两个问题：传感器偏差导致位置和角度估计漂移；需知道传感器坐标系相对关节轴或安装段的方向信息。现有解决方法存在局限性，因此需要能准确估计关节位置和轴的方法。

利用运动学约束

铰链关节约束：两个通过铰链关节连接的刚性段，其陀螺仪测量的角速度在关节平面投影长度相等，利用该特性可在传感器方向未知时识别铰链关节轴。通过计算相关梯度，使用高斯 - 牛顿算法可搜索满足条件的关节轴向量。此外，还需判断估计的关节轴向量是否对齐。
球窝关节约束：对于球窝关节，结合加速度计读数，可利用关节中心加速度相等的约束来估计关节中心到传感器坐标系原点的偏移向量，同样通过计算梯度并使用高斯 - 牛顿算法进行估计。

建模与仿真：开发三连杆运动学仿真模型，模拟传感器测量。对铰链关节轴和球窝关节偏移向量估计算法进行实现，采用特定参数化和更新过程。仿真结果表明，算法在不同运动、采样率和噪声幅度下表现良好，估计值能快速收敛到真实值附近。

实验结果：将算法应用于基于 IMU 的步态分析实验数据，实验中使用无线运动追踪器，让受试者进行腿部和脚部环绕运动及行走，记录传感器数据。结果显示，算法能在不到二十次迭代中正确识别膝关节轴和踝关节位置，虽存在一定误差，但最小二乘法能有效处理这些不准确性。

结论与展望：提出的最小二乘法能有效估计关节轴和位置，无需传感器安装知识和积分运算，对采样率要求低。该算法可应用于机器人操纵器、链接车辆等领域，未来将关注角度相关关节轴和位置的识别等扩展研究。

II. 铰接关节的约束

1. 铰接关节约束的原理

$\left\| g_{1}(t) × j_{1}\right\| _{2}-\left\| g_{2}(t) × j_{2}\right\| _{2}=0 \tag{1}$

两个通过铰链关节连接的刚性段，其陀螺仪测量的角速度在关节平面投影长度相等，利用该特性可在传感器方向未知时识别铰链关节轴，其原理涉及几何关系和运动学知识：

铰链关节的运动特性：铰链关节只允许两个刚性段在一个特定平面内相对转动，这个平面就是关节平面，而关节轴垂直于该平面。
两个刚性段虽可在空间自由旋转和移动，但相对运动受限于这个铰链关节的约束。
角速度的几何关系：分别安装在两个刚性段上的陀螺仪，测量得到各自的角速度 $g_{1}(t)$ 和 $g_{2}(t)$ 。
从几何角度看， $g_{1}(t)$ 和 $g_{2}(t)$ 的差异仅在于关节角的变化速度以及随时间变化的旋转矩阵。
因为它们围绕同一个铰链关节轴运动，所以在垂直于关节轴的平面（即关节平面）上的投影具有特殊性质。
投影长度相等的证明：设单位关节轴向量在第一段陀螺仪坐标系中为 $j_{1}$ ，在第二段陀螺仪坐标系中为 $j_{2}$ 。
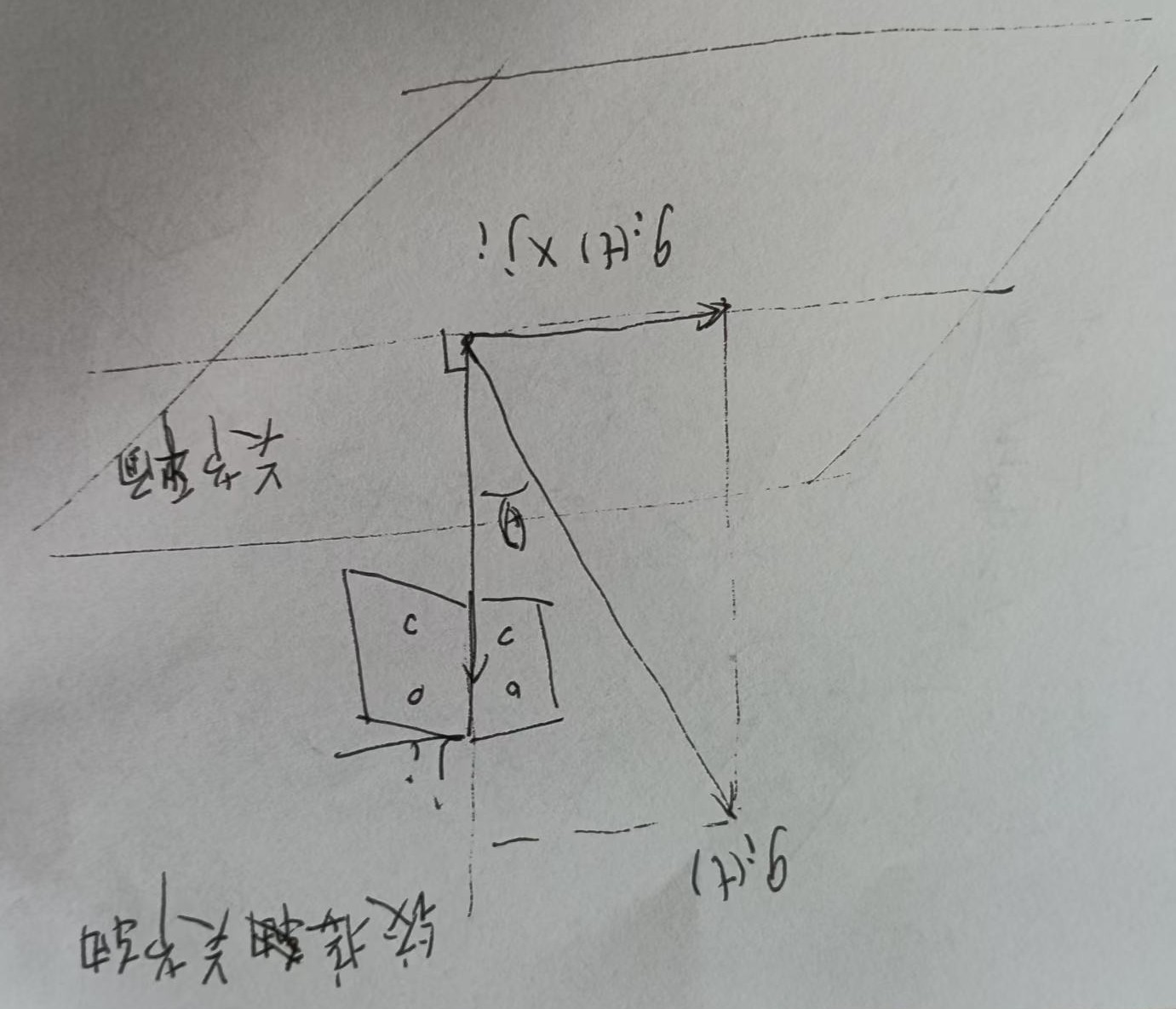
根据向量叉乘的几何意义，向量 $g_{i}(t)$ 与 $j_{i}$ 叉乘的结果，其模长 $\left\| g_{i}(t) × j_{i}\right\| _{2}$ 表示 $g_{i}(t)$ 在垂直于 $j_{i}$ 方向（即关节平面）上的投影长度。
由于两个刚性段围绕同一关节轴运动，在任意时刻 $t$ ， $g_{1}(t)$ 和 $g_{2}(t)$ 在关节平面的投影长度必然相等，即 $\left\| g_{1}(t) × j_{1}\right\| _{2}-\left\| g_{2}(t) × j_{2}\right\| _{2}=0$ 。
识别关节轴的方法：当传感器方向未知时，在大量的陀螺仪测量数据中，搜索满足 $\left\| g_{1}(t) × j_{1}\right\| _{2}-\left\| g_{2}(t) × j_{2}\right\| _{2}=0$ 的向量 $\hat{j_{1}}$ 和 $\hat{j_{2}}$ ，就能找到可能的关节轴方向。
通过计算相关梯度（如 $\frac{d\left(\left\| g_{i}(t) × j_{i}\right\| _{2}\right)}{d j_{i}}=\frac{\left(g_{i}(t) × j_{i}\right) × g_{i}(t)}{\left\| g_{i}(t) × j_{i}\right\| _{2}}$ ， $i = 1, 2$ ），并利用高斯-牛顿算法等优化方法，可在最小二乘意义下找到最符合条件的 $\hat{j_{1}}$ 和 $\hat{j_{2}}$ ，从而实现对铰链关节轴的识别。

在推导方程 (1) 时，向量 $g_{i}(t)$ 与 $j_{i}$ 叉乘的模长公式是基于向量叉乘的几何意义和性质得到的。

向量叉乘的几何意义：向量 $\vec{a}$ 与 $\vec{b}$ 叉乘 $\vec{a}\times\vec{b}$ ，其结果是一个向量，该向量的模长 $\vert\vec{a}\times\vec{b}\vert$ 等于 $\vert\vec{a}\vert\vert\vec{b}\vert\sin\theta$ ，其中 $\theta$ 是 $\vec{a}$ 与 $\vec{b}$ 之间的夹角。
在当前问题中，对于向量 $g_{i}(t)$ 与单位关节轴向量 $j_{i}$ （ $\vert j_{i}\vert = 1$ ），它们叉乘的模长 $\left\| g_{i}(t) × j_{i}\right\| _{2}$ ，根据上述几何意义，就等于 $\vert g_{i}(t)\vert\vert j_{i}\vert\sin\theta = \vert g_{i}(t)\vert\sin\theta$ ，这里 $\theta$ 是 $g_{i}(t)$ 与 $j_{i}$ 的夹角。
投影长度的表示：由于 $j_{i}$ 垂直于关节平面， $g_{i}(t)$ 与 $j_{i}$ 叉乘的模长 $\left\| g_{i}(t) × j_{i}\right\| _{2}$ ，实际上就是 $g_{i}(t)$ 在垂直于 $j_{i}$ 方向（即关节平面）上的投影长度。
从几何直观上理解，在以 $j_{i}$ 为法向量的关节平面上， $g_{i}(t)$ 在该平面的投影长度可以通过上述叉乘模长公式来表示，这是由向量运算的几何性质所决定的。

图形表示:

2. 铰接关节约束的梯度

以下是对梯度公式 $\frac{d\left(\left\| g_{i}(t) × j_{i}\right\| _{2}\right)}{d j_{i}}=\frac{\left(g_{i}(t) × j_{i}\right) × g_{i}(t)}{\left\| g_{i}(t) × j_{i}\right\| _{2}}$ 的推导过程：

明确符号与基本定义：
设 $g_{i}(t)$ 和 $j_{i}$ 为三维向量， $\times$ 表示向量的叉乘运算， $\left\| \cdot \right\| _{2}$ 表示向量的2 - 范数（即欧几里得范数）。对于向量 $\vec{a}=(a_1,a_2,a_3)$ ，其 2 - 范数 $\left\|\vec{a}\right\| _{2}=\sqrt{a_1^2 + a_2^2 + a_3^2}$ 。

对向量叉乘的模长函数求导：
令 $h(j_{i})=\left\| g_{i}(t) × j_{i}\right\| _{2}$ ，我们要计算 $\frac{dh(j_{i})}{d j_{i}}$ 。
根据向量叉乘的定义，若 $g_{i}(t)=(g_{i1}(t),g_{i2}(t),g_{i3}(t))$ ， $j_{i}=(j_{i1},j_{i2},j_{i3})$ ，则 $g_{i}(t) × j_{i}=(g_{i2}(t)j_{i3}-g_{i3}(t)j_{i2},g_{i3}(t)j_{i1}-g_{i1}(t)j_{i3},g_{i1}(t)j_{i2}-g_{i2}(t)j_{i1})$ 。
设 $u = g_{i}(t) × j_{i}$ ，那么 $h(j_{i})=\left\|u\right\| _{2}=\sqrt{u_1^2 + u_2^2 + u_3^2}$ 。
根据复合函数求导法则，我们先对 $h(j_{i})$ 关于 $u$ 求导，再乘以 $u$ 关于 $j_{i}$ 的导数。

对 $h(j_{i})=\sqrt{u_1^2 + u_2^2 + u_3^2}$ 关于 $u$ 求导：
根据求导公式 $(\sqrt{x})^\prime=\frac{1}{2\sqrt{x}}$ ，对 $h(j_{i})$ 关于 $u_k$ （ $k = 1, 2, 3$ ）求偏导数可得：
$\frac{\partial h(j_{i})}{\partial u_k}=\frac{u_k}{\left\|u\right\| _{2}}$ ，所以 $\frac{\partial h(j_{i})}{\partial u}=\frac{u}{\left\|u\right\| _{2}}$ （这里 $u$ 是向量形式）。
对 $u = g_{i}(t) × j_{i}$ 关于 $j_{i}$ 求导：
我们知道 $u_k$ 是关于 $j_{i1},j_{i2},j_{i3}$ 的线性函数。以 $u_1 = g_{i2}(t)j_{i3}-g_{i3}(t)j_{i2}$ 为例，对 $u_1$ 关于 $j_{i1}$ 求偏导数为 $0$ ，对 $u_1$ 关于 $j_{i2}$ 求偏导数为 $g_{i3}(t)$ ，对 $u_1$ 关于 $j_{i3}$ 求偏导数为 $g_{i2}(t)$ 。
同理可得 $u_2$ 和 $u_3$ 关于 $j_{i1},j_{i2},j_{i3}$ 的偏导数。
经过整理可以发现， $\frac{\partial u}{\partial j_{i}}=g_{i}(t)\times$ （这里“ $\times$ ”表示一种与叉乘相关的矩阵 - 向量运算结构，从结果上看等同于 $g_{i}(t)$ 再次与 $u$ 叉乘）。

应用链式法则：
根据链式法则 $\frac{dh(j_{i})}{d j_{i}}=\frac{\partial h(j_{i})}{\partial u}\cdot\frac{\partial u}{\partial j_{i}}$ ，将前面求得的结果代入：
$\frac{d\left(\left\| g_{i}(t) × j_{i}\right\| _{2}\right)}{d j_{i}}=\frac{u}{\left\|u\right\| _{2}}\cdot(g_{i}(t)\times)=\frac{\left(g_{i}(t) × j_{i}\right) × g_{i}(t)}{\left\| g_{i}(t) × j_{i}\right\| _{2}}$ 。

综上，得到了给定的梯度计算公式。

3. 铰接关节约束梯度的人工推导

曾经人工推导过如下. (AI 时代, 人工涂鸦看起来可能更温暖一点, 我们何去何从？)

III. 球窝关节的约束

1. 球窝关节约束的原理

场景与前提：
考虑由球窝关节连接的两个连杆，如原文中图 2 所示。球窝关节具有三个自由度，这意味着两个相连刚体可在多个方向上相对转动。由于这种多自由度的特性，两个传感器测量到的角速度之间不存在普遍的固定关系。为了利用运动学约束进行相关研究，需要引入加速度计的读数。

变量定义：
设两个传感器（分别位于两个连杆上）的加速度分别为 $a_{1}(t)$ 和 $a_{2}(t)$ ， $o_{1}$ 和 $o_{2}$ 分别是从关节中心到第一和第二传感器坐标系原点的偏移向量。
定义 $\Gamma_{g_{i}}(o_{i})$ ： $\Gamma_{g_{i}}(o_{i}) = g_{i}(t)\times(g_{i}(t)\times o_{i})+\dot{g}_{i}(t)\times o_{i}$ ， $i = 1, 2$ 。
$\Gamma_{g_{i}}(o_{i})$ 表示由于绕关节中心旋转而产生的（径向和切向）加速度。
它综合考虑了角速度 $g_{i}(t)$ 及其变化率 $\dot{g}_{i}(t)$ 与偏移向量 $o_{i}$ 的关系。
通过向量叉乘运算，体现了旋转运动对加速度的贡献。

方程（3）解释：
方程 $\left\| a_{1}(t)-\Gamma_{g_{1}}(o_{1})\right\| _{2}-\left\| a_{2}(t)-\Gamma_{g_{2}}(o_{2})\right\| _{2}=0 \ \forall t$ ，其含义是 $(a_{1}(t)-\Gamma_{g_{1}}(o_{1}))$ 表示在第一个局部坐标系下关节中心的加速度， $(a_{2}(t)-\Gamma_{g_{2}}(o_{2}))$ 表示在第二个局部坐标系下关节中心的加速度。
因为球窝关节连接的两个连杆在关节中心处的加速度，在不考虑坐标系旋转差异时应相等（这里忽略了旋转矩阵的影响，只考虑加速度的大小关系），所以两者加速度的欧几里得范数（即 $\left\| a_{1}(t)-\Gamma_{g_{1}}(o_{1})\right\| _{2}$ 和 $\left\| a_{2}(t)-\Gamma_{g_{2}}(o_{2})\right\| _{2}$ ）之差为0。
这个方程在任何时刻 $t$ 都成立，基于此，可以利用大量的数据集 $a_{1}(t_{k}), a_{2}(t_{k}), g_{1}(t_{k}), g_{2}(t_{k}))_{k = 1}^{N}$ 来估计 $o_{1}$ 和 $o_{2}$ 。

方程（4）解释：
方程 $\frac{d\left(\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}\right)}{d o_{i}}=\frac{\Gamma_{g_{i}}^{T}(a_{i}(t)-\Gamma_{g_{i}}(o_{i}))}{\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}}$ ， $i = 1, 2$ ，这是关于 $\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}$ 对 $o_{i}$ 的梯度公式。
其中 $\Gamma _{g_{i}}^{T}(o_{i})=(o_{i}\times g_{i}(t))\times g_{i}(t)+o_{i}\times \dot {g}_{i}(t)$ ，它是 $\Gamma_{g_{i}}$ 矩阵乘法表示形式的转置。
这个梯度公式在优化算法中非常重要，用于计算当 $o_{i}$ 发生微小变化时， $\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}$ 的变化率，进而通过迭代优化方法来求解 $o_{1}$ 和 $o_{2}$ ，以满足方程（3）的约束条件，实现从测量数据中准确估计关节中心到传感器坐标系原点的偏移向量。

2. 球窝关节约束的人工解读

绕关节中心旋转而产生的（径向和切向）加速度的人工推导：

关节中心加速度的人工推导如下.

说明：

为了推导方便，我们构建的全局坐标系. 而论文中都是基于瞬时固定的 IMU 局部坐标系来推导. 事实上, 瞬时固定的局部坐标系看作为了参考坐标系, 作用类似于全局坐标系. 瞬时固定的局部坐标系并不是固定在 IMU 上的随动局部坐标系, 而是 IMU 运动瞬时在外部惯性空间中与 IMU 随动坐标系瞬时重合的外部参考坐标系.

基于瞬时固定的 IMU 局部坐标系与我们引入的全局坐标系相差一个旋转矩阵. 相应得到的速度和加速度关系也相差一个旋转矩阵.

3. 球窝关节约束梯度的符号计算

$\frac{d\left(\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}\right)}{d o_{i}}=\frac{\Gamma_{g_{i}}^{T}(a_{i}(t)-\Gamma_{g_{i}}(o_{i}))}{\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}} \tag{4}$

简写 $\Delta_i \triangleq a_{i}(t)-\Gamma_{g_{i}}(o_{i})$ . 因为 $\Vert \Delta_i \Vert_2 = \sqrt{\Delta_i\cdot \Delta_i}$ , 可知式 (4) 左手边为
$\frac{d (\Vert \Delta_i \Vert_2 )}{d o_i} = \frac{d \sqrt{\Delta_i \cdot \Delta_i}}{d o_i} = \frac{1}{2\sqrt{\Delta_i \cdot \Delta_i}} \frac{d(\Delta_i \cdot \Delta_i)}{d o_i} = \frac{1}{2\Vert{\Delta_i }\Vert_2} \frac{d(\Delta_i \cdot \Delta_i)}{d o_i} \tag{4-a}$
式 (4) 右手边可以简写为
$\frac{\Gamma_{g_{i}}^{T}(a_{i}(t)-\Gamma_{g_{i}}(o_{i}))}{\left\| a_{i}(t)-\Gamma_{g_{i}}(o_{i})\right\| _{2}} = \frac{\Gamma_{g_{i}}^{T}(\Delta_i)}{\left\| \Delta_i \right\| _{2}} \tag{4-b}$
所以要证明式 (4) 成立, 只要验证
$\frac{1}{2} \frac{d(\Delta_i \cdot \Delta_i)}{d o_i} = {\Gamma_{g_{i}}^{T}(\Delta_i)} \tag{4-c}$
成立即可.

下面的推导计算比较复杂, 我们借用 Maxima 符号计算来推导. (不过结果和论文中相差一个负号)

/*Thomas Seel, etc. Joint Axis and Position Estimation from Inertial Measurement Data by Exploiting Kinematic Constraints*/
/*B. Constraints induced by sphernoidal joints*/
/* Derivation of Equation (4)*/
/*a---acceleration of IMU*/
/*o---offset vestor from the joint center to the origin of the IMU frame*/
/*g---angular velocity of the gyroscope(IMU)*/
/*dg---dg(t)/dt*/
/*Γ---the (radial and tangential) acceleration due to rotation around the joint center(spheroidal joint)*/
/*Gnorm---function to be derivated at left hand of equation (4). Derivatives with respect to vectors*/
/*DGnormX---X-component of the left hand of equation (4). Derivatives with respect to vectors*/
/*DGnormY---Y-component of the left hand of equation (4)*/
/*DGnormZ---Z-component of the left hand of equation (4)*/a:[a_x,a_y,a_z];
o:[o_x,o_y,o_z];
g:[g_x,g_y,g_z];
dg:[dg_x,dg_y,dg_z];
load("vect");
express(g~o);
Γ:(g~(g~o)+dg~o);
Γ2:express(Γ);
Γ2a:(a-Γ2);Gnorm: Γ2a.Γ2a$
DGnormX: expand(diff(Gnorm,o_x)/2);
/*numerator of the right hand of equation (4)*/
TΓ:(Γ2a~g)~g+Γ2a~dg$
TΓ2:express(TΓ)$/*X-component of the numerator of the right hand of equation (4)*/
expand(TΓ2[1]);DGnormY:expand(diff(Gnorm,o_y)/2);
/*Y-component of the numerator of the right hand of equation (4)*/
expand(TΓ2[2]);DGnormZ:expand(diff(Gnorm,o_z)/2);
/*Z-component of the numerator of the right hand of equation (4)*/
expand(TΓ2[3]);

IV. 算法实现

初始化：
设定输入数据，即获取 $N$ 个数据集 $g_{1}(t_{k}), g_{2}(t_{k}))_{k = 1}^{N}$ ，其中 $\gg 4$ 。这些数据代表在不同时刻 $t_{k}$ 从两个传感器获取的与关节运动相关的信息。
初始化变量 $x$ ，在估计球窝关节偏移向量时， $x$ 为 $o_{1}$ 和 $o_{2}$ 的拼接。这里 $o_{1}$ 和 $o_{2}$ 分别是从关节中心到第一和第二传感器坐标系原点的偏移向量。
(铰接关节的 $x$ 由公式 (5) 第一式定义)

关节轴估计：
利用公式（5），基于当前的 $x$ 值计算关节轴估计值 $\hat{j_{1}}$ 和 $\hat{j_{2}}$ 。
公式（5）建立了 $x$ 与 $\hat{j_{1}}$ 、 $\hat{j_{2}}$ 之间的数学关系，通过将 $x$ 的各个分量代入公式（5），按照规定的数学运算顺序进行计算，得出 $\hat{j_{1}}$ 和 $\hat{j_{2}}$ 的值。
同时，为保证估计的合理性，将关节轴估计值限制为单位长度，使得估计问题转化为四维。

计算误差与梯度：
[球窝关节] 定义误差函数 $\triangleq \left\|a_{1}(t) - \Gamma_{g_{1}}(o_{1})\right\|_{2} - \left\|a_{2}(t) - \Gamma_{g_{2}}(o_{2})\right\|_{2}$ 。其中 $a_{1}(t)$ 和 $a_{2}(t)$ 分别是两个传感器在时刻 $t$ 的加速度测量值， $\Gamma_{g_{1}}(o_{1})$ 和 $\Gamma_{g_{2}}(o_{2})$ 是与关节旋转相关的加速度项，通过此误差函数衡量当前估计的偏移向量 $o_{1}$ 和 $o_{2}$ 的准确性。
[铰接关节] 定义误差函数 $\triangleq \left\|\hat{j_{1}} × g_{1}(t_{k})\right\|_{2}-\left\|\hat{j_{2}} × g_{2}(t_{k})\right\|_{2}$ ，即两个范数的差值。如果关节轴估计准确，那么对于每个时刻 $t_{k}$ ， $\left\|\hat{j_{1}} × g_{1}(t_{k})\right\|_{2}$ 和 $\left\|\hat{j_{2}} × g_{2}(t_{k})\right\|_{2}$ 的值应该接近，此时 $e (k)$ 接近零。通过分析误差向量 $e$ 的值，可以评估关节轴估计的准确性，并进一步用于优化估计过程，例如在迭代算法中，根据误差向量 $e$ 来调整 $\hat{j_{1}}$ 和 $\hat{j_{2}}$ 的值，使得误差逐渐减小，从而得到更准确的关节轴估计。
根据公式（4）计算误差 $e$ 关于 $x$ 的梯度 $\frac{d e}{d x}$ 。公式（4）给出了关于误差对 $x$ 的导数形式，在计算过程中，需根据 $x$ 的具体形式（即 $o_{1}$ 和 $o_{2}$ 的拼接）以及误差函数 $e$ 的表达式，按照公式（4）的规则进行详细的数学推导和计算，得到梯度值。

更新变量 $x$ ：
使用公式 $pinv(\frac{d e}{d x}) e$ 更新变量 $x$ 。这里 $pinv(\frac{d e}{d x})$ 表示梯度 $\frac{d e}{d x}$ 的伪逆，通过该公式，让 $x$ 沿着负梯度方向（乘以误差 $e$ ）进行更新，步长由伪逆矩阵 $pinv(\frac{d e}{d x})$ 决定，使得误差 $e$ 逐渐减小。

循环与终止条件：
重复步骤 2 至 4，直到满足特定的终止条件。终止条件可以设定为误差 $e$ 小于某个预设的阈值，表明算法已经收敛到一个足够准确的结果；或者达到一定的迭代次数，防止算法无限循环。

噪声处理：
在计算过程中，由于 $g_{1}(t)$ 和 $g_{2}(t)$ 的时间导数对计算结果至关重要，且数据可能存在噪声干扰，采用一种抗噪声的非因果低通滤波器与简单的差商近似相结合的方法。
非因果低通滤波器用于去除数据中的高频噪声，使数据更加平滑；简单的差商近似则用于从离散的测量数据中估计 $g_{1}(t)$ 和 $g_{2}(t)$ 的时间导数，从而保证在噪声环境下算法仍能准确运行。
通过以上算法实现步骤，能够有效地估计关节轴及球窝关节的偏移向量，为后续相关问题的解决提供可靠的数据支持。