1 二分查找算法

二分查找算法是一种常用的查找算法，也被称为折半查找算法。它适用于有序数组的查找，并通过将待查找区间不断缩小一半的方式来快速定位目标值。

算法思想如下：

1. 首先，确定待查找数组的起始位置（通常为数组的第一个元素）和结束位置（通常为数组的最后一个元素）。
2. 然后，计算待查找区间的中间位置，即将起始位置和结束位置相加除以2。
3. 比较中间位置的元素与目标值的大小关系：

• 如果中间位置的元素等于目标值，则查找成功，返回中间位置。
• 如果中间位置的元素大于目标值，则目标值可能在左半部分，将结束位置更新为中间位置的前一个位置。
• 如果中间位置的元素小于目标值，则目标值可能在右半部分，将起始位置更新为中间位置的后一个位置。

4. 重复步骤2和步骤3，直到找到目标值或者待查找区间为空（起始位置大于结束位置）为止。

二分查找算法的时间复杂度为 $O(\log n)$ ，其中 $n$ 为数组的大小。由于每次查找都将待查找区间缩小一半，因此它比线性查找算法更加高效。

2 二分查找细节

区间开闭问题

• 左闭右闭区间：注意初始化时，$right=len(nums)-1$，数组最后一个元素位置。
• 左闭右开区间：注意初始化时，$right=len(nums)$，数组最后一个元素的下一个位置。
• 一般情况，全部使用「左闭右闭区间」这种写法。

$mid$ 取值问题

常见的两种取值公式

mid = (left + right) // 2   # 使用较多
mid = (left + right + 1) // 2

• 当待查找区间中的元素个数为奇数个，使用这两种取值公式都能取到中间元素的下标位置。
• 当待查找区间中的元素个数为偶数个
  • mid = (left + right) // 2 能取到中间靠左边元素的下标位置。
  • mid = (left + right + 1) // 2 能取到中间靠右边元素的下标位置。

出界条件的判断

两种判断方式

left <= right
left < right

• left <= right，并且查找的元素不在有序数组中，则 while 语句的出界条件是 left > right，也就是 left == right + 1，写成区间形式就是 [$right+1$,$right$]，此时待查找区间为空，待查找区间中没有元素存在，此时终止循环时，可以直接返回 −1。
• left < right，并且查找的元素不在有序数组中，则 while 语句出界条件是 left == right，写成区间形式就是 [$right$,$right$]。此时区间不为空，待查找区间还有一个元素存在，我们并不能确定查找的元素不在这个区间中，此时终止循环时，如果直接返回 −1 就是错误的。

使用 left < right 的话，可以在出界之后增加一层判断，判断是否等于目标元素。

# ...while left < right:# ...return left if nums[left] == target else -1

此时，在跳出循环的时候，一定是 left == right，无需判断此时应该返回 left or right

搜索区间范围的选择

三种写法

left = mid + 1，right = mid - 1
left = mid + 1 ，right = mid
left = mid，right = mid - 1

具体哪一种写法和二分查找的两种思路有关。

• 思路 1：「直接法」—— 在循环体中找到元素后直接返回结果。
• 思路 2：「排除法」—— 在循环体中排除目标元素一定不存在区间。

3 二分查找两种思路

3.1 直接法

1. 设定左右边界为数组两端，即 $left=0，right=len(nums)-1$，代表待查找区间为 $[left,right]$（左闭右闭区间）。
2. 取两个节点中心位置 $mid$ ，先比较中心位置值 $nums[mid]$ 与目标值 $target$ 的大小。
   1. 如果 $target==nums[mid]$，则返回中心位置。
   2. 如果 $target>nums[mid]$ ，则将左节点设置为 $mid+1$，然后继续在右区间 $[mid+1,right]$ 搜索。
   3. 如果 $target<nums[mid]$，则将右节点设置为 $mid-1$，然后继续在左区间 $[left,mid-1]$ 搜索。
3. 如果左边界大于右边界，查找范围缩小为空，说明目标元素不存在，此时返回 −1。

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1# 在区间 [left, right] 内查找 targetwhile left <= right:# 取区间中间节点mid = left + (right - left) // 2# 如果找到目标值，则直接范围中心位置if nums[mid] == target:return mid# 如果 nums[mid] 小于目标值，则在 [mid + 1, right] 中继续搜索elif nums[mid] < target:left = mid + 1# 如果 nums[mid] 大于目标值，则在 [left, mid - 1] 中继续搜索else:right = mid - 1# 未搜索到元素，返回 -1return -1

3.2 排除法

1. 设定左右边界为数组两端，即 $left=0，right=len(nums)-1$，代表待查找区间为 $[left,right]$（左闭右闭区间）。
2. 取两个节点中心位置 $mid$ ，比较中心位置值 $nums[mid]$ 与目标值 $target$ 的大小，先将目标元素一定不存在的区间排除。
3. 然后在剩余区间继续查找元素，继续根据条件排除目标元素一定不存在的区间。
4. 直到区间中只剩下最后一个元素，然后再判断这个元素是否是目标元素。

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1# 在区间 [left, right] 内查找 targetwhile left < right:# 取区间中间节点mid = left + (right - left) // 2# nums[mid] 小于目标值，排除掉不可能区间 [left, mid]，在 [mid + 1, right] 中继续搜索if nums[mid] < target:left = mid + 1 # nums[mid] 大于等于目标值，目标元素可能在 [left, mid] 中，在 [left, mid] 中继续搜索else:right = mid# 判断区间剩余元素是否为目标元素，不是则返回 -1return left if nums[left] == target else -1

• 直接法：更适合解决简单题目，数组中是非重复元素。
• 排除法：更适合解决复杂题目，数组里可能不存在的元素，找边界问题。

task09

704. 二分查找

思路

• 上来就是一个二分查找
• 取中间值，然后根据中间值和目标值之间的大小确定比较的区间
• 如果不存在目标值就返回 -1

代码

class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1      # 设定左右边界while left <= right:mid = (left + right) // 2       # 取中间节点if nums[mid] == target:         # 中间节点值等于目标值，返回中间位置return midelif nums[mid] > target:        # 中间节点值大于目标值，区间换成[left, mid-1]right = mid - 1 else:left = mid + 1              # 中间节点值小于目标值，区间换成[mid+1, right]return -1

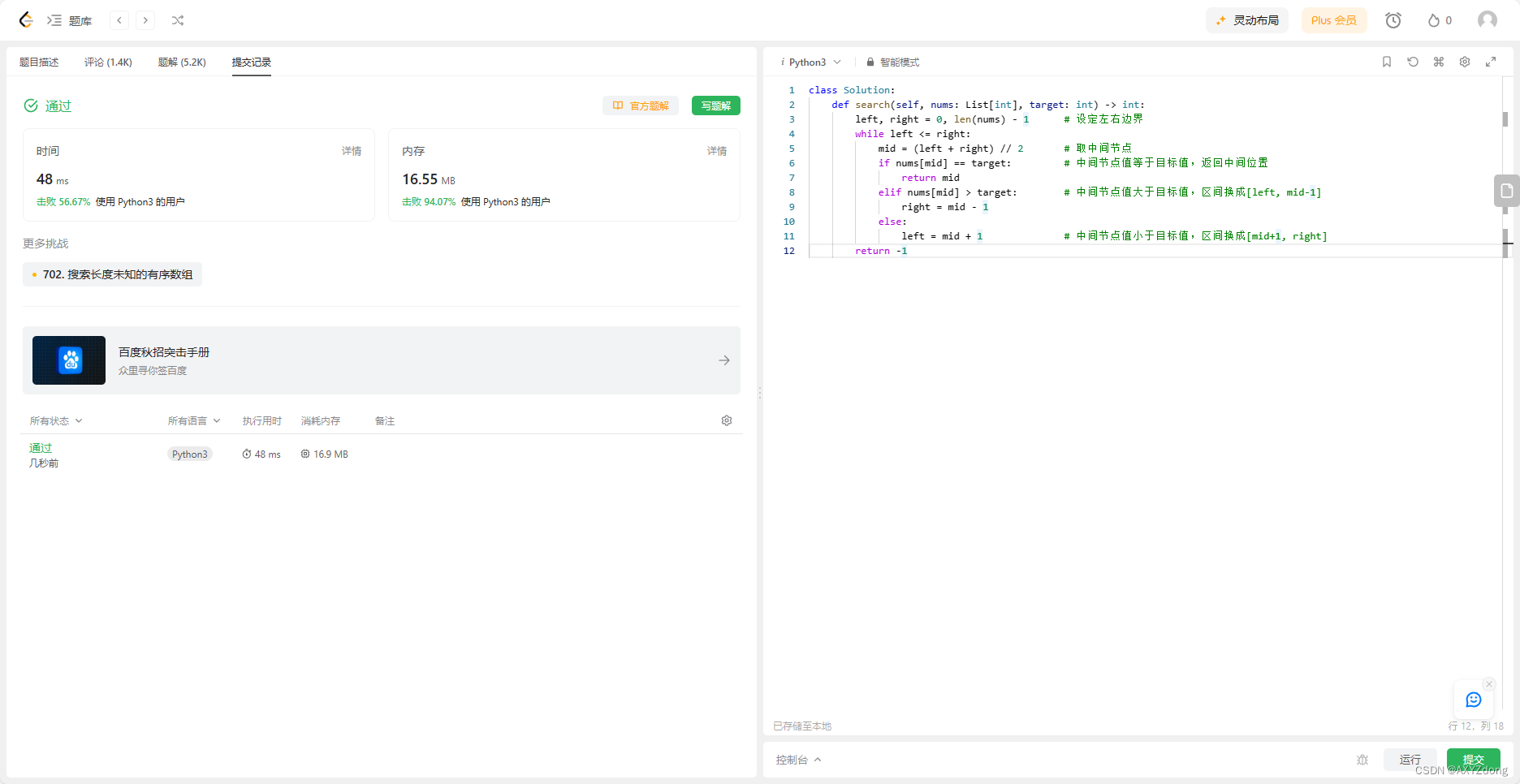
35. 搜索插入位置

思路

• 上手就是一个二分查找
• 对于目标值不存在的情况，直接返回左端下标值，即被顺序插入的位置

代码

class Solution:def searchInsert(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1while left <= right:mid = (left + right) // 2if nums[mid] == target:return midelif nums[mid] > target:right = mid - 1else:left = mid + 1return left                 # 目标值不存在，直接返回左端下标值

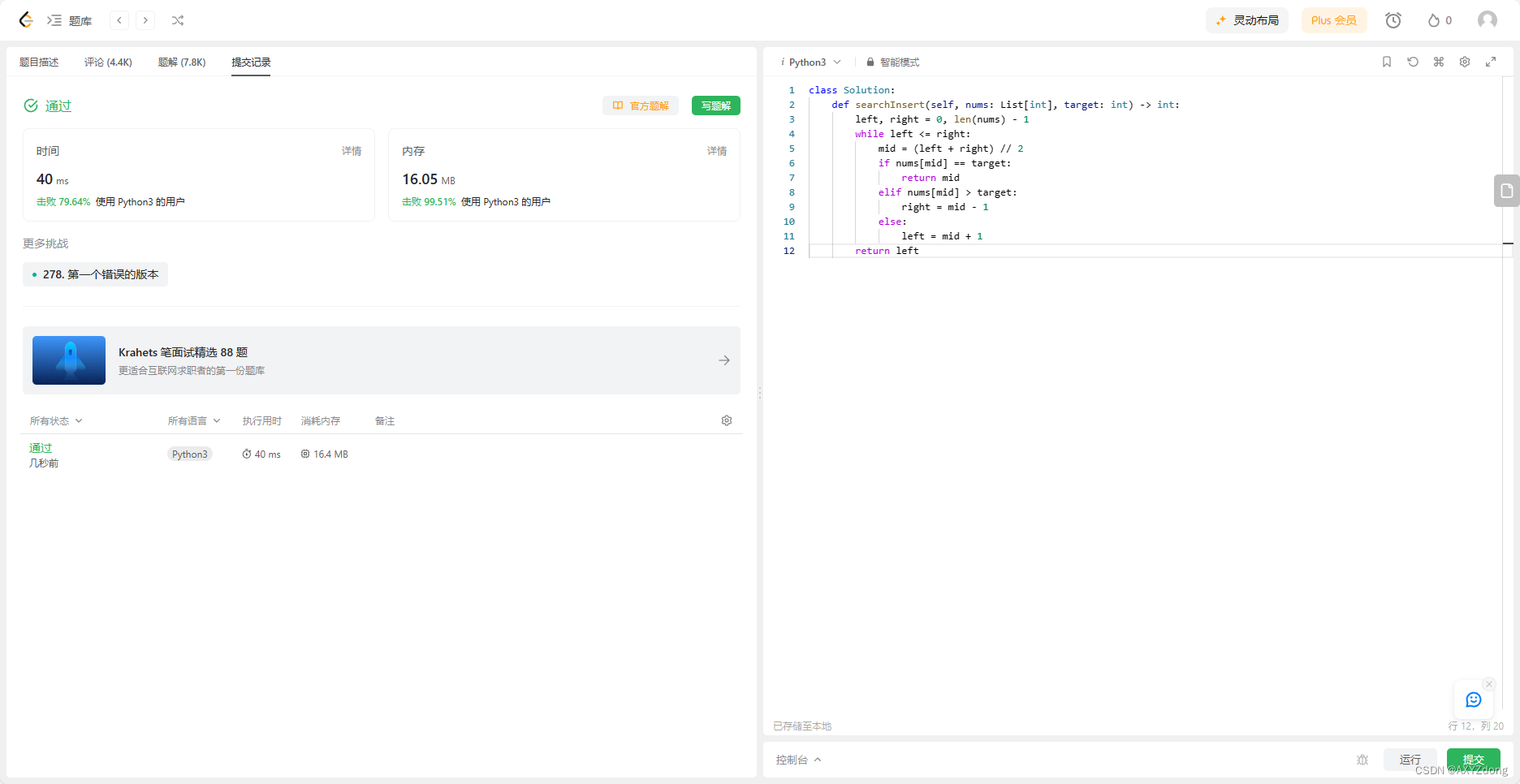
374. 猜数字大小

思路

• 本质上还是二分查找，只不过是使用预定义的接口比较大小

代码

# The guess API is already defined for you.
# @param num, your guess
# @return -1 if num is higher than the picked number
#          1 if num is lower than the picked number
#          otherwise return 0
# def guess(num: int) -> int:class Solution:def guessNumber(self, n: int) -> int:left, right = 1, nwhile left <= right:mid = (left + right) // 2result = guess(mid)if result == 0:return midelif result == -1:right = mid - 1else:left = mid + 1

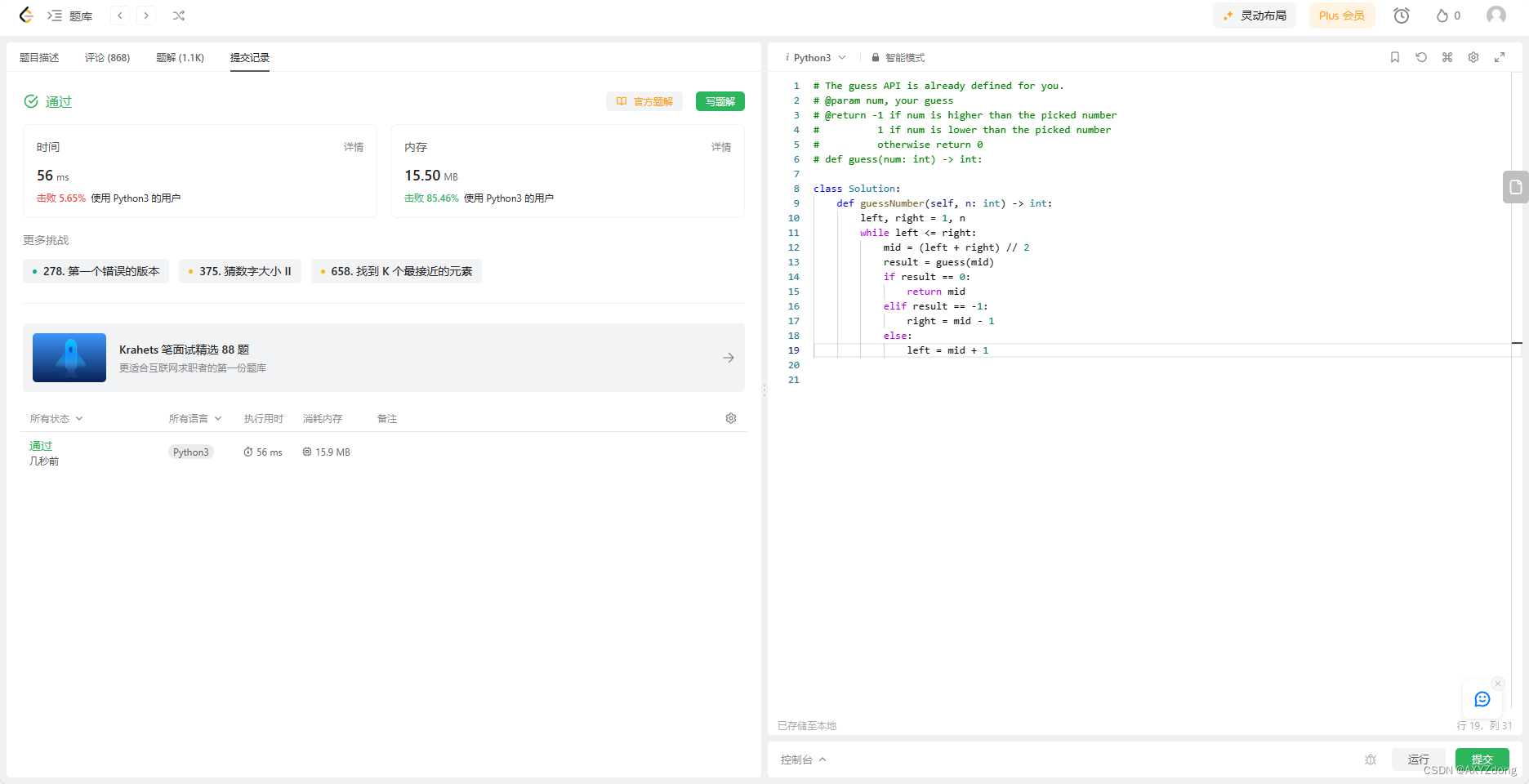
task10

69. x 的平方根

思路

• 本质上是二分查找，使用中间值的平方和目标值进行比较
• 小于等于目标值，缩小左端，继续进行二分，直到中间值的平方大于目标值，返回中间值作为结果
• 需要注意的是目标值是0和1的特殊情况

代码

class Solution:def mySqrt(self, x: int) -> int:left, right, res = 0, x, -1if x == 0 or x == 1:return xwhile left <= right:mid = (left + right) // 2if mid * mid <= x:res = midleft = mid + 1else:right = mid - 1return res

参考文献

• [1] https://datawhalechina.github.io/leetcode-notes/#/

—— END ——

---

如果以上内容有任何错误或者不准确的地方，欢迎在下面 👇 留言。或者你有更好的想法，欢迎一起交流学习~~~

更多精彩内容请前往 AXYZdong的博客