文章目录
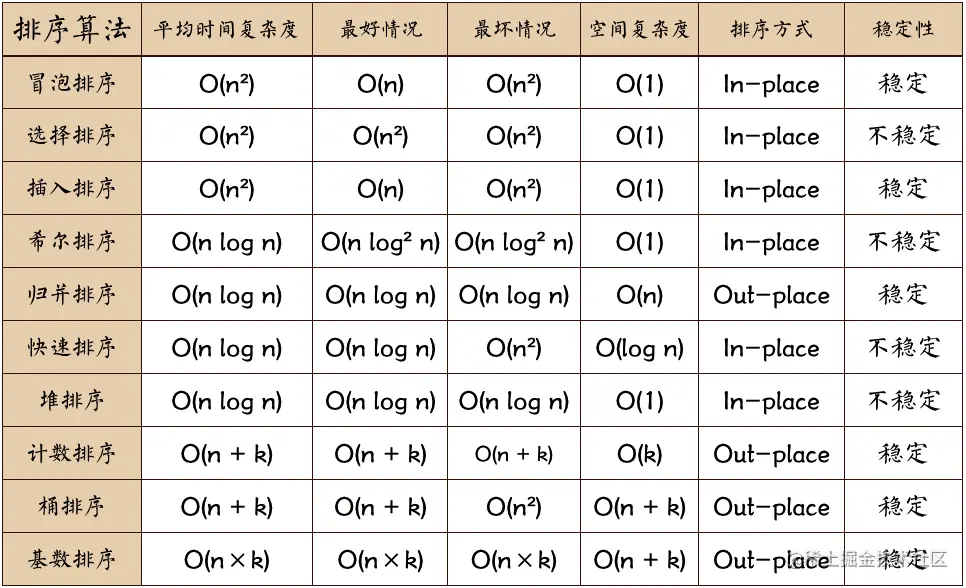
- 关于排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
关于排序算法
稳定排序: 在排序过程中具有相同键值的元素,在排序之后仍然保持相对的原始顺序。意思就是说,现在有两个元素a和b,a排在b的前面,且a==b,排序之后a仍然在b的前面,这就是稳定排序。
非稳定排序: 在排序过程中具有相同键值的元素,在排序之后可能会改变它们的相对顺序。意思是说,现在有两个元素a和b,在原始序列中a排在b前面,排序之后a可能会出现在b后面,它们的相对位置可能会发生变化。
原地排序: 在排序过程中不需要申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。这意味着在原地排序中,排序操作会直接修改原始数据,而不需要创建新的数据结构来存储排序后的结果。
非原地排序: 在排序过程中需要申请额外的存储空间来存储临时数据或排序结果,而不直接在原始数据上进行修改。
冒泡排序
基本思路: 通过相邻元素之间的比较和交换,将排序码小的元素逐渐从底部移向顶部。由于整个排序的过程就像水底下的气泡一样逐渐向上冒,因此称为冒泡排序。
操作步骤:
- 比较相邻的两个元素。如果第一个元素比第二个元素大,就交换这两个元素;
- 重复上述步骤,直到数组末尾;
- 重复上述两个步骤,直到完成排序。
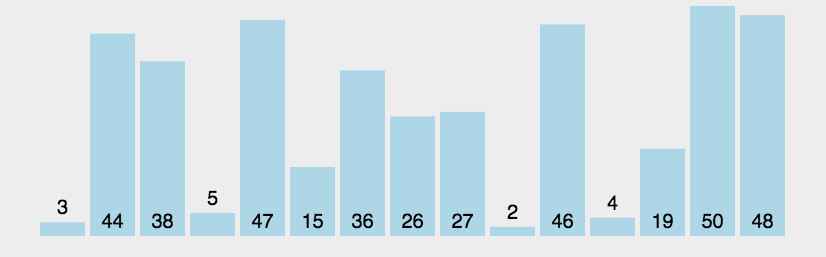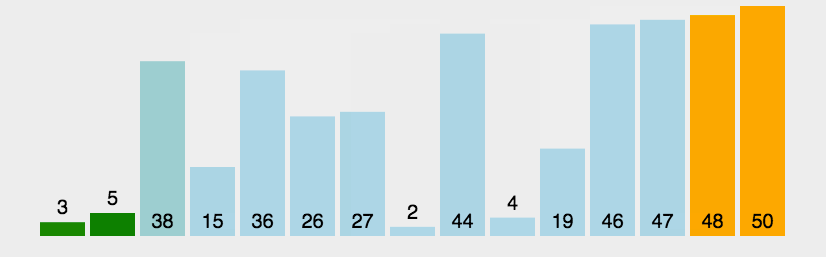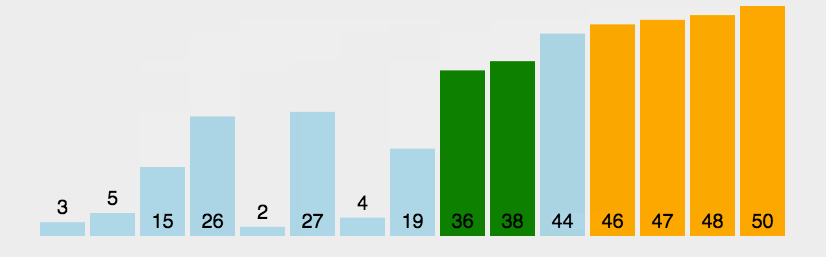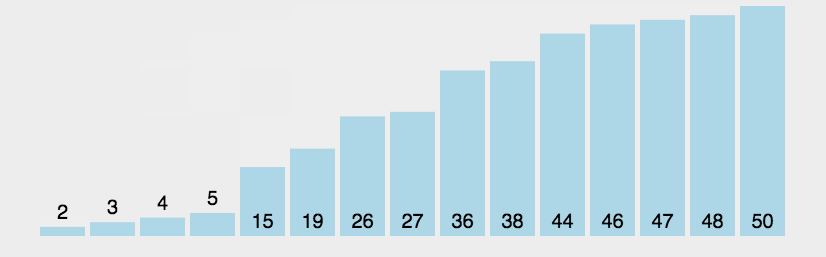
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function BubbleSort(arr) {for (let i in arr) {// 每次循环都能找到一个最大的数放在最右边for (let j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {let temp = arr[j]arr[j] = arr[j + 1]arr[j + 1] = temp}}}console.log(arr);return arr}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]BubbleSort(a)</script>
总结: 稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
选择排序
基本思路: 首先在未排序序列中找到最小(大)元素,存放到排序的起始位置,接着再从剩余末排序元素中继续寻找最小(大)元素,放到已排序序列的起始位置。以此类推,直到所有的元素均已排序完毕。
操作步骤:
- 在数列范围内找到最小(大)元素,与起始位置元素进行交换;
- 除已经排序过的元素外,在剩余数列范围内找到最小(大)元素,与剩余数列的起始位置元素进行交换。
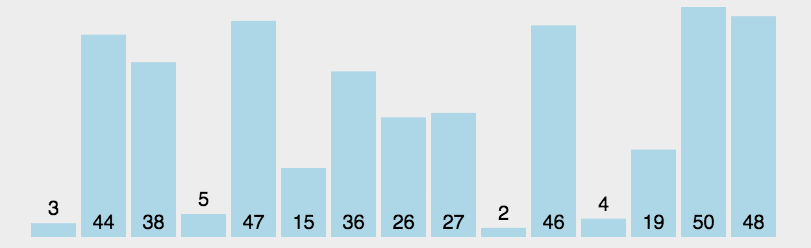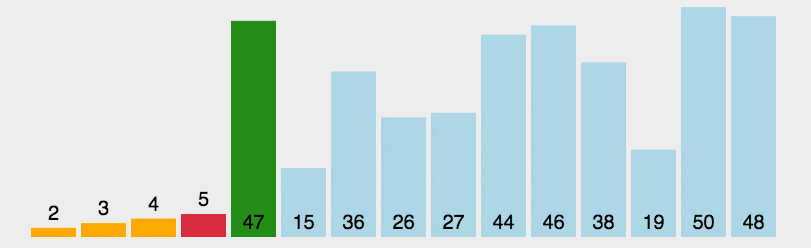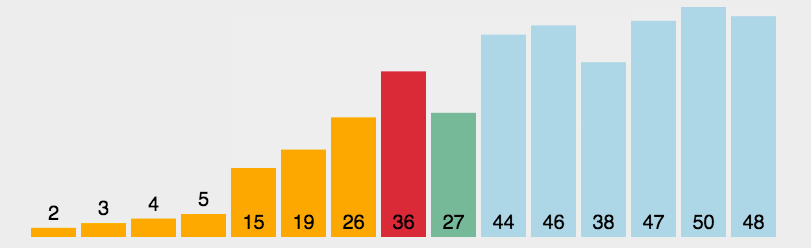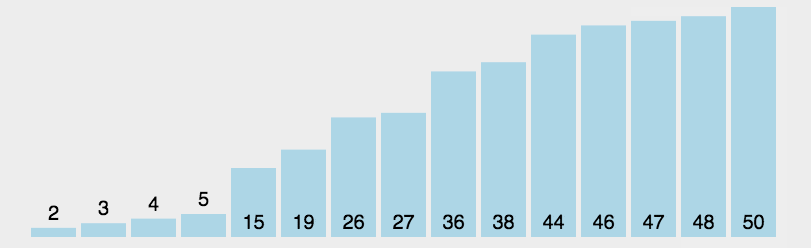
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function SelectionSort(arr) {for (let i in arr) {// 声明一个变量,用来接收当前最小值的下标let min = ifor (let j = i; j < arr.length; j++) {if (arr[j] < arr[min]) {min = j}}let temp = arr[i]arr[i] = arr[min]arr[min] = temp}console.log(arr);return arr}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]SelectionSort(a)</script>
分析: 不稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
插入排序
基本思路: 将数组分为两部分,一部分是已排序的,一部分是未排序的。初始时,已排序部分只包含数组的第一个元素,然后依次将未排序部分的元素插入已排序部分,使得已排序部分仍然保持有序。
操作步骤:
- 将第一个数作为基准,取出第二个数与其进行比较,如果比它大就放右边,比它小就放左边;
- 取出第三个数,与前一个数进行比较,比它大就放右边,比它小就再往前一个数进行比较,直到遇到一个比它小的数;
- 一直重复上述步骤
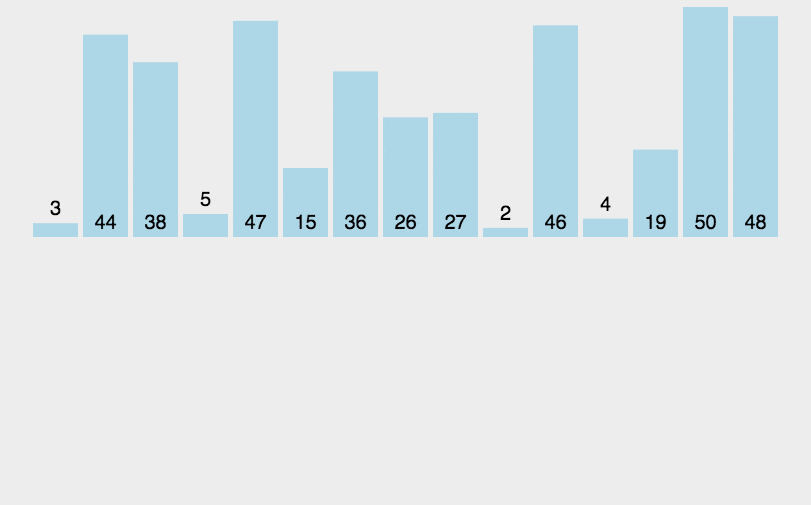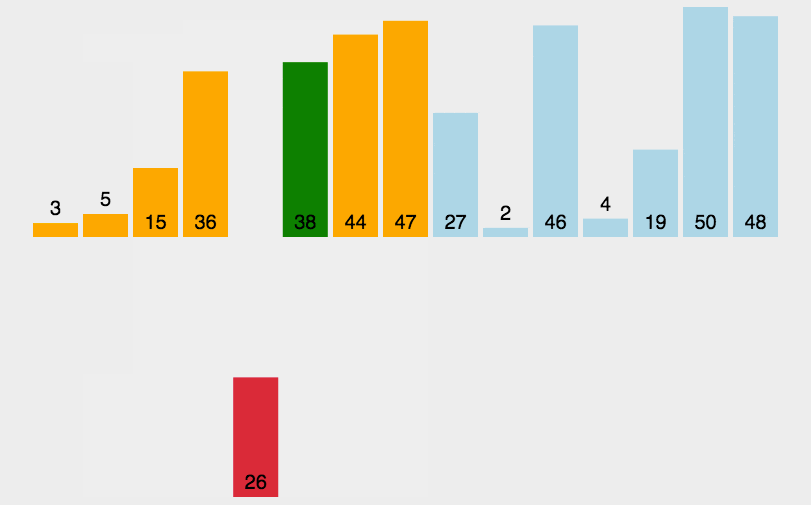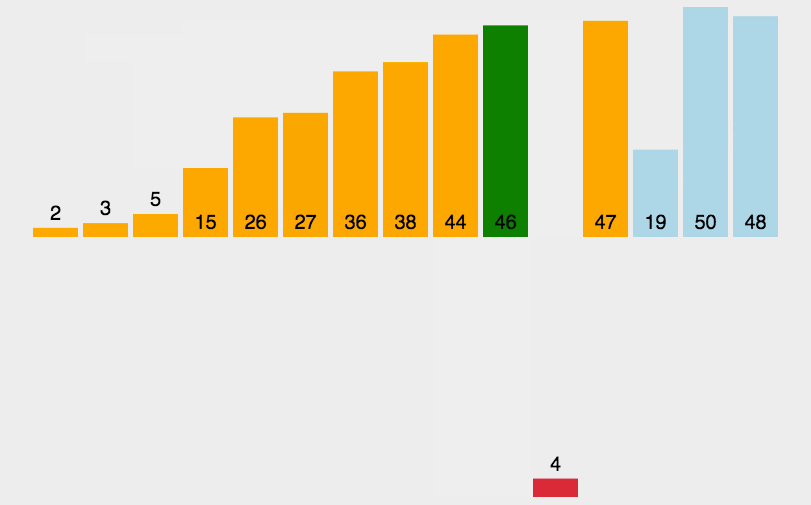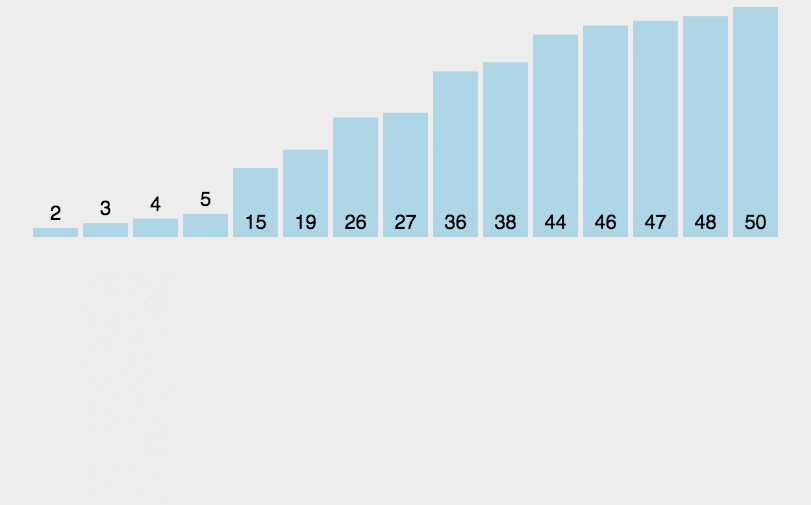
例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function InsertionSort(arr) {// 以第一个数作为基准for (let i = 1; i < arr.length; i++) {let temp = arr[i]let j;// 如果遍历的元素大于取出的元素,则遍历过的元素都需要后移一位for (j = i - 1; j >= 0 && a[j] > temp; j--) {arr[j + 1] = arr[j]}arr[j + 1] = temp}console.log(arr);}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]InsertionSort(a)</script>
分析: 稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(n²)。
希尔排序
基本思路: 它是插入排序的一种改进版本,通过将原始数组分成多个子序列,利用插入排序对子序列进行排序,最终合并成一个有序序列。
操作步骤:
- 选择一个增量序列(间隔序列),通常初始增量为数组长度的一半,然后逐渐减小增量;
- 按照增量将原始数组分成多个子序列。每个子序列可以视为一个小型数组;
- 对每个子序列应用插入排序算法,将子序列中的元素进行排序;
- 逐渐缩小增量,重复上述步骤,直到增量为 1;
- 最后一次增量为 1 时,整个数组被视为一个序列,再次应用插入排序。
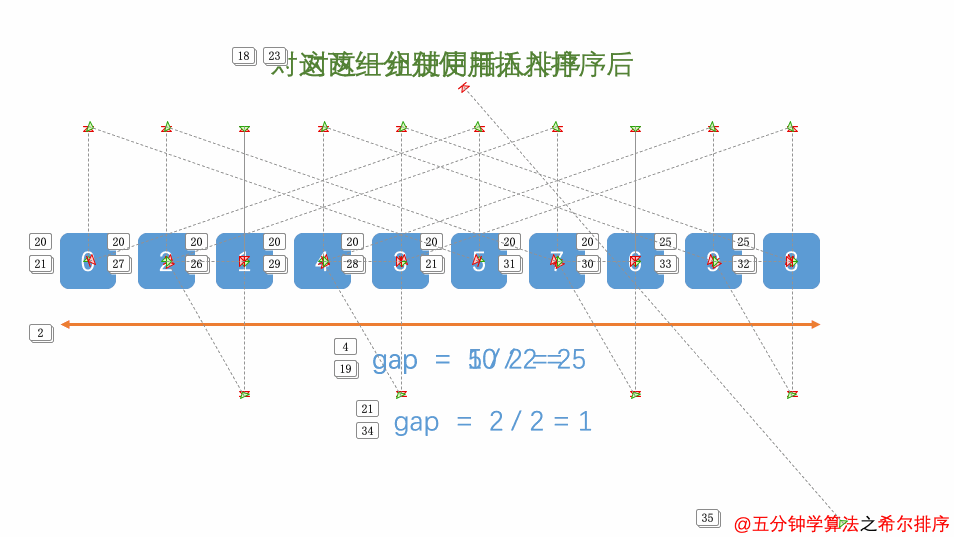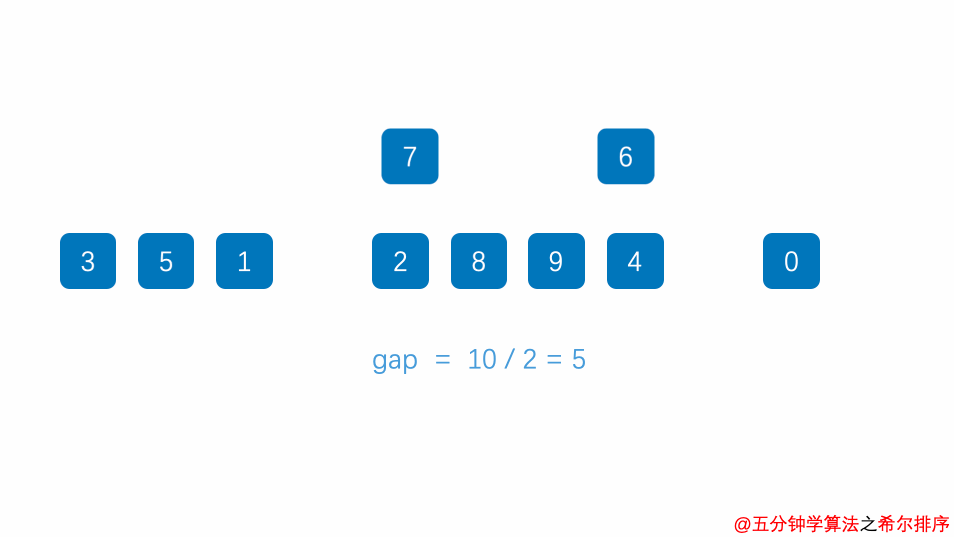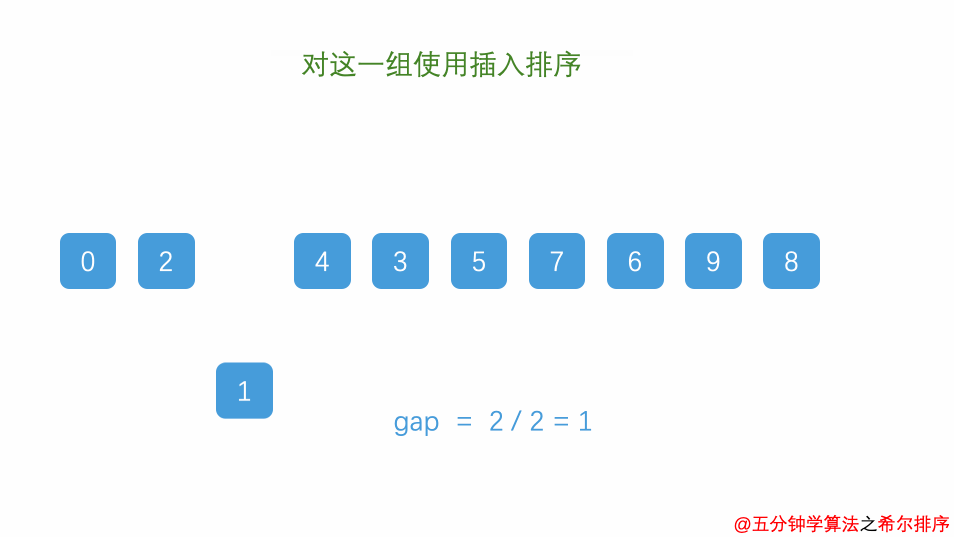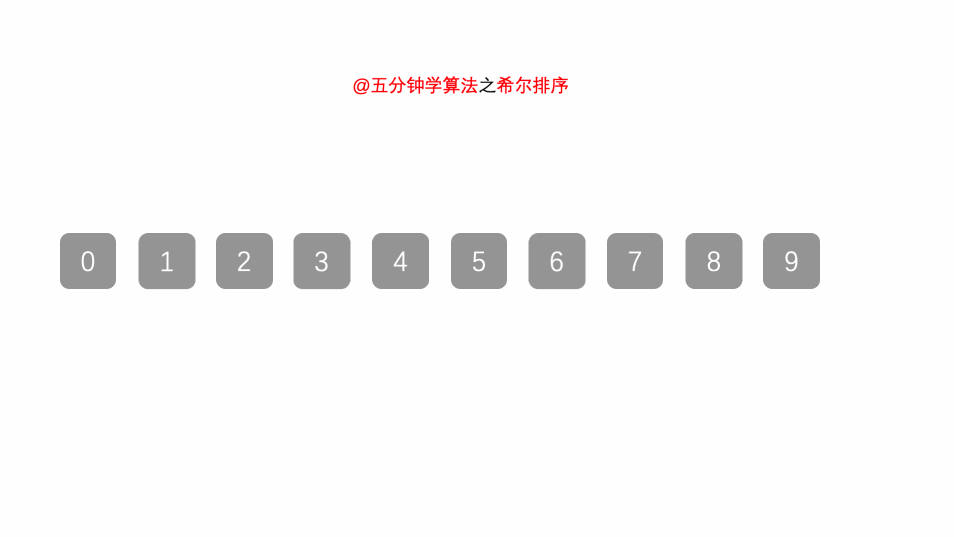
例题:
对
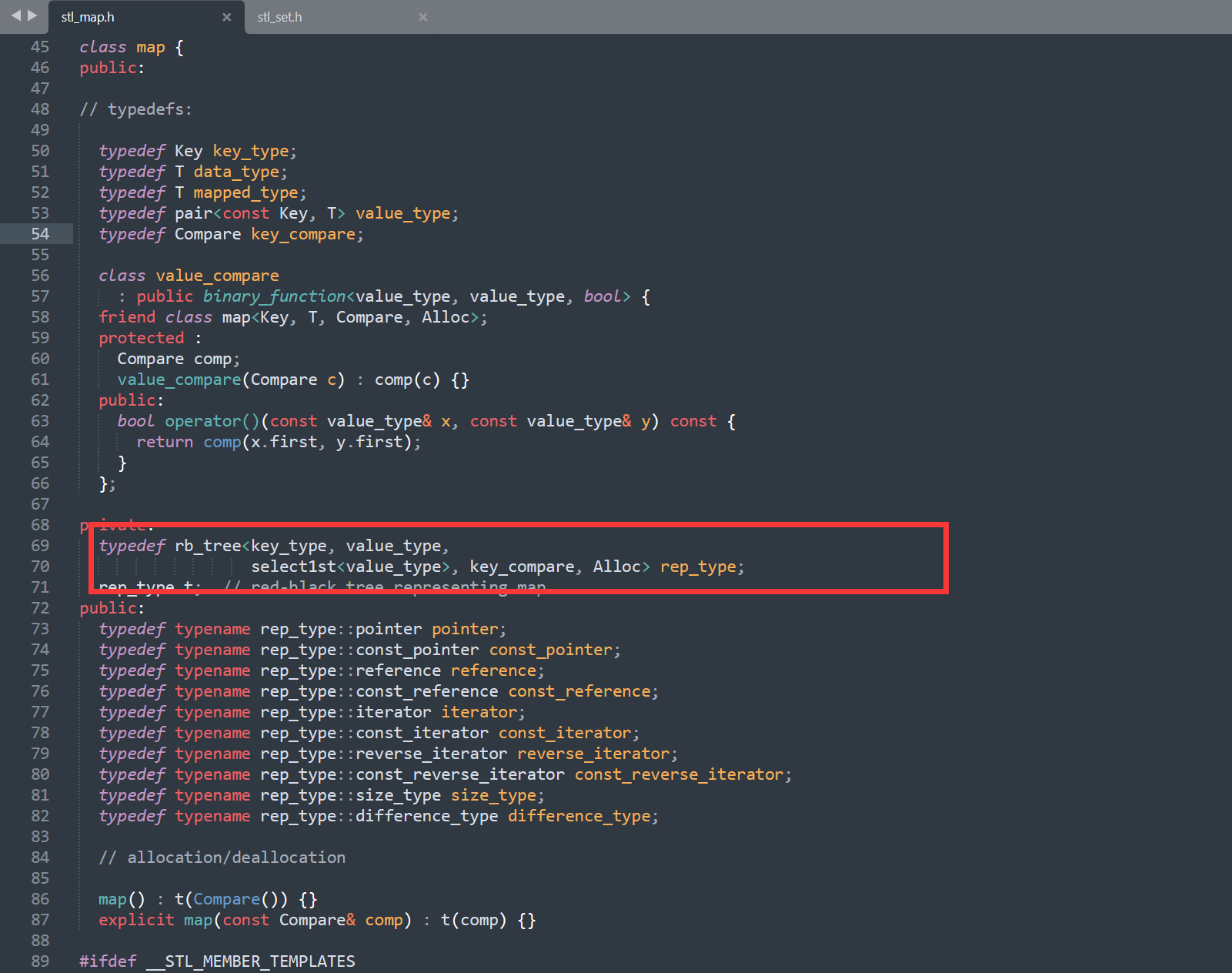
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function ShellSort(arr) {// 选择初始的增量(gap)为数组长度的一半Math.floor(arr.length / 2)for (let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap / 2)) {// 对每个子序列进行插入排序for (let i = gap; i < arr.length; i++) {const temp = arr[i]let j;for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j]}arr[j + gap] = temp}}console.log(arr);}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]ShellSort(a)</script>
分析: 不稳定排序,需要开辟极少的空间,空间复杂度为O(1),时间复杂度为O(nlog(n))。
归并排序
基本思路: 它是一种基于分治策略的排序算法,通过将待排序的数组分割成若干个子序列,分别排序后再合并这些子序列,以达到整体有序的目的。归并排序的主要步骤包括分割、排序和合并三个阶段。
操作步骤:
- 分割:将待排序的数组分成两个大致相等的子数组,递归地对这两个子数组进行排序;
- 排序:递归地对每个子数组进行排序,直到子数组的长度为1(只有一个元素),此时认为它是有序的;
- 合并:将排好序的子数组合并成一个新的有序数组,这一步的关键是将两个有序的子数组合并成一个更大的有序数组。

例题:
对
a=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]进行从小到大排序。
<script>function MergeSort(arr) {if (arr.length <= 1) return arr;// 分割数组const middle = Math.floor(arr.length / 2)const left = arr.slice(0, middle)const right = arr.slice(middle)// 递归分割+排序const leftSort = MergeSort(left)const rightSort = MergeSort(right)return SequencSort(leftSort, rightSort)}function SequencSort(left, right) {let result = []let leftIndex = 0;let rightIndex = 0;// 合并两个有序数组while (leftIndex < left.length && rightIndex < right.length) {if (left[leftIndex] < right[rightIndex]) {result.push(left[leftIndex])leftIndex++} else {result.push(right[rightIndex])rightIndex++}}// 将剩余的元素添加到结果中return result.concat(left.slice(leftIndex), right.slice(rightIndex))}let a = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]MergeSort(a)</script>
分析: 稳定排序,空间复杂度为O(n),时间复杂度为O(nlog(n))。