🌈write in front🌈
🧸大家好，我是Aileen🧸.希望你看完之后，能对你有所帮助，不足请指正！共同学习交流.
🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如需转载还请通知⚠️
📝个人主页：Aileen_0v0🧸—CSDN博客
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​
📣系列专栏：Aileen_0v0🧸的数据结构与算法学习系列专栏🌸——CSDN博客
🗼我的格言:"没有罗马,那就自己创造罗马💫~"

目录

​编辑

​编辑

回顾 🧸

​编辑

中缀表达式🀄

全括号表达式与前后缀表达式的关系🎡

中缀表达式转换为前后缀形式的方法🪐

通用的中缀转后缀算法⭐

利用中缀转后缀的操作流程🪂

转成后缀表达式对应的代码🚀

---

 

回顾 🧸

"温故而知新"

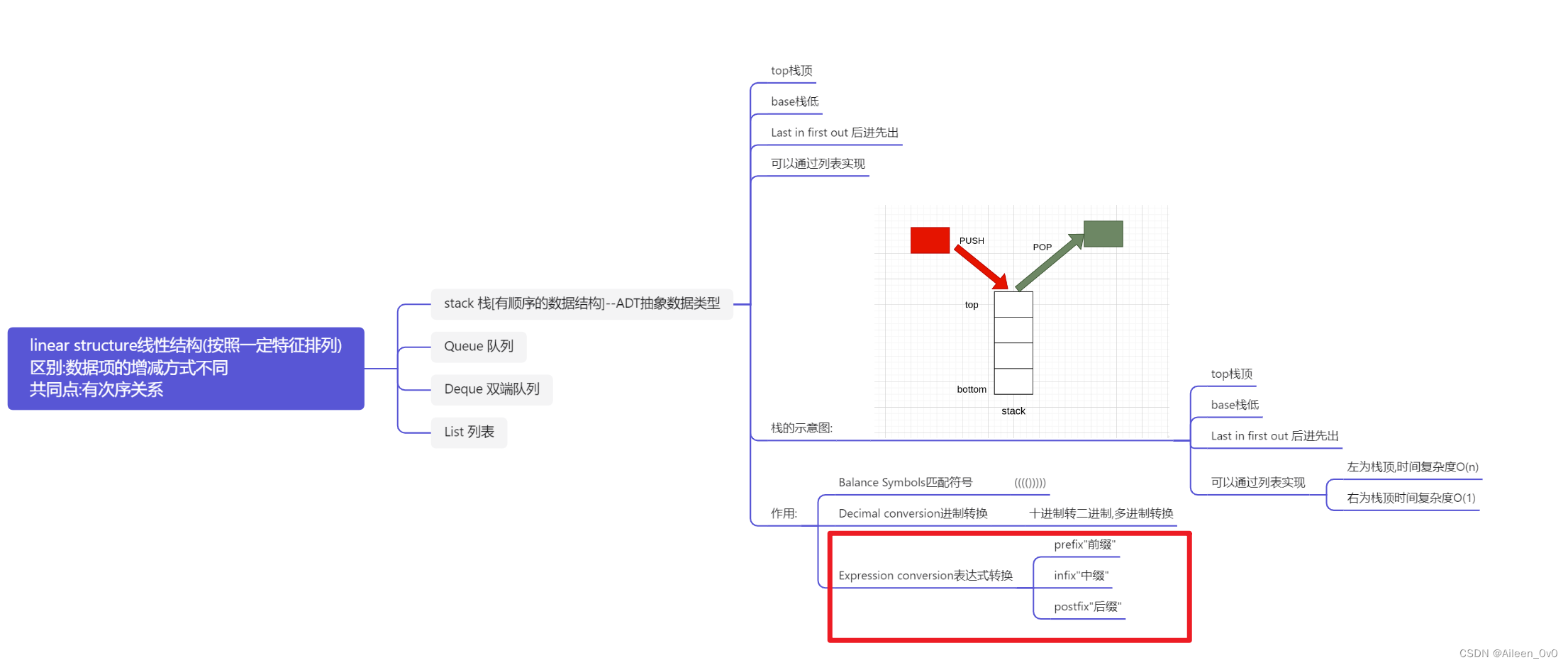
通过思维导图回顾一下我们学了什么,我们先学了什么是线性结构,栈(Stack)是一种抽象数据类型的线性结构,栈是什么,栈的特点以及操作步骤,我们还可以通过列表去实现栈,不过不同的栈顶其对应的时间复杂度也不同,了解完栈的基础知识点后我们开始学习栈的应用,栈可以用于

「(1)匹配符号(Balance Symbols),

    (2)进制转换(Decimal conversion),

    (3)表达式转换(Experssion conversion)」

(1) 和 (2) 我们已经在前面的文章写过了:不记得知识点或者对前面内容感兴趣的小伙伴可以点击👉

🔗(1)http://t.csdnimg.cn/Ypv3q

🔗(2)http://t.csdnimg.cn/OLIJW

对应专栏数据结构与算法学习系列专栏🌸🔗:http://t.csdnimg.cn/6BQDo

中缀表达式🀄

我们通常看到的表达式如:B*C , 很容易就知道是B乘以C

像  *  这种操作符( operator ) 介于操作数 ( operand )中间的表示法,称为 "中缀" 表示法.

But sometimes 中缀表示法会 case confusion(引起混淆),如 "A + B * C"

是A+B然后再乘以C  还是B*C然后再加A?

为了消除混淆,人们引入"优先级"的概念

规定高优先级的操作符先计算
相同优先级的操作符从左到右依次计算这样A+B*C就没有疑义是A加上 B与C的乘积
同时引入了括号来表示强制优先级，括号的优先级最高，而且在嵌套的括号中，内层的优先级更高这样(A+B)*C就是A与B的和再乘以C

---

全括号表达式与前后缀表达式的关系🎡

虽然人们已经习惯了这种表示法，但计算机处理最好是能明确规定所有的计算顺序，这样无需处理复杂的优先规则
于是,我们引入全括号表达式:

在所有的表达式项两边都加上括号A+B*C+D，应表示为((A+(B*C))+D)
可否将表达式中操作符的位置稍移动一下?

例如中缀表达式A+B将操作符移到前面，变为"+AB"
或者将操作符移到最后，变为“AB+”
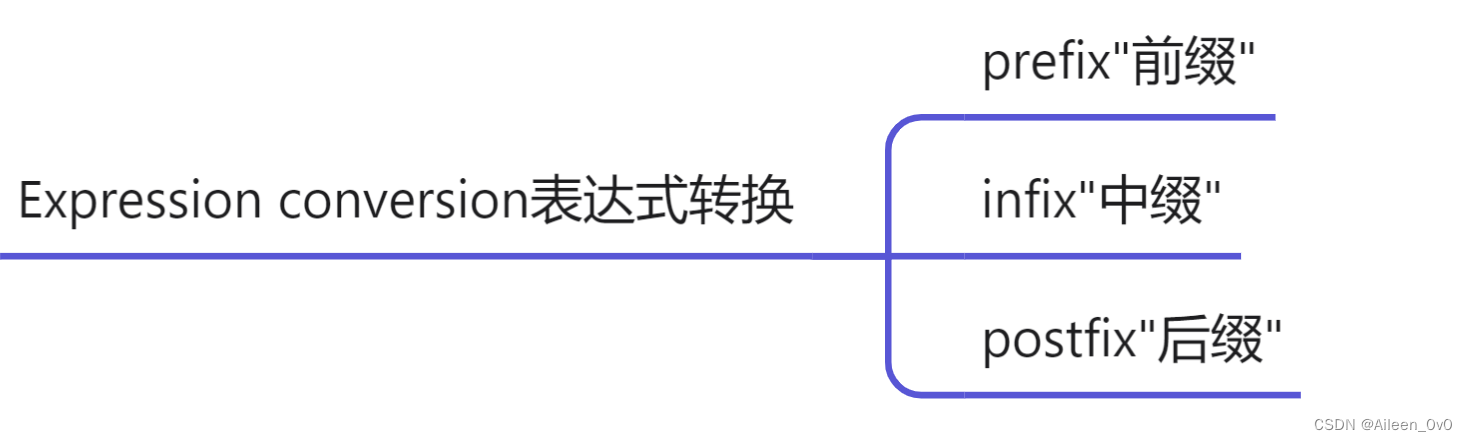
我们就得到了表达式的另外两种表示法:"前缀"和“后缀”表示法以操作符相对于操作数的位置来定义

这样A+B*C将变为前缀的"+A*BC"后缀的"ABC*+"为了帮助理解，子表达式加了下划线

在前缀和后缀表达式中,操作符的次序完全决定了运算的次序，不再有混淆

所以在很多情况下，表达式在计算机中的表示都避免使用复杂的中缀形式

让我们先看看这些前中缀和后缀表达式

中缀表达式	前缀表达式	后缀表达式
A + B * C + D	+ + A * B C D	A B C * + D +
( A + B ) * ( C + D )	* + A B + C D	A B + C D + *
A * B + C * D	+ * A B * C D	A B * C D * +
A + B + C + D	+ + + A B C D	A  B + C + D +

想必初看的小伙伴会觉得眼花缭乱,但是不要着急,我们接下来会一一讲解.

一定得有个算法来转换任意复杂的表达式

为了分解算法的复杂度，我们从“全括号中缀表达式入手我们看A+B*C，

如果写成全括号形式:(A+(B*C))，显式表达了计算次序我们注意到每一对括号，都包舍了一组完整的操作符和操作数,让我们看看如何将其转换成前后缀表达式吧~

---

中缀表达式转换为前后缀形式的方法🪐

✨Summary:

        (1)将中缀表达式转换为全括号形式

        (2)将所有的操作符移动到子表达式所在的 左括号(前缀prefix) 或者 右括号(后缀postfix) 处~

              替代之,再删除所有的括号.

---

通用的中缀转后缀算法⭐

在中缀表达式转换为后缀形式的处理过程中，操作符比操作数要晚输出

所以在扫描到对应的第二个操作数之前，需要把操作符先保存起来

而这些暂存的操作符，由于优先级的规则还有可能要反转次序输出.

在A+B*C中，+虽然先出现，但优先级比后面这个*要低，所以它要等*处理完后，才能再处理.

这种反转特性，使得我们考虑用栈来保存暂时未处理的操作符

再看看(A+B)*C，对应的后缀形式是AB+C*
这里+的输出比*要早，主要是因为括号使得+的优先级提升，高于括号之外的*

根据上面的“全括号”表达式，后缀表达式中操作符应该出现在左括号对应的右括号位置

所以遇到左括号，要标记下，其后出现的操作符优先级提升了，一旦扫描到对应的右括号，就可以马上输出这个操作符

总结:

在从左到右扫描逐个字符扫描中缀表达式的过程中，采用一个栈来暂存未处理的操作符
这样，栈顶的操作符就是最近暂存进去的，当遇到一个新的操作符，就需要跟栈顶的操作符比较下优先级，再行处理--->新符号和栈顶对比，新的高，就入栈（因为取时也先取）;       新的低，就把栈顶出栈，让栈顶的先运算.

利用中缀转后缀的操作流程🪂

后面的算法描述中，约定中缀表达式是由空格隔开的一系列单词(token)构成，

操作符单词包括*/+-()

而操作数单词则是单字母标识符A、B、C等。

1.首先，创建空栈opstack用于暂存操作符，空表postfixList用于保存后缀表达式

2.将中缀表达式转换为单词(token)列表

    A + B*C = split => ['A', '+', 'B', ' * ', 'C']

图解: 

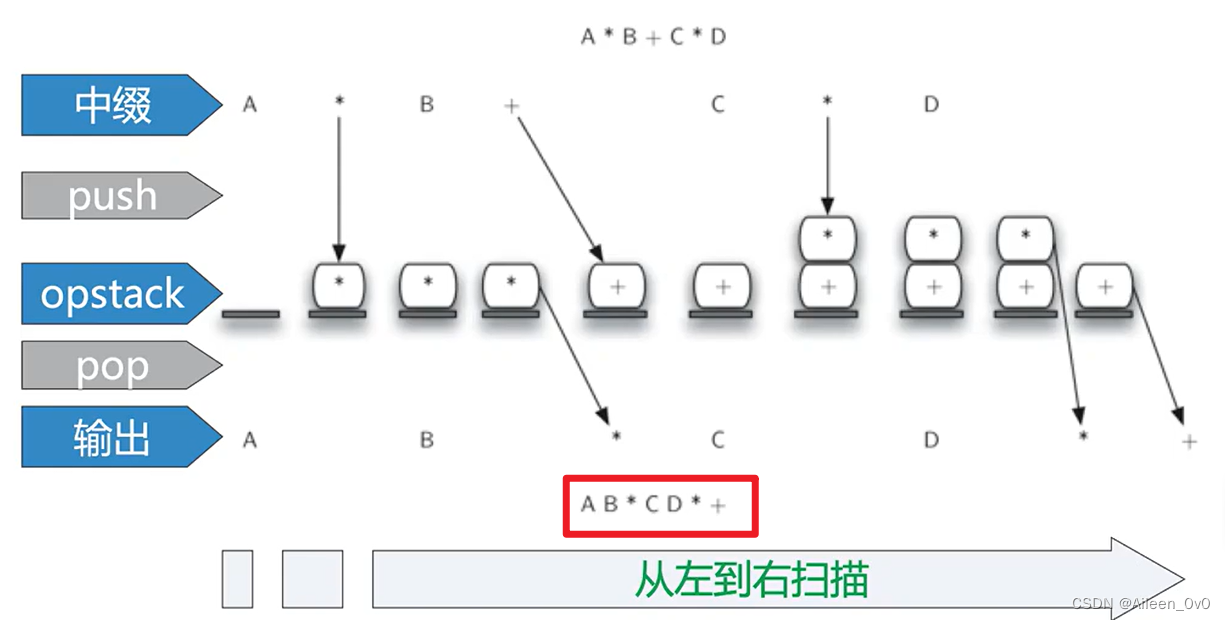
转成后缀表达式对应的代码🚀

class Stack:#Stack---->ADTdef __init__(self):self.items =[]def isEmpty(self):return self.items == []# 满足这些属性(行为)的是栈def push(self,item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[len(self.items)-1]#def size(self):return len(self.items)def infixToPostfix(infixexpr):# 记录操作符优先级prec = {}prec["*"] = 3prec["/"] = 3prec["+"] = 2prec["-"] = 2prec["("] = 1opStack = Stack()postfixList = []# 解析表达式到列表tokenList = infixexpr.split()for token in tokenList:# 操作数if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":postfixList.append(token)#  (elif token == "(":opStack.push(token)#  )elif token == ")":topToken = opStack.pop()while topToken != '(':postfixList.append(topToken)topToken = opStack.pop()# 操作符else:while (not opStack.isEmpty()) and \(prec[opStack.peek()] >= prec[token]):postfixList.append(opStack.pop())opStack.push(token)while not opStack.isEmpty():#  操作符postfixList.append(opStack.pop())#  合成后缀表达式字符串   return " ".join(postfixList)
print(infixToPostfix("A + B * C "))

运行代码测试结果 :