一、并查集的概念
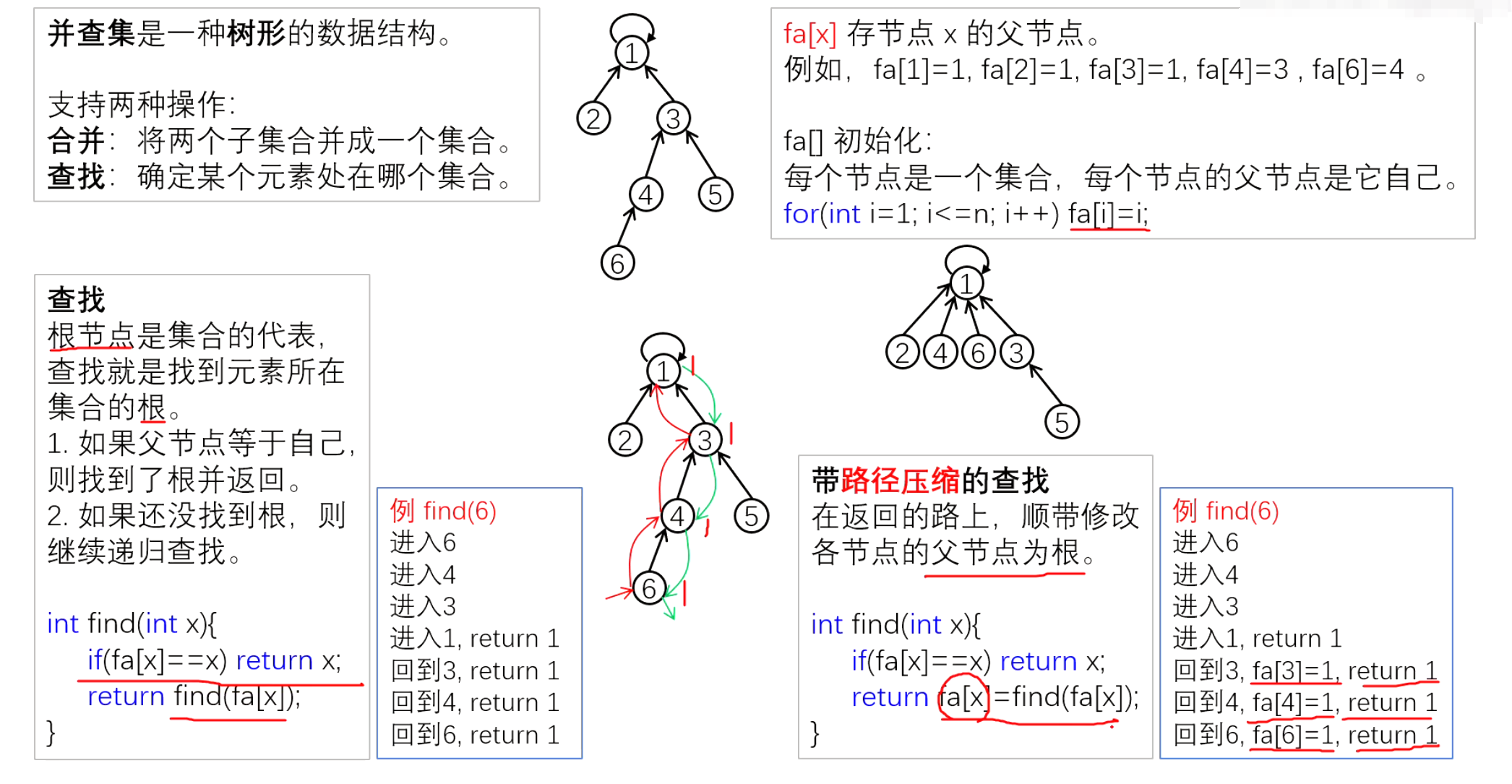
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
最裸并查集:
- 合并元素a和元素b 所在的集合。
- 查询元素a和元素b 是否属于同一组。是否在一个集合当中 ,近乎 O(1) 时间内支持两个操作
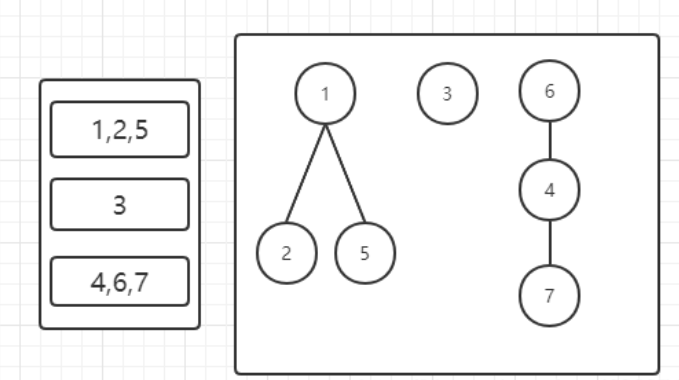
分组和对应的例子
二、并查集的结构
并查集是树形结构。不过,不是二叉树。
每个元素对应一个节点,每个组对应一颗树。
在并查集中,哪个节点是哪个节点的父亲以及树的形状等信息不用关注,整体是树形结构才最重要
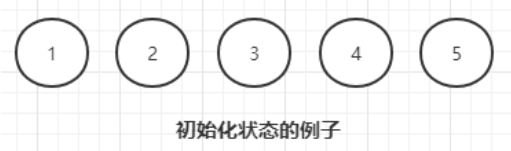
1. 初始化
每个元素初始化时,分别是每一个集合的根节点 p[x] = x
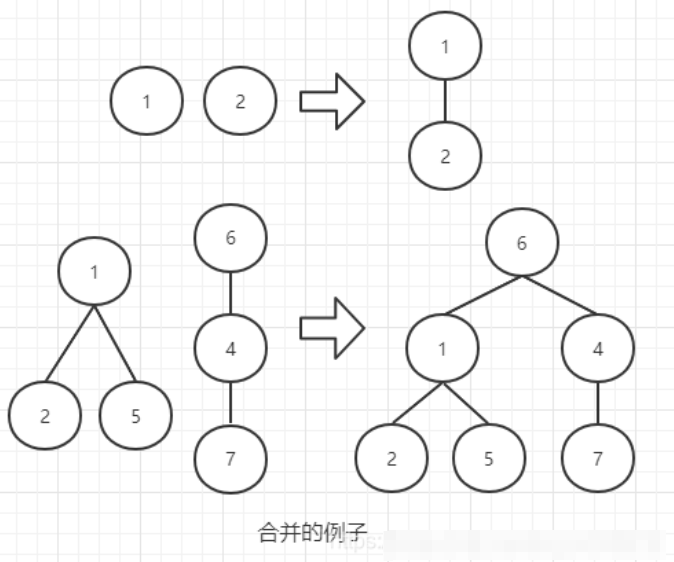
2. 合并
和下面图一样,从一个组的根向另一个组的跟连边,将两棵树变成 一颗树,也就是两个组变成一个组
3. 查询
为了查询两个节点是否同一组,只要沿着树向上走,查询根节点是否相同,根节点相同时同一组,否则不同组。如上图中 (2)(5)的根是 (1),而(7)的根是(6) 所以(2)和(5)是同一组,但是(2)和(7)不是同一组。
并查集实现的注意点
在树形数据结构中,如果发生退化情况(二叉树退化为一维链表),那么时间复杂度会变的很高。在并查集中,只需按照如下方法就可以避免退化。
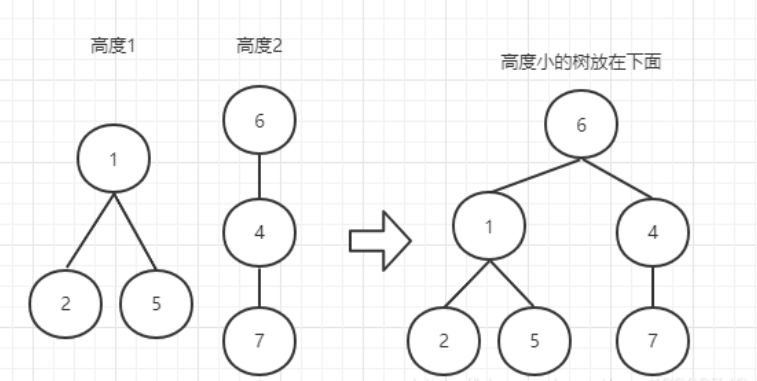
- 对于每棵树,记录树的高度(rank)
- 合并时,如果两棵树的rank不同,那么rank小的向rank大的连边。
此外,通过路径压缩,可以使并查集更高效率。对于每个节点,一旦向上走到了一次根节点,就把这个点到父亲的边改成为直接连向根。
如需要查询(7),就可以直接将(7)连接到根上。
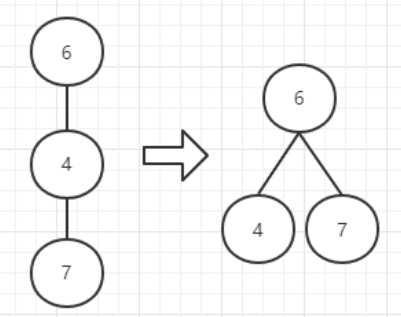
在此之上,不仅查询的节点,所有在查询过程中经过的所有节点,都可以直接连接到根上。再次查询时,就可以很快查询到根是谁了。
如下,将(2)(3)(4)(5)都连接到(1)中。
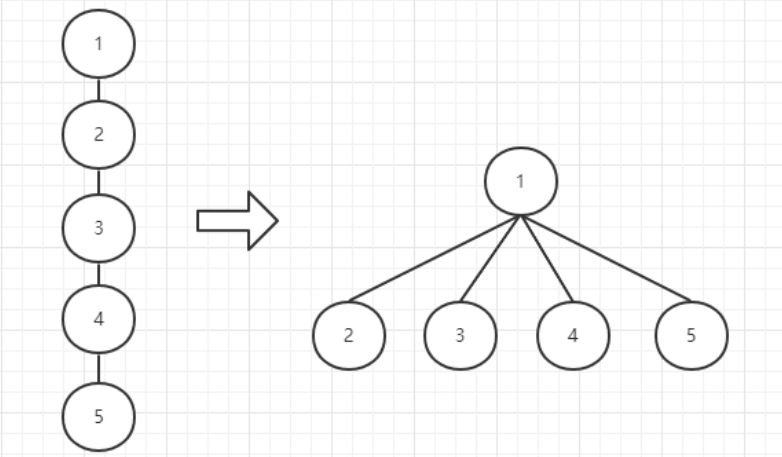
在使用这种化简方法时,为了简单起见,即使树的高度发生变换,也不再修改rank。
查并集的复杂度
加入两个优化后,查并集的效率非常高。对n个元素的查并集进行一次操作的复杂度为O(a(n))。在这里a(n)时阿克曼(Ackermann)函数的反函数。这要比O(log(n))还要快。
不过,这是“均摊复杂度”。并不是每次都满足,多次后,平均每次复杂度。
并查集的实现
Acwing 836 合并集合
#include <iostream>
using namespace std;const int N = 100010;int n, m;
int p[N];int find(int x) // 返回x的祖宗节点 + 路径压缩
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{scanf("%d%d", &n, &m);for(int i = 1; i <= n; i ++) p[i] = i;while(m --){char op[2];int a, b;scanf("%s%d%d", op, &a, &b);if(op[0] == 'M') p[find(a)] = find(b);else{if(find(a) == find(b)) puts("Yes");else puts("No");}}return 0;
}