💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

💥1 概述

📚2 运行结果

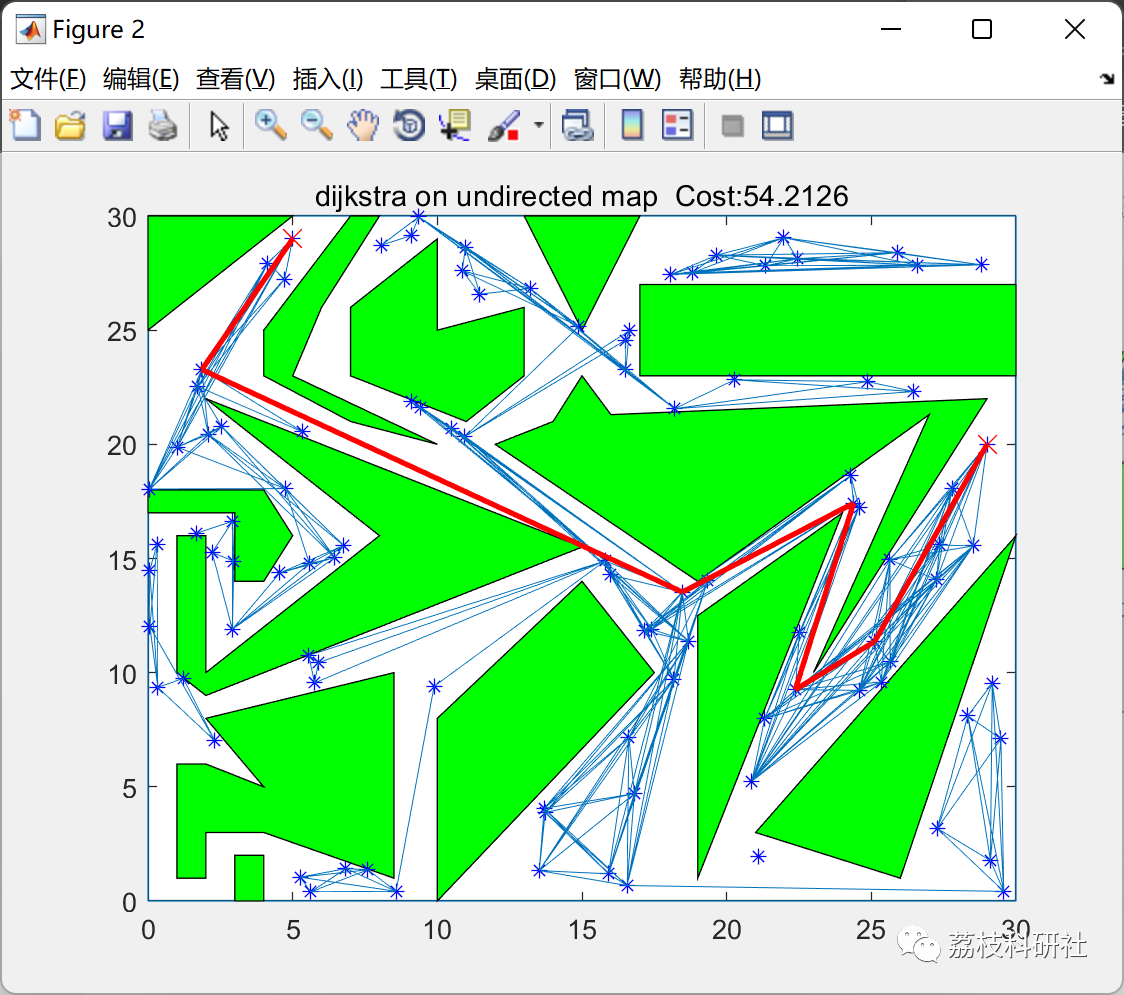
📝2.1 Dijkstra算法

📝2.2 A*算法

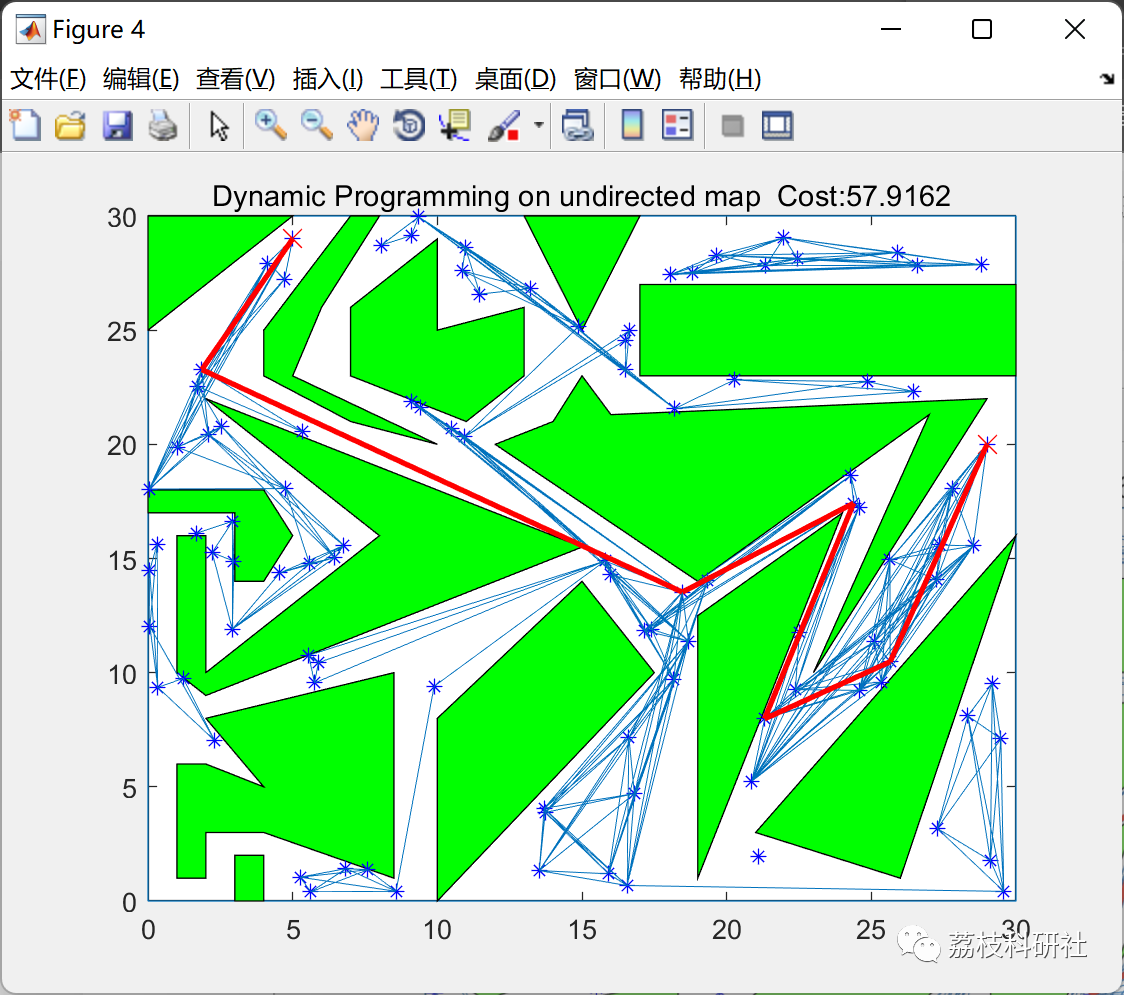
📝2.3 动态规划

🎉3 Matlab代码实现

---

💥1 概述

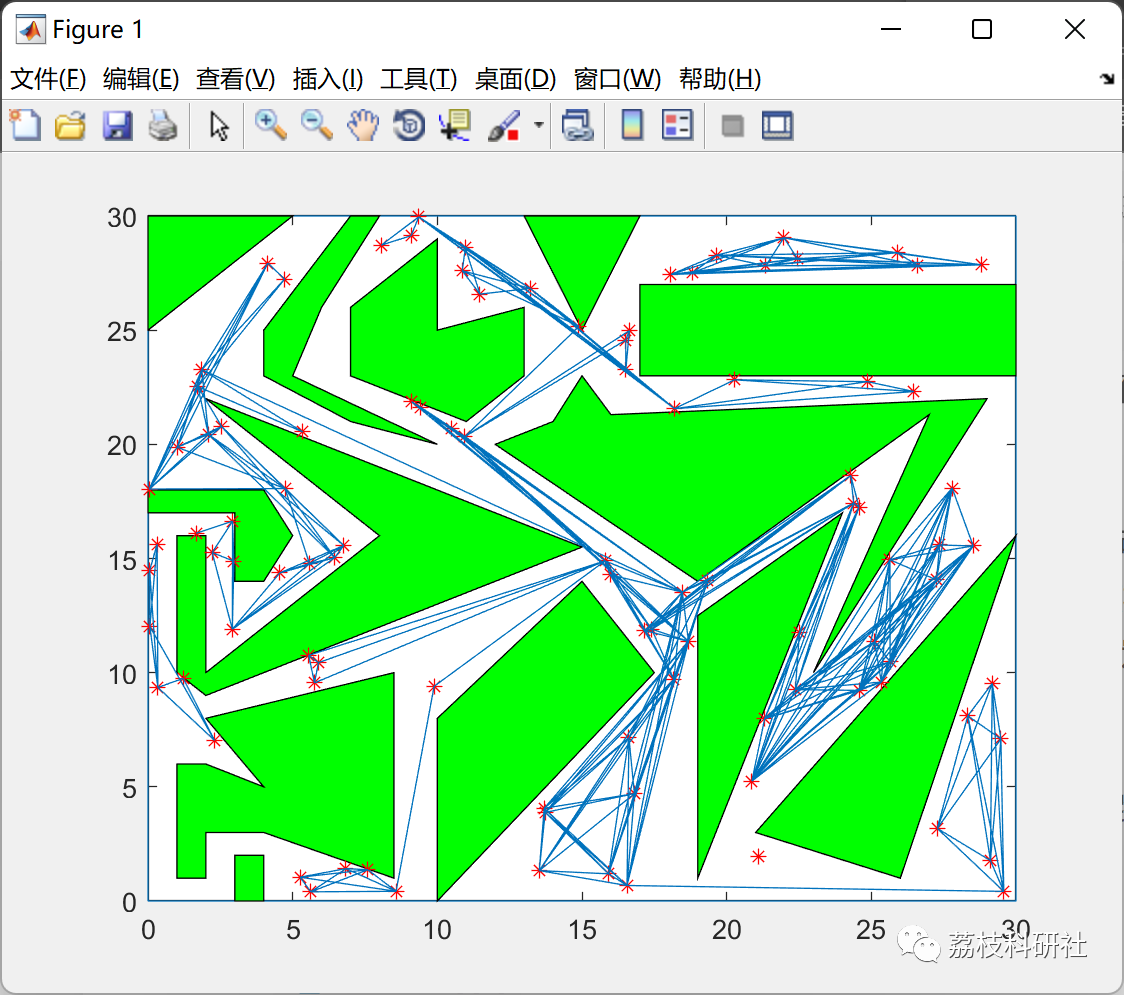
     在基于采样的方法中，需要在落在给定地图的未占用区域的地图上生成一定数量的点。然后，我们计算哪个节点与哪些节点有连接。通过这种方式，获得了生成的随机点的无向图。

    为了生成这些点，可以使用一些复杂的方法来尽可能聪明地在地图周围分布节点。但是在那个存储库中，选择通过均匀随机来生成它们。生成了100个节点，这些节点位于地图的自由区域。有给定的映射，生成的节点及其连接。

      通过Dijkstra、Astar和动态规划测试了102个节点图路径规划。

在移动机器人路径规划中，Dijkstra、A*和动态规划是常用的算法。

1. Dijkstra算法：这是一个非常基础的图搜索算法，常用于寻找两点之间的最短路径。Dijkstra算法的主要缺点是它不考虑任何关于目标的信息，因此可能会扩展很多不必要的节点。
2. A*算法：A算法是一种更高级的图搜索算法，使用了启发式函数来指导搜索。A算法通过预估函数评估搜索的方向，从而加快找到目标的速度。A*算法的主要优点是它可以快速找到最短路径，但是在复杂的环境中，预估函数的选择可能会影响到搜索的效果。
3. 动态规划：动态规划是一种优化技术，通常用于解决可以通过优化子问题来解决的问题。在路径规划问题中，动态规划可以用来寻找最优路径，但是在高维度的状态空间中，动态规划的复杂度可能会非常高。

对于移动机器人的路径规划问题，通常是在一个给定的环境地图中寻找从起始点到目标点的最优路径。这个问题可以通过将地图表示为一个图，然后使用Dijkstra、A*或动态规划来解决。每个节点可以代表地图中的一个位置，边可以代表从一个位置到另一个位置的移动。每个边的权重可以代表移动的成本，比如距离或者能量消耗。

具体选择哪种算法取决于具体的问题和需求。例如，如果需要快速找到最短路径，A*算法可能是一个好的选择。如果需要考虑更复杂的约束，比如机器人的运动能力或者环境的动态变化，可能需要使用动态规划。

Dijkstra算法、A*算法和动态规划都是常用的路径规划算法，它们可以用于移动机器人路径规划。

Dijkstra算法是一种广度优先搜索算法，用于求解带权重的图中的最短路径。它通过不断更新起点到各个节点的最短路径，并选择距离最短的节点作为下一个位置，直到找到终点或者遍历完所有节点。Dijkstra算法适用于无障碍物的静态环境。

A*算法是一种启发式搜索算法，结合了广度优先搜索和启发式函数，用于求解图中的最短路径。它通过维护一个开放列表和计算每个节点的估计代价函数（一般是距离加权和），选择代价最小的节点作为下一个位置，直到找到终点或者遍历完所有节点。A*算法适用于有障碍物的静态环境，通过启发式函数可以加快搜索速度。

动态规划是一种求解最优化问题的方法，适用于需要考虑路径中的其他因素，如时间、能量等。它通过定义状态和状态转移方程，将问题划分为子问题并求解，最终得到全局最优解。动态规划可以应对环境中的动态变化，适用于复杂的移动机器人路径规划问题。

综合应用这三种算法，可以根据具体情况选择适合的路径规划策略。例如，可以先使用A*算法进行整体路径规划，然后再使用Dijkstra算法或动态规划对细节进行优化，考虑障碍物、动态环境等因素来保证路径的安全性和效率。

📚2 运行结果

📝2.1 Dijkstra算法

📝2.2 A*算法

📝2.3 动态规划

部分代码：

function [map, nodelocation]= generate_node(map,nnode)

% merge vertices of all obstacle
obsx=map.pgx{1};
obsy=map.pgy{1};
for i=2:length(map.pgx)
    obsx=[obsx NaN map.pgx{i}];
    obsy=[obsy NaN map.pgy{i}];
end
map.obsx=obsx;
map.obsy=obsy; 
% set nodelocation to all zero
nodelocation=zeros(nnode,2);
% generate nodes
n=1;
while (n<=nnode)
    % generate random two number in range of map's border
    rx=rand* (map.xrange(2)-map.xrange(1)) + map.xrange(1);
    ry=rand* (map.yrange(2)-map.yrange(1)) + map.yrange(1);
    state=0;
    % if this node is not inside any obstacle
    if ~inpolygon(rx,ry,obsx,obsy)
        % add this location to nodelocation list
        nodelocation(n,1)=rx;
        nodelocation(n,2)=ry;
        n=n+1;
    end
end
hold on;
plot(nodelocation(:,1),nodelocation(:,2),'r*');
hold off;

🎉3 Matlab代码实现