目录

1.最大似然估计的概念的理解1

2.最大似然估计的概念的理解2

3.最大似然估计的概念的理解3

4.例子

---

1.最大似然估计的概念的理解1

        最大似然估计是一种概率论在统计学上的概念，是参数估计的一种方法。给定观测数据来评估模型参数。也就是模型已知，参数未定。已知某个随机样本满足某种概率分布，但是其中具体参数不太清楚，参数估计通过若干次的实验，观察其结果，利用结推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆值把这个参数作为估计的真实值。
        最大似然估计是建立在最大似然原理的基础上。最大似然原理：设一个随机实验有若干个可能出现的结果A1、A2、…、An，在一次实验中，结果Ak出现，则认为实验Ak的出现最有利，即Ak出现概率较大。这里用到概率最大概率最可能出现的直观想法，然后对Ak出现的概率公式求极大值，这样便可解未知参数。

最大似然估计定义：最有可能的情况（即找出与样本分布最接近的概率分布模型）

似然函数：它是一种关于统计模型中的参数的函数，表示模型参数的似然性(likelyhood)，“似然性”它 与 ("或然性"或 “概率性”或”概率“)意思相近，都是指事件发生的可能性。但是 似然性 和 概率 在统计学中还是有明确的区分：
概率：在参数已知的情况下，预测观测结果；
似然性：在观测结果已知的情况下，对参数进行估值和猜测。

 

2.最大似然估计的概念的理解2

        最大似然估计(Maximum Likelihood Estimation)是一种可以生成拟合数据的任何分布的参数的最可能估计的技术。它是一种解决建模和统计中常见问题的方法——将概率分布拟合到数据集。

        例如，假设数据来自泊松(λ)分布，在数据分析时需要知道λ参数来理解数据。这时就可以通过计算MLE找到给定数据的最有可能的λ，并将其用作对参数的良好估计。

        MLE是用于拟合或估计数据集概率分布的频率法。这是因为MLE从不计算假设的概率，而贝叶斯解会同时使用数据和假设的概率。MLE假设在计算方法之前，所有的解决方案(分布的参数)都是等可能的，而贝叶斯方法(MAP)不是这样，它使用了关于分布参数的先验信息。

        MLE之所以有效，是因为它将寻找数据分布的参数视为一个优化问题。通过最大化似然函数，找到了最可能的解。

3.最大似然估计的概念的理解3

最大似然估计把抽这些样本的每一次抽取看成一个个独立的事件，然后将它们的概率密度乘起来视为一个整体事件A，然后反推“参数为什么值的时候，事件A最有可能发生” 

4.例子

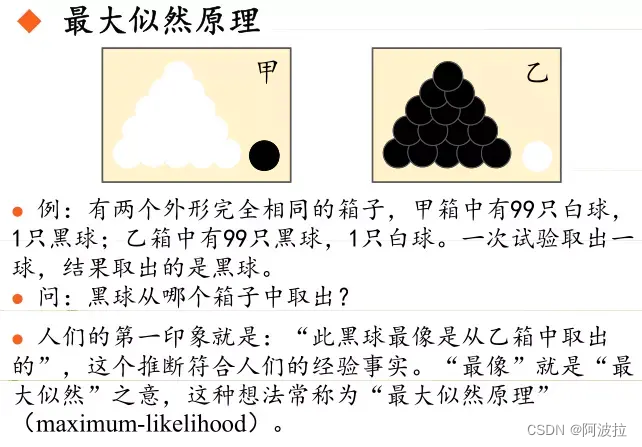
假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我们想知道罐中白球和黑球的比例，现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球再放回罐中。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？

很多人马上就有答案了：70%。而其后的理论支撑是什么呢？

我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜色服从同一独立分布。

那么问题来了，既然有无数种分布可以选择，极大似然估计应该按照什么原则去选取这个分布呢？

如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样，我们可以得到如下表达式：

P(样本结果|Model)

　　= P(x1,x2,…,x100|Model)

　　= P(x1|Mel)P(x2|M)…P(x100|M)

　　= p^70(1-p)^30.

答：采取的方法是让这个样本结果出现的可能性最大，也就是使得p^70(1-p)^30值最大，那么我们就可以看成是p的方程，求导即可！

那么既然事情已经发生了，为什么不让这个出现的结果的可能性最大呢？这也就是最大似然估计的核心。

我们想办法让观察样本出现的概率最大，转换为数学问题就是使得：

p^70(1-p)^30最大，这太简单了，未知数只有一个p，我们令其导数为0，即可求出p为70%，与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。

求最大似然估计的问题，就变成了求似然函数的极值问题。