3330:【例56.1】 和为给定数
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 625 通过数: 245
【题目描述】
现给出若干个整数,询问其中是否有一对数的和等于给定的数。
【输入】
共三行:
第一行是整数nn(0<n≤100,000),表示有n个整数。
第二行是nn个整数。整数的范围是在 0 到2×10^8之间。
第三行是一个整数m(0≤m≤2^30),表示需要得到的和。
【输出】
若存在和为 m 的数对,输出两个整数,小的在前,大的在后,中间用单个空格隔开。若有多个数对满足条件,选择数对中较小的数更小的。若找不到符合要求的数对,输出一行"No"。
【输入样例】
4
2 5 1 4
6
【输出样例】
1 5
思路:
我们可以很轻松地想到一种非常暴力的方法:套两层循环
具体是这样的:
#include<bits/stdc++.h>
using namespace std;
int main(){long long n;cin>>n;long long a[n+10];for(int i=1;i<=n;i++){cin>>a[i];}long long m,mi=INT_MAX,ma=INT_MIN;//mi和ma存储答案 cin>>m;/*循环是这样枚举的:枚举i和ji从1到n,j从1到n判断a[i]+a[j]等不等于m非常的低效!时间复杂度是O(n^2)!!! 更具体的说:比如i循环到1了,那我们就循环j,看a[1]+a[j]等不等于m要是找到了,不能确定最小数是不是最小,还要往下找要是没找到,也要继续玩下找*/for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j){long long jl=a[i]+a[j];if(jl==m&&min(a[i],a[j])<mi){mi=min(a[i],a[j]);//我们不能确定我们是不是找到最小的数,所以要用到mi和ma ma=max(a[i],a[j]);}}}}if(mi!=INT_MAX){//如果mi和原来的数一样,说明没找到 cout<<mi<<" "<<ma;//输出答案 }else{cout<<"No";//输出no }return 0;
}这个代码效率也是非常高啊,不出意外地超时了

那能优化吗?
当然可以!我们原来的代码的时间复杂度是O(n^2),这是因为代码一定要跑完两层循环,才能确定我们有没有找到最小数最小的两个数,为什么要跑玩循环?因为题目给出的数字是没排序的!我们找到两个数后,不能确定是不是最小
那我们排序一下不就好了?
#include<bits/stdc++.h>
using namespace std;
int main(){long long n;cin>>n;long long a[n+10];for(int i=1;i<=n;i++){cin>>a[i];}sort(a+1,a+n+1); long long m,mi=INT_MAX,ma=INT_MIN;cin>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j){long long jl=a[i]+a[j];if(jl==m){cout<<min(a[i],a[j])<<" "<<max(a[i],a[j]);//因为我们经过了排序,所以我们可以保证最小数是a[i],显然,后面找到的数都会比a[i]大//所以可以直接输出 return 0;//结束程序 }}}}cout<<"No";//如果能运行到这里,说明没找到,直接输出no return 0;
}
还是错了一个点!!!
那现在呢?
c++加速方法大全_ptyz306的博客-CSDN博客
将加速的代码提交上去

啊啊啊啊啊啊啊啊啊啊,凭什么!!!😡🤬
看来只能乖乖优化算法了🤔
我想到了一个新方法:
还是循环i,然后定义一个变量b,b=m-a[i],现在,我们只需要知道数组中有没有b就行了
那我们怎么知道呢?
lower_bound(a+1,a+n+1,b)-a;
这句代码可以找到在a数组的1-n号下表中,有没有数字大于等于b,并返回这个数字的位置
非常智能啊,这样,我们就可以把代码优化成这样:
最终代码:
#include<bits/stdc++.h>
#pragma GCC optimize(3)
using namespace std;
inline int read(){//快读int x=0,w=0;char ch=0;while(!isdigit(ch)){w|=ch=='-';ch=getchar();}while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}return w ? -x : x;
}
inline void write(int x){//快写if(x<0)putchar('-'),x=-x;if(x>9)write(x/10);putchar(x%10+'0');
}
int main(){long long n,m;n=read();long long a[n+10];for(int i=1;i<=n;i++){a[i]=read();}sort(a+1,a+n+1); m=read();for(int i=1;i<=n;i++){long long b=m-a[i];long long wz=lower_bound(a+1,a+n+1,b)-a;//找到b的位置 if(b==a[wz]){//如果找到的位置上的数和b一样,说明我们找到了 cout<<a[i]<<" "<<a[wz];//果断输出 return 0;//结束程序 }}cout<<"No";return 0;
}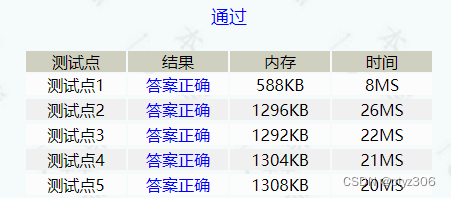
终于过了!!!不容易啊