数学建模Matlab之基础操作

作者由于后续课程也要学习Matlab，并且之前也进行了一些数学建模的练习（虽然是论文手），所以花了几天零碎时间学习Matlab的基础操作，特此整理。

基本运算

a=5+5 %加法，同理减法
b=2^3  %立方
c=5*2 %乘法
x = 1; %分号用于不显示，这样在命令行窗口就没有任何输出
y = x + 5
eps %浮点数的相对误差
1i^2 %虚数
pi

1.原来；不是可有可无的，只要写上；就代表在命令行窗口中不产生输出

2.虚数也可以是ly

变量和向量

%% 变量
% 输入，如果输入的不是正确格式，则继续接收，直到格式正确
x=input('请输入数字：');
y=x*2% 数据显示格式
% 修改数据显示格式
format long ,pi % 可以修改为小数点后16位
format  short ,pi % 默认short formal，四个小数位
% 定义时指定数据显示格式
format short %直接声明为短型
a=3.1415926a=5
b=2
a>b %大于
a==b %等于
a<b %小于
% 如果为真，则返回1，否则返回0

%% 向量
% 冒号创建，开始：步长：结尾
x=2:2:10% linspace函数创建线性间隔变量，（开始，结束，元素个数）
y=linspace(1,20,10)a=[1 2 3 4 5]; % 一行矩阵，可以看成是向量的一部分
b=[6 7 8 9 10];
c=a.*b % 加上. 就表示元素之间的运算
sum(c) % 将c向量的所有元素求和d=dot(a,b) % 使用dot函数对两个向量进行点积，就是x1y1+x2y2……+xnyn这个和的结果a=[1 2 3 ];
b=[6 7 8 ];
c=cross(a,b) % 三维向量的交叉积，右手法则从a到b就是c的方向pause %用于暂停指令，下面的指令暂时不会执行

其中，y=linspace()是一个较为常见的创建线性变量的方法。

矩阵

基础的不讲，首先是矩阵。

%% 矩阵
A=[1 2 3; 4 5 2; 3 2 7]
A=[1 2 3 4 5 2 3 2 7]
B=A' %把A进行转置，行变列，列变行
C=A(:) %从左到右，从上到下，竖向展示矩阵的内容

多种矩阵定义中，作者感觉第二种较为常见，层次很分明。很少见到A(:)展示，A‘注意是转置。

D=inv(A) %求矩阵的逆矩阵，注意，只有非奇异矩阵（行列式值不为0）才能求逆矩阵
A*D %A乘A的逆，就是单位矩阵E

注意：inv(A)是逆矩阵，非常常见。并且一定要注意的是，只有非奇异矩阵（即对应行列式不为0）才能有逆矩阵！那么，如何才能快速求得某一个方阵对应行列式值呢？方法如下：

det_A = det(A)
F=[1,2,3;4,5,6;7,8,9]
det_F = det(F) %在实际的数值计算中，由于浮点数的表示和计算误差，得到一个非常接近于0的行列式是可能的。

对于上文的A矩阵，可以得到det_A=-34，很明显不为0；对于新建的F矩阵，可以得到det_F为：

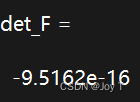
这……这已经很接近于0了，那它到底等不等于0啊？

原来，在实际的数值计算中，由于浮点数的表示和计算误差，得到一个非常接近于0的行列式是可能的。通常使用一些容差值来决定是否将计算出的行列式值视为0，本质上就相当于设置一段趋近于0的区间，只要行列式结果位于这个区间，就认为求得的行列式值为0，即对应方阵为奇异矩阵，没有逆矩阵。

tol = 1e-10;
if abs(det_F) < toldisp('F 是奇异矩阵');
elsedisp('F 不是奇异矩阵');
end

后续可以考虑封装为函数，通过这个流程，我们就可以对F矩阵是否能求逆矩阵进行判断：

然后是创建随机矩阵，作者目前这几天还没遇到过使用它的情况：

E=zeros(10,5,3) %创建一个10行5列3维的全0矩阵，原来3表示3维%%伪随机数（伪随机矩阵生成）
E(:,:,1) = rand(10,5) %rand(m,n)生成m行n列的均匀分布的伪随机数矩阵
%rand(m,n,‘double’)生成指定精度的均匀分布的伪随机数，参数还可以是’single’，默认情况下rand生成的全是整数randi(10) %开区间0~10，貌似只能生成整数E(:,:,2) = randi(5,10,5) %参数1界定最大范围。
E(:,:,2) = randi([1,6],10,5) %参数1也可以用两个数表示一个区间

另外补充一些矩阵的常见使用：

A = [1,2,3,4,5,6,5,4,6] % 没有;分割，就是一整行
B = 1:2:9 %第二个参数为步长，不可缺省，1 3 5 7 9 
B = 1:3:9 % 1 4 7
C = repmat(B,3,2) %以B矩阵为元素，生成3行2列的新的矩阵
D = ones(2,4) %生成一个2行4列的全1矩阵

其实通过B=1:9来获得行向量，还是较为常见的。作者在后续定义初始路径时，使用的就是这样的定义方法。zeros(2,3)或者ones(2,3)都是一种类型，使用固定的常量定义矩阵。

然后就是矩阵及其元素的四则运算，普通的*对应的就是矩阵的乘法，若使用.*或者./，那么涉及到的就是矩阵对应元素之间的运算了（别忘了矩阵相加减是矩阵元素相加减哦！）：

% 矩阵及其元素的四则运算
A = [1 2 3 4; 5 6 7 8]
B = [1 1 2 2; 2 2 1 1]
C = A + B
D = A - B
E = A * B' %注意这个是‘转置
F = A .* B % .*表示对应元素相乘，不是矩阵的乘法
G = A / B % 相当于A*B的逆，逆矩阵是inv(B)
G = A \ B % 相当于B*A的逆
H = A ./ B % ./表示对应项相除

在实际操作过程中，矩阵转置对于初学者实在是不好区分，明明正确表述就是 $B^T$ ，Matlab非要写成逆矩阵B'的形式……初学者们一定要注意哈！逆矩阵是inv()函数得到的，即inverse matrix。

% 矩阵的下标
A = magic(5)
% magic幻阵：数字是从1到n^2 的整数，并且每一行、每一列以及主对角线和副对角线上的数字之和都相等。
% 幻阵常用于密码学、设计与艺术、数学研究和解决某些优化和排列问题
B = A(2,3) %取矩阵二行三列元素值
C = A(3,:) % :为取全部,那么这条语句表示取第三行
D = A(:,4) %取第四列
[m,n] = find(A > 20) %找到大于20的序号值/矩阵
%取的是索引值，n是行，m是列

这里取元素值蛮重要，A(2,3)就是取矩阵A二行三列的元素，：表示全部，相当于占位符*。

元胞数组

Matlab的元胞数组（cell array）是一种特殊的数组类型，它可以容纳不同类型和大小的数据。与常规数组不同，每个元胞可以包含任何类型的数据。

{ }法

C = {'text', [1, 2, 3], 5}; %这里，C 是一个包含三个元胞的元胞数组。
% 第一个元胞包含一个字符串，第二个元胞包含一个向量，第三个元胞包含一个标量。C{1} % 返回 'text'
C{2} % 返回 [1, 2, 3]
C{3} % 返回 5
C{1} = 'new text'; % 修改第一个元胞的内容

通过{ }创建元胞数组，比较简单，推荐使用。调用元素时注意一定不是平常数组的（）方法，而是同样需要{ }进行元素调用。可以对元胞数组进行简单的函数操作（简单看看就行）：

% 使用 cellfun 函数来对每个元胞应用函数
result = cellfun(@length, C); % 返回每个元胞的长度：8，3，1% 可以使用 cellfun 和匿名函数来计算每个向量的和：
C = {[1, 2, 3], [4, 5], [6, 7, 8, 9]};
sums = cellfun(@(x) sum(x), C); %sums 是一个数组，其中包含 C 中每个向量的和。%使用循环来操作元胞数组的内容，显示 C 的每个元胞的内容。
for i = 1:length(C)disp(C{i});
end

cell( )法

%% 元胞数组2
A = cell(1,6) %这行代码创建了一个1行6列的空元胞数组A。
A{2} = eye(3) %将一个3x3的单位矩阵赋值给A的第2个元素。
A{5} = magic(5) %将一个5x5的幻方矩阵赋值给A的第5个元素。
B = A{5}

通过cell函数创建的元胞数组，如果数组中的元素比较少，建议使用{ }，直接初始化。但是如果元素比较多，那作者认为使用cell先创建空元胞数组应该是更好地办法吧！

结构体

在MATLAB中，结构体（或称为“结构”）是一种数据类型，它允许将多个不同类型的数据组合在一起。结构体中的每个数据项都被称为字段，每个字段都有一个与之相关的字段名。

作者爱用的定义

student.name = '张三';
student.age = 20;
student.grade = '三年级';

就这么简单！定义都不定义，直接加.表示前者就是结构体，后者就是字段。运行结果如下：

对于多个同一类型的结构体（比如不同的班级），可以进行如下定义：

class(1).name = '张三';
class(1).id = '001';
class(1).scores = [95, 88, 76];class(2).name = '李四';
class(2).id = '002';
class(2).scores = [89, 92, 85];

哇去，简直是清晰明了啊！

长得像C语言的定义

books = struct('name',{{'Machine Learning','Data Mining'}},'price',[30,40]) %包含两个字段：name 和 price。
% 为结构体的某个字段分配一个元胞数组，你需要使用双大括号 {{}}。books.name %访问结构体的字段
books.name(1)
books.name{1}

这就有的讲了，上述代码设置books为结构体，其中有两个字段：name 和 price。以一个字段一个值这个顺序定义的，是不是不难理解？

读者可能会发现，这name后面，怎么跟了{{ }}？难道我在学vue在这传递变量了？其实，在结构体定义中，如果要为字段赋元胞数组类型的值，那么这个元胞数组就不能是原本的{ }，必须要嵌套两层{{ }}才能表示这是个元胞数组，不信，你看上述代码执行的结果：

name(1)和name{1}有什么不同呢？不是说元胞数组调用元素使用的是{ }吗？不妨我们运行一下：

糟了，要长脑子了：

books.name(1) 返回的是name字段中的第一个元素的单元格，而不是单元格中的实际内容。因此，返回的是一个包含'Machine Learning'的1x1元胞数组。

books.name{1} 通过使用花括号 {} 来索引元胞数组，可以直接访问单元格中的实际内容。因此，这将返回字符串 'Machine Learning'。

扩展

既然结构体中赋值元胞数组需要{{ }}，那么作者想，使用{ }给name赋值会出现什么情况呢？

books_single = struct('name',{'Machine Learning','Data Mining'},'price',[30,40])
books_single(1).name
books_single(1).price
books_single(2).name
books_single(2).price

结果：

欸，变成1*2的结构体数组了！这是怎么回事呢？其实，这是matlab的规定，如果是单个{}，则表示将{}中的所有元素分别分配给前面的字段name。在上面的例子中，{}的两个值分别赋给name，这就使得struct有两个name，导致整个的struct变成1*2的结构体数组。

可以通过book(1)这样调用第一个结构体，第一个结构体中name被分配第一个值，第二个结构体中name被分配第二个值，此时price的值在两个结构体中是相同的。

如果同时给price分配两个数（和name一样用{}分配），那结果和作者想的不同，作者以为是笛卡尔积一共是1*4结构体数组，没想到还是1*2：

books_single2 = struct('name',{'Machine Learning','Data Mining'},'price',{[30,40],[50,60]})
books_single2(1).name
books_single2(1).price
books_single2(2).name
books_single2(2).price

所以作者认为，单独的{}本质上就是为了方便创建结构体数组的，name参数1和price参数1一起，然后按照顺序，name参数2和price参数2一起构成下一个结构体。那如果再给name增加一个数会发生什么呢？

books_single3 = struct('name',{'Machine Learning','Data Mining','Matlab'},'price',{[30,40],[50,60]})

结果报错啦！name字段是一个长度为3的字符串数组，而price字段是一个长度为2的数组的数组。这两个字段的长度不匹配，导致了错误。只能让两者长度保持一致，或者其中之一为标量值，没有{}，如上文的books_single。

% 保证结构体字段长度相同
books_single3 = struct('name',{'Machine Learning','Data Mining','Matlab'},'price',{30,40,50})
books_single3 = struct('name',{'Machine Learning','Data Mining','Matlab'},'price',{{[30,40]},{[50,60]},{[70,80]}})

与元胞数组的比较

在数学建模中的应用：

结构体:
用于存储模型的参数和配置信息。
例子: model.parameters, model.settings。
元胞数组:
用于存储不同类型或大小的数据集，例如多个数据集或多个模型。
例子: 不同类型的输入数据或模型。

如果你需要存储具有命名字段的相关数据，结构体可能更合适。
如果你只是需要存储不同类型或大小的数据，并不关心字段名称，那么元胞数组可能是更好的选择。
在数学建模中，这两种数据类型都很有用，具体的选择取决于你的具体需求和使用场景。

流程结构

%% 循环结构
sum=0;
for i=1:5sum=sum+1;
end
% 间隔也可以为负数
for a = 1.0: -0.1: 0.0disp(a)
end
% 也可以不是常见的循环结构，可以是数组，但是注意，如果之前已经赋过a的话，也需要这么写
for a = [2 3 4 5 6]disp(a)
end
% 如果a本来就有值，也不能写成 for a ... disp(a) ...end的格式，matlab会检测表达式无效% while循环
i=0;
sum=0;
while(i<10)sum=sum+i;i=i+1;
end
fprintf('累加和为： %d \n', sum);%% 分支结构
if sum==3'成立'
else'不成立'
endswitch sum>0case 1disp('sum大于零');otherwisedisp('sum小于等于0');
end

到时候看看具体算法，看多了就熟悉了。

基本绘图操作

代码来自于CSDN最火的两个matlab教程。

波形函数绘图

%% 基本绘图操作
%1.二维平面绘图
x = 0:0.01:2*pi %定义x的范围，第二个参数表示步长
y = sin(x)
figure %建立一个幕布
plot(x,y) %绘制当前二维平面图
title('y = sin(x)') %标题
xlabel('x') %x轴
ylabel('sin(x)') %y轴
xlim([0 2*pi]) % x坐标值的范围

x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
figure
[AX,H1,H2] = plotyy(x,y1,x,y2,'plot'); %共用一个x的坐标系，在y上有不同的取值
%设置相应的标签
set(get(AX(1),'Ylabel'),'String','Slow Decay')
set(get(AX(2),'Ylabel'),'String','Fast Decay')
xlabel('Time(\musec)')
title('Multiple Decay Rates')
set(H1,'LineStyle','--')
set(H2,'LineStyle',':')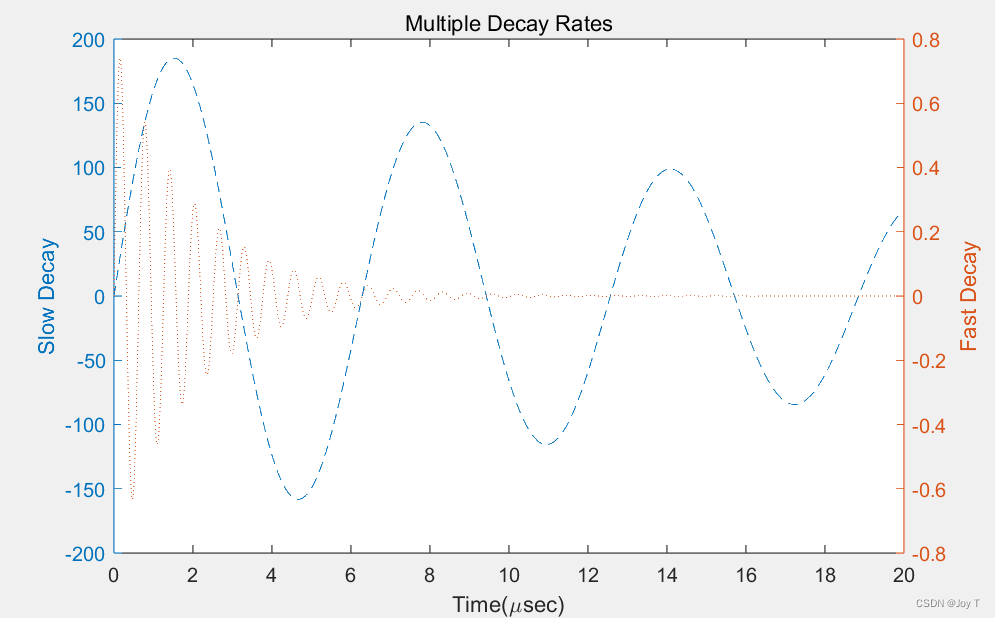

双峰函数绘图

%2.三维立体绘图
t = 0: pi/50: 10*pi;
plot3(sin(t),cos(t),t)
xlabel('sin(t)')
ylabel('cos(t)')
zlabel('t')
%hold on
%hold off %不保留当前操作
grid on %把图片绘制出来，在图片中加一些网格线
axis square %使整个图（连同坐标系）呈方体[x,y,z] = peaks(30); %peaks命令用于产生双峰函数或者是用双峰函数绘图
mesh(x,y,z)
grid

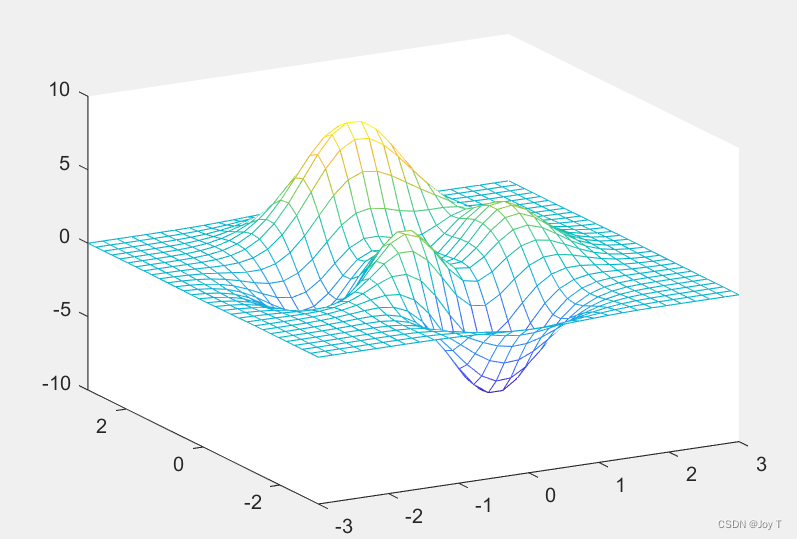
散点图

%% 数据可视化——散点图
% x表示年龄，y1表示人体血压。绘制年龄与血压的关系，使用scatter散点图函数
x=[75;78;51;82;77;88;41;78;78;61;71;74;62;81;75;64;80;72;51;80;56;73];
y1=[208;146;168;149;208;102;130;155;163;154;145;147;143;161;145;120;153;158;123;163;177;148];scatter(x,y1)
scatter(x,y1,'r')  %填充颜色绘制为红色% 利用向量配置多彩颜色，每个点的颜色由c确定。
c = linspace(1,10,length(x)); %生成了一个线性间隔的向量c。c的长度与x相同，值从1到10。
scatter(x,y1,[],c) %这些值作为颜色数据传递给scatter函数，使散点具有从一种颜色渐变到另一种颜色的效果。% 填充并标记散点彩色图
sz = 30; % 设置散点的大小为30。
c = linspace(1,10,length(x)); %同样利用向量配置多彩颜色
scatter(x,y1,sz,c,'filled') %填充散点

条形图

%% 数据可视化——条形图
x = {'计算机系统基础','汇编语言','信息安全','机器学习'}; %x个数一定要与y个数对应
y = [94,54,65,87];
%在调用 bar 函数时，MATLAB 不支持直接使用字符串数组作为 x 坐标轴标签。您可以使用类别数组 categorical 来解决这个问题。
x = categorical(x); % 将x转换为类别数组
% bar(x,y)
b = bar(categorical(x), y);
b.FaceColor = [0.5 0.7 1]; % 设置为淡蓝色 (RGB 色值)
xlabel('科目') %经过我的深思熟虑，我认为还是要保证整个图像的完整性，不要仅仅依赖于图题
ylabel('成绩')
title('成绩分布图')

函数

简单说明一下，在MATLAB中，不能在命令窗口中直接定义函数。函数必须保存在一个扩展名为.m的文件中，并且文件名必须与函数名相同。这文件的创建，左上角新建--函数，就会有对应函数模板的文件出现啦：

格式为function 输出形参表 = 函数名（输入形参表）。对于函数，要有以下保证：

1.确保文件已经正确保存，文件名与函数名匹配，且扩展名为.m（例如f.m）。
2.确保函数文件位于当前的MATLAB工作路径中，或者您在调用函数时提供了完整的文件路径。

给个例子：

% function 输出形参表 = 函数名（输入形参表）
function y = funcdemo1(x)
%UNTITLED 此处显示有关此函数的摘要
%   此处显示详细说明
%   x为一个整数
if x>0y=2*x;
elseif x==0y=0;
elsey=x*x;
end
disp(y)
end

到时候调用啊，直接调用funcdemo1(x)就行了：