初级数值计算理论总结

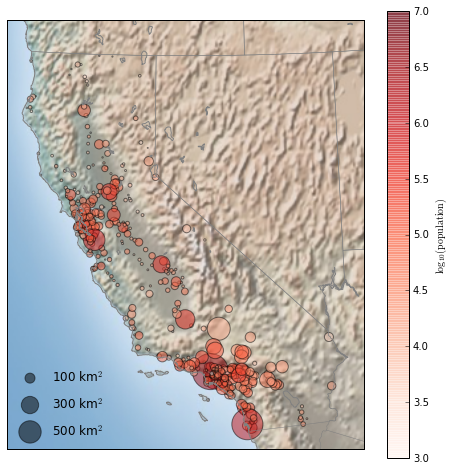
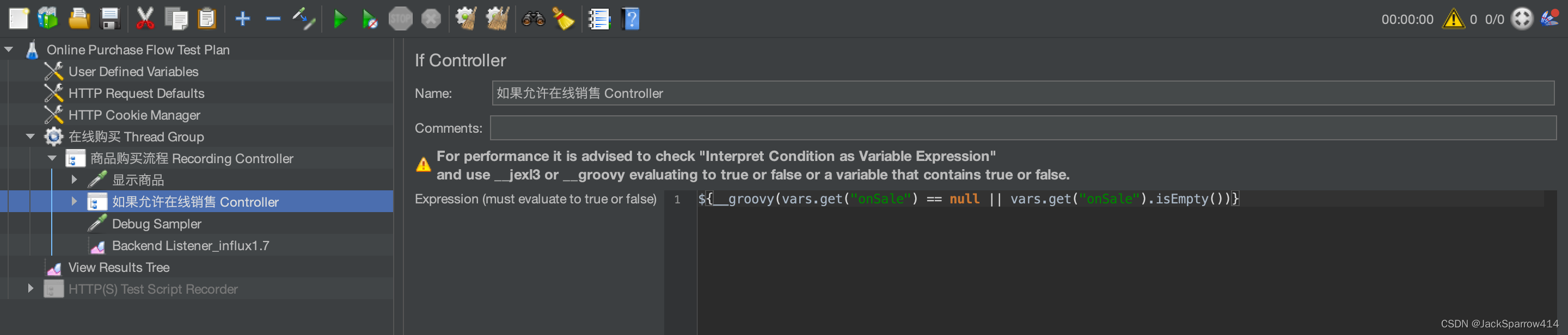
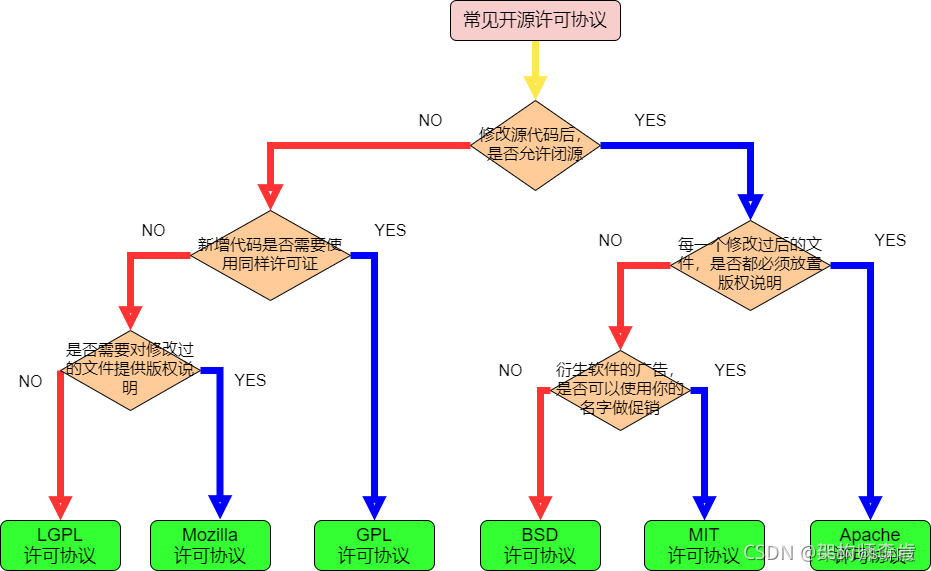
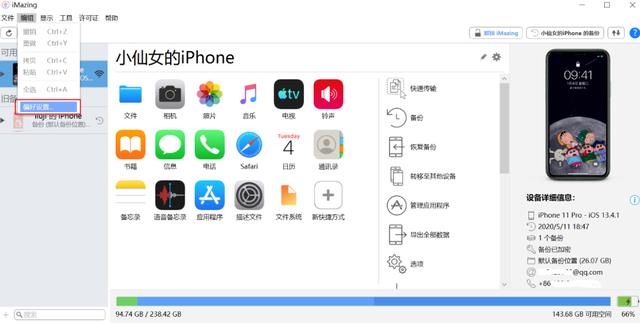
本文用于总结复习与研究生面试
- 一问，小伙子会不会数值计算啊
- 一答：会
- 二问：哦，讲讲看
- 二答：讲不出来
- 三问：......

数值求根

$f(x)=0$

二分法
Jacobi 迭代法

$x_{k+1}=g(x_k)$

Jacobi 迭代改进算法（事后加速法）（根位置 $x^*$ ）

$x_{k+1}=g(x_k)$

$x^*=g(x^*)$

$x_{k+1}-x^*=g(x_k)-g(x^*)=g'(\zeta )(x_k-x^*),\zeta \in [x_k,x^*]$

$x_{k+1}'=\frac{x_{k+1}-g'(\zeta)x_k}{1-g'(\zeta)}$

$x_{k+1}=x'_{k+1}$

Aitken 加速算法（根位置 $x^*$ ）

$x_{k+1}=g(x_k),x_{k+2}=g(x_{k+1})$

$\left\{\begin{matrix} x_{k+1}-x^*=g'(\zeta_1)\cdot(x_k-x^*) &\zeta_1\in [x_k,x^*] \\ x_{k+2}-x^*=g'(\zeta_2)\cdot(x_{k+1}-x^*) &\zeta_2\in [x_{k+1},x^*] \end{matrix}\right.$

$x'_{k+1}=x_{k+2}-\frac{(x_{k+2}-x_{k+1})^2}{x_{k+2}-2x_{k+1}+x_k}$

$x_{k+1}=x'_{k+1}$

Newton 迭代法

$x_{k+1}=g(x_k)=x_k-\frac{f(x_k)}{f'(x_k)}$

最速下降法
- 使得

$f(x)=0\rightarrow \frac{dV(x)}{dx}=0$

$V(x)=V(x_k)+\frac{dV(x_k)}{dx}(x-x_k)+O((x-x_k)^2)$

现有任意大于零的常数 $\lambda$

$x_{k+1}=x_k-\lambda f(x)$

......这种方法，反正我从来没用过

线性方程组

$Ax=y$

Gauss 消元法
- 都能实现，只讲一下要点
  - 一定要在程序设计时注意到，零除错误，总之，这种方法很依赖微操
  - 而且很受限制，如果不能完成自主的排版工作，
  - 可以设置仅求解满秩方程
LU分解法
- L：左下三角矩阵
- U：右上三角矩阵
- 事实上 $A=LU$ 所以只需要求出一个就行
- LU 分解步骤
(1)...以后补
(2)...反正
(3)...这种方法
(4)...实际中也没人用

Jacobi 迭代

$Ax=b\rightarrow (D-L-U)x=b\rightarrow x=D^{-1}(L+U)x+D^{-1}b$

$D$ 对角矩阵， $L$ 下三角矩阵， $U$ 上三角矩阵（与LU分解没有任何关系，就是单纯的相加，L，U矩阵的对角线上的值均为零）

例如：

$\begin{bmatrix} 1 & 2 &2 \\ 3 & 1 &2 \\ 3 &3 &1 \end{bmatrix}=\begin{bmatrix} 1 & & \\ & 1 & \\ & & 1 \end{bmatrix}-\begin{bmatrix} 0 & -2 & -2\\ & 0 & -2\\ & &0 \end{bmatrix}-\begin{bmatrix} 0 & & \\ -1 &0 & \\ -1 & -1 &0 \end{bmatrix}$

收敛条件是常被问到的问题：主要想偷摸问你一下矩阵的谱半径 $\rho$ （本征值的绝对值的最大值）

收敛充要条件： $\rho\leq 1$

Gauss-Seidel 迭代
- 经过数学家的微操，认为Jacobi 迭代有一些重复的步骤，这种迭代减去了这一步骤

$x_{k+1}=(D-L)^{-1}Ux_k+(D-L)^{-1}b$

类似的，判别矩阵为 $G=(D-L)^{-1}U$

- 事实上，在编程时，我们总是使用已经计算好的表达式而不是进行矩阵运算

松弛迭代法
- 这是一种类似于最速下降法的求解方法，意义很大，我将新开一篇博客专门讲这个问题

矩阵本征值计算问题

Jacobi 迭代法
- 因为有
  - 对角矩阵的特征值为对角线上的元素值
  - 矩阵的相似变换不改变矩阵的特征值
  - 已经具体介绍过，参加链接

对应博客

这一节内容极其重要，我都专门写了博客，链接贴在下面
- QR分解
- 三对角化方法
- 广义本征值问题

插值与拟合

这一节显然就没有什么特点了，就硬背吧......
- 插值：就是给一堆点，你给整一个函数，使得每一个点都在这个函数上
- 拟合：就是给一堆点，给一个含参函数，通过一些方法确定这个参数，使得这个函数与点之间的距离不要太远
  - 常用的方法
    - 最小二乘法
不会有人考这玩意的，这东西纯靠记忆力，记不住拉倒