个人主页 ： 个人主页
个人专栏 ： 《数据结构》 《C语言》《C++》《算法》

---

前言

本篇文章仅是作为小白的我的一些理解，，如果有错误的地方，希望大佬们指出。

---

• 题目链接： 34. 在排序数组中查找元素的第一个和最后一个位置
  

一、题目解析

本题数组元素不唯一，可能存在多个target，我们就是要找到target区间中的左端点与右端点。

如果没有target区间，则返回{-1, -1}

二、解题思路

1. 暴力查找

直接遍历数组，如果可以查找到target则返回第一次与最后一次遇到target的下标，如果不能查找到target则返回{-1， -1}。
时间复杂度：O(n)

2. 一次二分查找 + 部分遍历

优先使用二分查找target，如果可以查找到，就从该下标开始向左向右遍历数组，返回最左边与最右边的target。如果不能查找到，返回{-1, -1}
时间复杂度：O(logn + n)

对于{3,3,3,3,3,3,3,3} target = 3，时间复杂度会退化为O(n)

3. 两次二分查找分别查找左右端点

1.查找区间左端点

我们对示例1使用 “ 二段性 ” 可以发现示例一被target分成了两部分，小于target部分{5, 7, 7}和大于等于target部分{8, 8, 10}。

如果中点mid到小于target的部分，区间[ left, mid ]这一区间都小于target，不可能是target区间的左端点，那么left = mid + 1；
如果中点mid到大于等于target的部分，区间[ mid, right ]这一区间都大于等于target， 其中mid有可能是target区间的左端点，那么right = mid；

---

细节处理：

• 循环条件：left < right
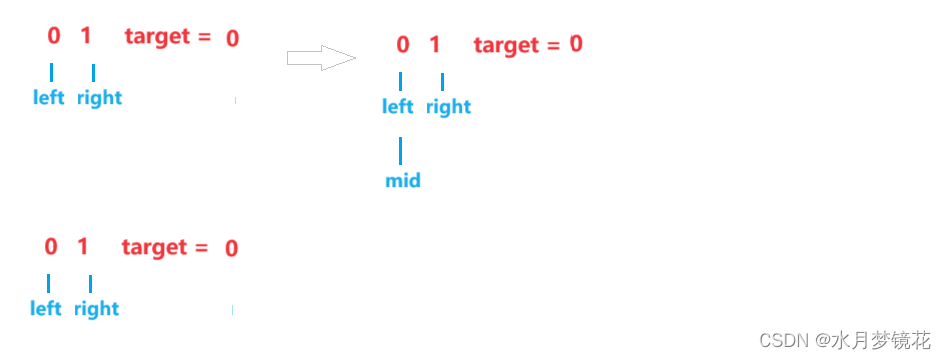
  如果循环条件为left <= right就会死循环。
  

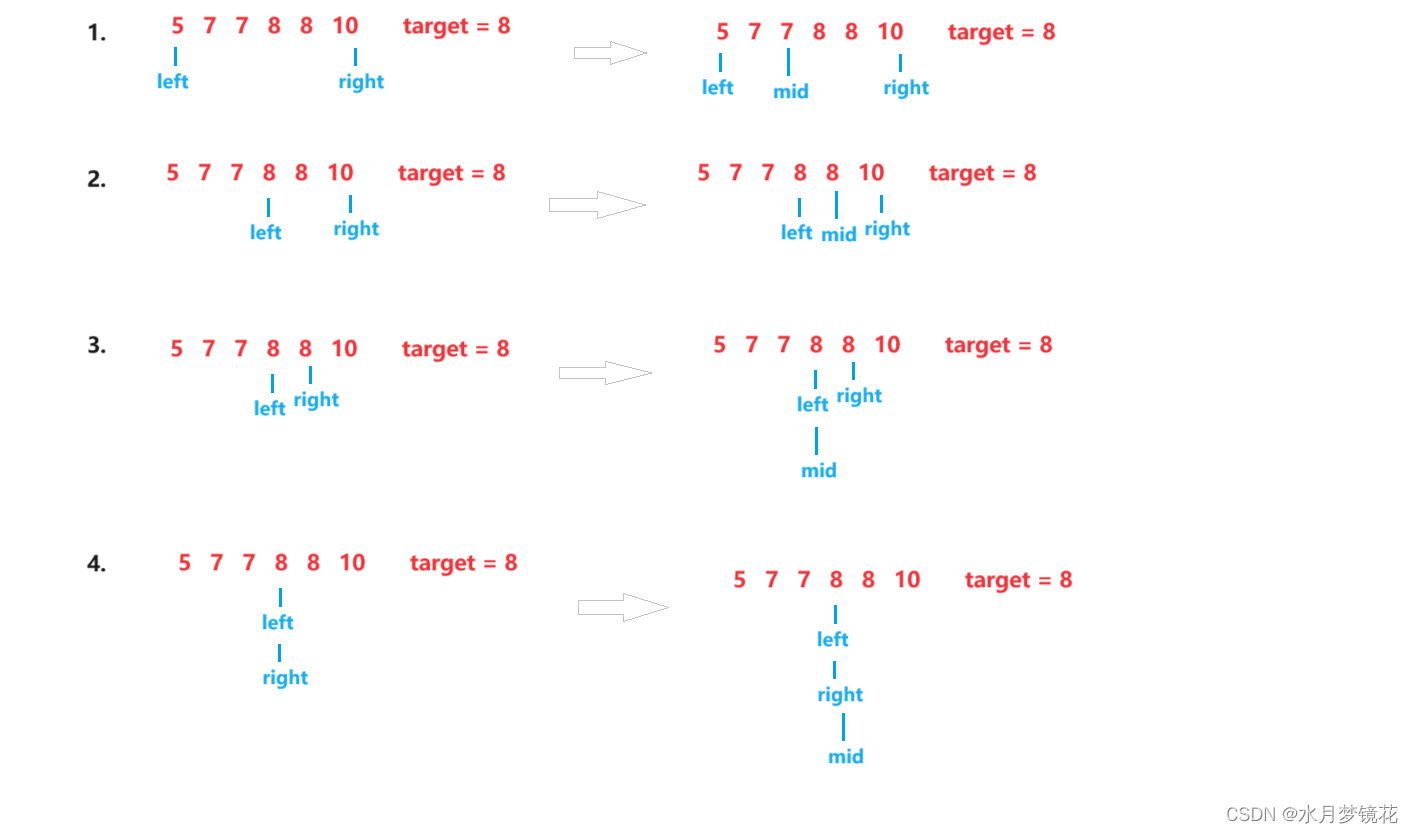
如上图4所示，nums[mid] >= target，right = mid。此时right依然与left指向同一个元素。

• 求mid的操作
  向下取整：mid = left + (right - left)/2 向上取整：mid = left + (right - left + 1)/2；二者主要区别在与如果区间[ left, right]中的元素个数是偶数时，向下取整取的是中间两个数中左边的数，向上取整取的是中间两个数中右边的数。
  此时查找区间左端点，求mid使用向上取整会导致死循环。
  

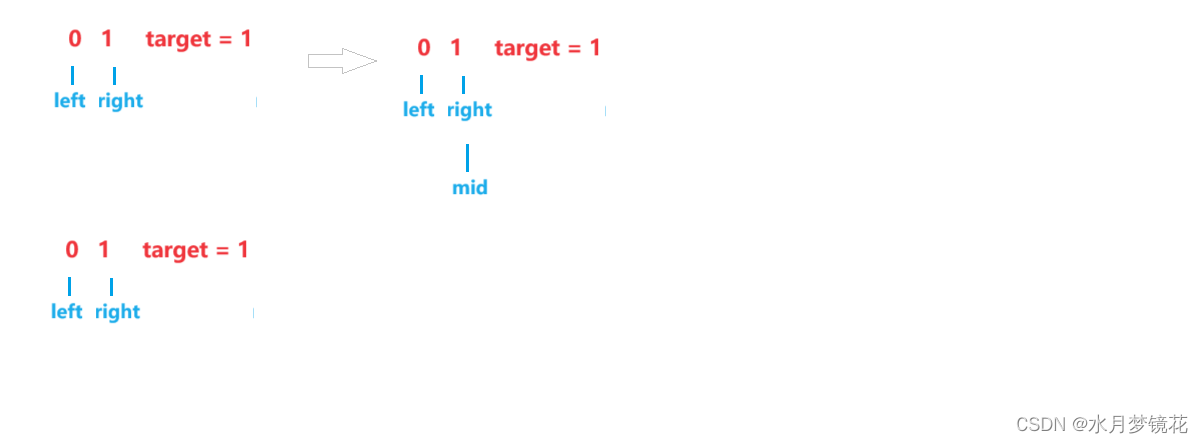
2. 查找区间右端点

查找区间右端点思路与查找区间左端点类似。
我们使用“二段性”发现示例一被target分成了两部分，小于等于target部分{5, 7, 7, 8, 8} 和大于target部分{10}。

如果点mid到小于等于target的部分，区间[ left, mid ] 这一区间都小于等于target，其中mid可能就是target区间的右端点，那么left = mid；
如果点mid到大于target的部分，区间[ mid, right ]这一区间都大于target，不可能是target区间的右端点，那么right= mid - 1；

---

细节处理：

• 循环条件：left < right， 理由与查找左端点使的循环条件相同，如果循环条件为left <= right会死循环
  
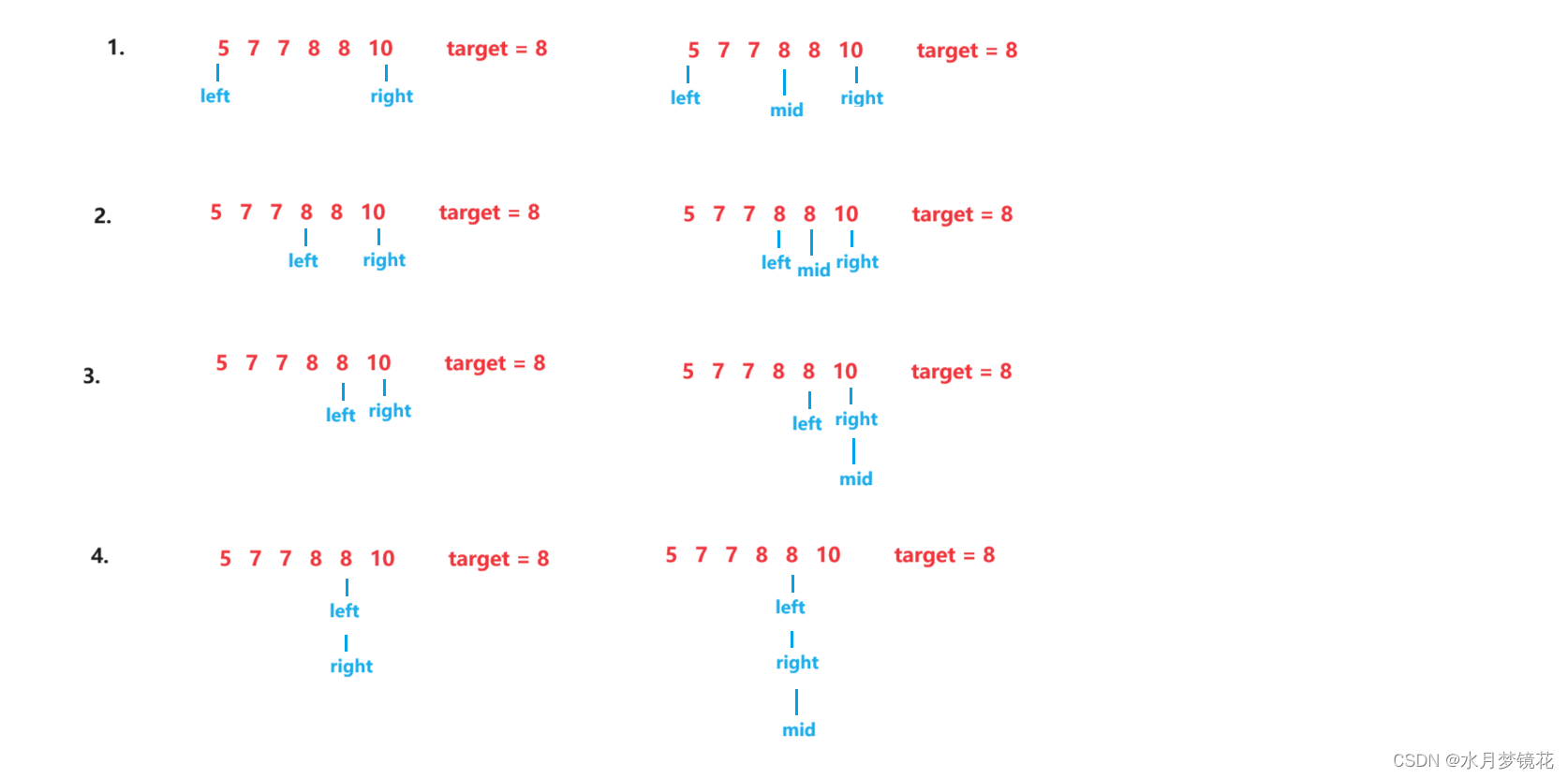
  如上图4所示，nums[mid] <= target，left = mid， 此时left依然与right指向同一个元素。

• 求mid的操作，这里就要用向上取整的方法 mid = left + (right - left + 1)/2
  此处查找区间右端点，如果使用向下取整会导致死循环
  

三、代码实现

两次二分查找分别查找左右端点

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {vector<int> ret({-1, -1});int n = nums.size();if(n == 0)return ret;int left = 0, right = n-1;// 查找左端点while(left < right){int mid = left + (right - left)/2;if(nums[mid] < target)left = mid+1;elseright = mid;}if(nums[right] == target)ret[0] = right;// 查找右端点left = 0, right = n-1;while(left < right){int mid = left + (right - left + 1)/2;if(nums[mid] > target)right = mid - 1;elseleft = mid;}if(nums[right] == target)ret[1] = right;return ret;}
};

---

总结

以上就是我对于在排序数组中查找元素的第一个和最后一个位置的理解。感谢支持！！！